Black Holes

If the final mass of a collapsing star is greater than 3-3.2 solar masses, the remnant collapses behind the horizon of a black hole.

(View Cosmos DVD 6, episode 9, on Flatland and curved space.)
Note that since mass is a scalar (having no directionality), it is a constant in every frame of reference.

For a black hole of mass M and angular momentum L, the horizon is a spherical surface located at a distance

r = (G M² + (G² M⁴ - c² L²)^1/2) / (M c²)

from the center of the black hole. This is a complicated function, so we will specialize for a moment to the (probably) unphysical case of a static black hole, which does not spin. Its horizon is then at

r = 2 G M / c²
= 2953 meters * M / M_solar
Note that this implies that G / c² is a conversion factor for converting mass to length.

The escape velocity necessary to escape the gravitational pull of a black hole gets larger as you get closer to the horizon. Using this expression for r, the escape velocity at the horizon is

ev = (2 G M / r)^1/2
= c

which is consistent with our notions

of nothing (particularly light) being able to escape from inside the horizon of a black hole, and
all light cones are tangent to the horizon of a black hole.

The surface gravity at the horizon is

g = c⁴ / (4 G M)
= 1.52 * 10¹³ m/s² / (M / M_solar)

For M = 2 M_solar, this is almost 2 million times the surface gravity of Sirius B, and 4 times that of the neutron star in the center of the Crab Nebula. But there is a caveat for the neutron star: it is a pulsar, so we know it spins, and therefore using our simplistic version of the equation for the horizon is not exactly a valid comparison. However, even though the pulsar is spinning 30 times each second, the angular momentum term is less than 0.03% of the mass term, so this result is very close.

Consider now the tidal acceleration experienced by a 2-meter object at the horizon:

G M / r² - G M / (r+2)²
= (c⁶ / (4 G M)) (c² + 2 G M) / (c² + G M)²

Since M is a multiple of M_solar, G M is much greater than c², and this reduces to approximately

c⁶ / (2 G² M²)
= 2 * 10¹⁰ / (M / M_solar)²

For M = 2 M_solar, this is about 5 * 10⁹ m/s². This means that our 2-meter object experiences a tidal acceleration over 500 million times Earth's surface gravity! But for M = 10⁶ M_solar, the tidal acceleration is 0.02 m/s²: unnoticeable.

It is expected that many if not most galaxies harbor a supermassive black hole in their cores, probably surrounded by an accretion disc, whose matter is accelerated to relativistic speeds and radiates tremendous amounts of energy as it falls into the horizon:

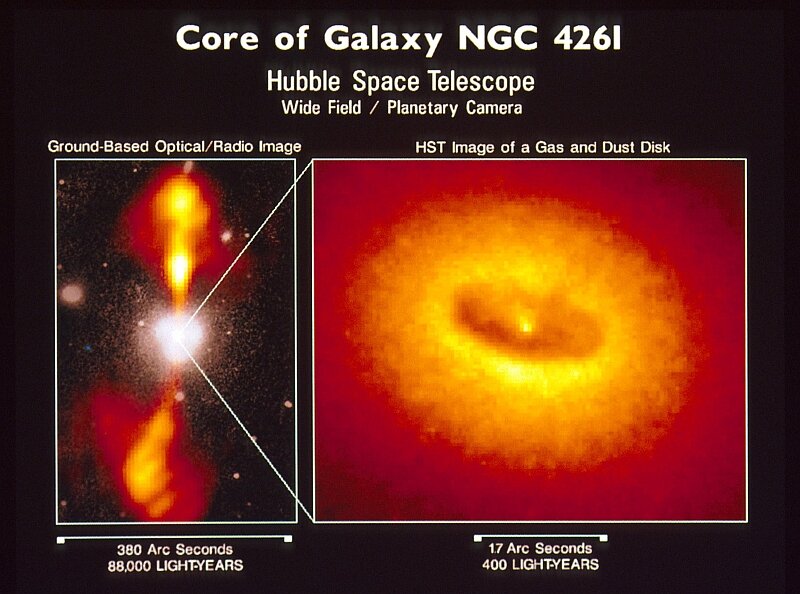
Accretion disc surrounding probable black hole in NGC 4261. (source)

Here is a movie of the crab pulsar (source). The disc-like disturbances around the pulsar and the accretion discs around the black holes are related in that the curvature of spacetime is essentially the same (except in magnitude) around all spinning masses. It is probable that most if not all of the violent events we see in the universe, from novae to gamma ray bursts, are powered by either

stellar collapse,
the accretion of matter onto a massive compact object like a white dwarf, neutron star or black hole, or
mergers of same.

Portfolio Exercise: Find a white dwarf other than Sirius B and a neutron star other than the one at the heart of the Crab Nebula, and compute the following: its density, the escape velocity at its surface, and its surface gravity. For the white dwarf, you will need to know its radius and mass; you will have to find its mass (which means it will probably have to be a binary companion), and you can compute its radius if you find its absolute magnitude and temperature. For the neutron star, your source will have to provide its mass and radius.
Now compute the horizon radius for a black hole of mass equal to the masses of the white dwarf and neutron star you found. Using that radius, compute the escape velocity and surface gravity of the "equivalent" black hole. Express all escape velocities in terms of the speed of light, and all surface gravities in terms of Earth's surface gravity (9.8 m/s²).

In this image from the Chandra X-ray Observatory, every object is thought to be a supermassive black hole:

Chandra Deep Field South. (source)

The image implies about 5000 in an area the size of the full moon, and a billion over the entire sky. Blue corresponds to higher energy, red to lower; the image took over 1944 hours to collect. The estimated distance is around 12 billion light-years from Earth, so they date from the early universe.

Curvature and Geodesics around a Black Hole

The hardest thing to conceptualize in General Relativity is how spacetime can be curved: how can something without substance have shape? With enough play time around a black hole, perhaps this can become clear, or at least clearer than it is now. Our black hole is electrically neutral, so it is described by only two parameters: its mass and its angular momentum. A collapsing star must have a mass "M" greater than (at least) 1.86 times the mass of the Sun to form a black hole, and its angular momentum "a" must be less than or equal to "M" for the black hole to have a horizon.

In the following applet, you can choose "M" and "a" for the black hole. You can also choose the initial position (relative to the horizon) and speed of a pair of probes, and their initial orbital direction: either azimuthal (around the "equator") or polar (along a "great circle" through the "north pole"). The "Replot" button starts the computations. Please be patient: each plot requires evaluation at over 3.5 million points! The "Replot" button will be labeled with ellipsis while the evaluation process is taking place.

You need a Java-capable browser to be able to use the applets. If they do not work with your Windows system, download the Java VM (Virtual Machine) for your version of Windows at the download section at java.sun.com.

The plot on the left is a 3-D plot showing the curvature of spacetime around the black hole, and the paths of the probes, which follow geodesics. The Geodesic Equations describe the path of any object whose own mass is negligible compared to the mass of the black hole (including light rays). The equations become very "stiff" near the horizon, so the last segment or two of the geodesic plots may not be smooth. The curvature is measured by the Kretschmann Invariant. Spacetime is described by a metric, which literally tells how the measurement of intervals varies from event to event. The Kretschmann Invariant is an algebraic function of the metric and its derivatives, which measures the curvature in a way that does not depend on the coordinate system used to describe the metric.

The 3-D plot is colored magenta where the Kretschmann Invariant is positive, and cyan where it is negative. Where the plot appears blue or white, you are seeing positive regions behind negative ones, or vise versa. The axes on the three dimensional plot are not drawn inside the horizon of the black hole. The region inside the horizon on the 3-D plot does not appear to be completely black because you are seeing it through some nonzero values of the invariant. The plot scale automatically changes so that the width of the plot is four times the radius of the horizon assuming "a" is 0. To zoom, turn the scroll wheel; to change the perspective, drag the mouse across the window.

The applet also provides a two dimensional plot (on the right) of time vs. position of the geodesics. The axes menus allow you to control the two dimensional plot. The origin of this plot is (0, 0) except when plotting radial distance, when it is (horizon radius, 0). The coordinates of the upper right hand corner are determined by the maximum values begin plotted (given in the "Final conditions" window at the bottom of the applet). For the polar and azimuthal angles, the right hand edge is at π/2 and 2 π, respectively. The polar plot includes a yellow line which marks the value of the polar angle where the curvature is zero at the horizon.

Things to try...

Lower the initial speed of the probes to 50% of the speed of light. This is less than the escape velocity and so the probes cross the horizon; but when? By default, the 2-D graph shows radial distance versus proper time (which is the time the probes measure). You can see that the probes cross the horizon in a finite amount of time, and the "Final conditions" data indicates that it is a very short time indeed. But if you choose "asymptotic time" for the 2-D vertical axis, a very different graph appears. We see that from the point of view of an observer "at infinity", the probes never cross the horizon but only approach it asymptotically. This is an eloquent indication that the coordinates we use to make measurements far from the black hole do not have the expected meaning in the region near the horizon.

You can see that changing "M" is only interesting if "a" is nonzero; this is because the applet automatically changes scale with "M". You can also see that "M" must be small and "a" must be a significant fraction of "M" before the plot changes substantially. This is a physical consequence of the spacetime metric around the hole.

Start the probes in a polar orbit with "a" = 1 (an extremal black hole); observe that near the horizon, in the region called the ergosphere, the angular momentum of the black hole "drags" the probes in the direction of the black hole's rotation. This is called frame dragging.
Note that as "a" increases, regions of "negative curvature" appear at the poles. What can this mean physically? The paths of the polar geodesics indicate that the regions of "negative curvature" correspond to centrifugal barriers.

Vary the initial position and speed to see how the escape velocity depends on the initial position. (You have found the escape velocity when the 2-D radial distance plot for the inner probe is a vertical line, or leans just slightly to the right.) Do this first for a = 0 and both large and small masses. Then set a = .9 M and do the same. Does the escape velocity depend on the mass? Does it matter whether the probes follow an azimuthal or polar orbit?
We found that the escape velocity at the horizon is the speed of light. Yet you may have noticed that even when starting the probes from a distance, at almost the speed of light, sometimes they enter the horizon. While it is true that the Newtonian escape velocity is the speed of light at the horizon, Einstein's General Relativity includes additional effects which imply that there is a region around the black hole for which there are no circular orbits. Since our probes start in a direction tangent to a circle around the black hole, in that region they must fall in!

We have really cheated a bit here for dramatic effect: we really don't need a black hole to see the same effects. The Kerr metric used in this applet describes spacetime around any isolated, compact rotating massive object. So the same effects, albeit much less pronounced, can in principle be measured around our Sun, or even around the Earth or the Moon.

Portfolio Exercise: Using the applet, vary the initial position and speed to see how the escape velocity depends on distance from the horizon. Do this first for a = 0 and masses of 2, 2000 and 2000000 M_solar. Then set a = .9 M and do the same. Does the escape velocity depend on the mass? Does it matter whether the probes follow an azimuthal or polar orbit?

Falling in...

The surface of the future light cone is where a particle could be if it travels at the speed of light, and the interior of the cone is where it could be if it travels more slowly. Therefore photons are destined to stay on the surface of their light cones and massive particles are destined to stay in the interior of their light cones.

Contrary to what you might have heard, this means that you will indeed expire when you cross the horizon of a black hole. Assuming you cross feet first, the future light cone of your feet is pointing into the center of the black hole, so no nerve impulses can reach your head from there. When your heart crosses, no blood can flow from it to your head. And when your head crosses the horizon, the parts of your brain cannot communicate with each other and your consciousness ceases.

Please send comments or suggestions to the author.