Cosmic Microwave Background Radiation

After collecting seven years of data from the Wilkinson Microwave Anisotropy Probe (WMAP), the WMAP Science Team released this image of the Cosmic Microwave Background Radiation (CMBR):

7 year data from the Wilkinson Microwave Anisotropy Probe. (source)

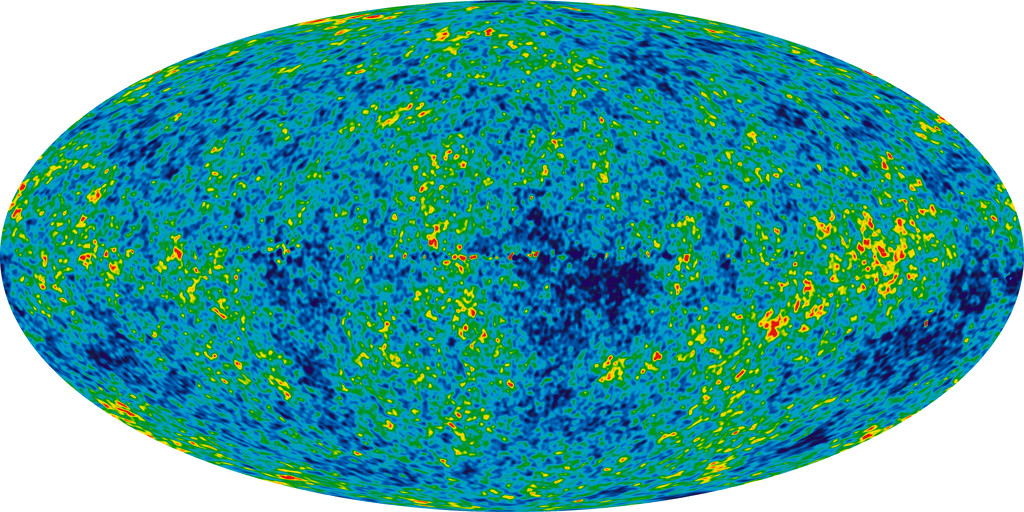
This image is a weighted linear combination of data in five radio frequency bands (23, 33, 41, 61 and 94 GHz) which minimizes the foreground contamination from the Milky Way. It is a snapshot of the photosphere or last scattering surface: our view of the universe when it first became transparent to electromagnetic radiation. The color scale in this image corresponds to temperatures of from 2.7248 to 2.7252 K (blue to red). This represents a deviation from perfect isotropy of one part in 13625.

Note that the last scattering surface depends on both the time of decoupling and the place and time of observation. The expansion of the universe changes the distance to the last scattering surface, and the passage of time increases our horizon, so we see more of the universe at decoupling as time passes.

The minute deviations from perfect isotropy in the CMBR tells us that there were small inhomogeneities in the plasma:

dark matter density fluctuations created small "pockets" of gravitational attraction into which baryons fell;
opposing that gravitational infall was the radiation pressure, and these opposing forces caused the plasma to oscillate;
during the radiation-dominated era, the fluctuations grew with time until the length scale of the fluctuations exceeded the horizon size (the distance light can travel during "one" fluctuation);
during the matter-dominated era, the fluctuations grew more slowly;
at decoupling, fluctuations were damped at all scales less than about 10 Mpc (so dark matter is required for galaxy formation);
the density fluctuations froze out when the universe became dominated by dark-energy.

These oscillations occurred at different length scales and left their imprint on the CMBR we observe today. Of course, those imprints have been modified by the expanding universe, and by other factors we have yet to discuss.

By comparing the CMBR temperatures at different angles, we can construct the power spectrum: a measure of the correlations between temperature as a function of angle.

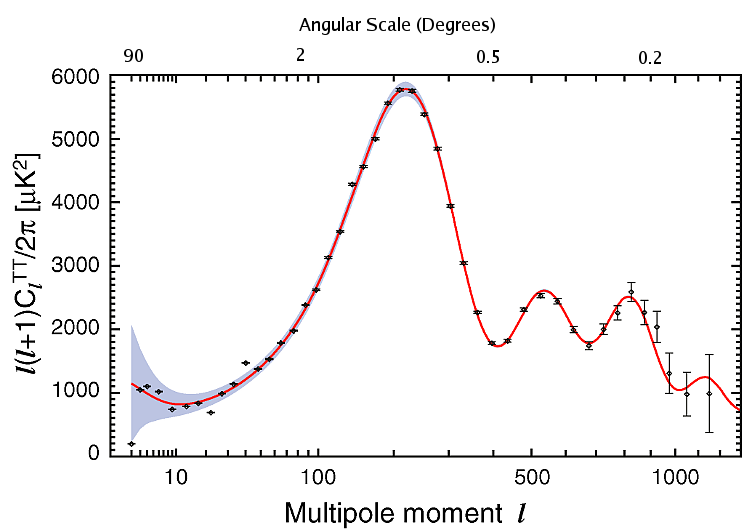
The power spectrum which best fits the 7-year WMAP data. (source)

The horizontal scale is the multipole moment, denoted l; the angular scale is actually π/l, so larger values of l denote smaller angles. The vertical scale is the temperature correlation function C_l, multiplied by l(l+1)/2π, and is measured in μK², or (10^-6K)². The blue region represents the range of data values within one standard deviation of the fit line.

The peaks in the power spectrum are called acoustic peaks, and indicate the length scales of the oscillations in the plasma before the temperature fluctuations froze out in the last scattering surface (at decoupling). The height and positioning of the peaks are influenced by a number of cosmological parameters. We will focus on the following:

Ω_b - additional baryon mass provides additional gravitational instability and increases the amplitudes (sizes) of the acoustic peaks - if Ω_b is a larger fraction of Ω_M, there is more inertia and the speed of sound in the plasma is smaller; this can make the sound horizon smaller (the region reachable by a given oscillation) and therefore the acoustic peaks occur at smaller scales

Ω_CDM - increases gravitational density fluctuations

Ω_vac - changes transition to dark energy-domination; at that time, density perturbations cease growing - if Ω_vac is larger, structures spread out more

τ_optical - after the last scattering surface freezes out (τ_optical = 1), matter structures begin to form in the early universe; when the first stars begin burning, much of the universe is re-ionized (from around z=10.7 until about z=6; τ_optical < 1); this is the optical depth at (time of) re-ionization - the re-ionization smooths out temperature fluctuations (earlier re-ionization produces more smoothing)

In addition, any parameter which affects k (primarily the Ωs) changes the angular scales we observe. Photons of the CMBR follow geodesics; the Geodesic Equations for the FRW metric tell us that the rate an angle changes is inversely proportional to the square of the scale factor. From the graphs above, we can see that smaller values of k cause the power spectrum to shift to higher values of l.

Note that the length scales corresponding to the acoustic peaks should correlate with the distances between large structures in the universe. Survey results have recently begun to confirm that expectation.

Comparing CMBFAST Results

We can use CMBFAST to explore regions of the space of possible cosmological parameters. The following applet will allow an easy comparison of the effects of various parameter values with the current best fit to the data. When you run CMBFAST, use the default parameter values for everything except the parameter(s) you have been assigned. Using CMBFAST, we can investigate the following:

the effects of altering the ratio of Ω_b to Ω_CDM without changing Ω_M;
the effects of changing the ratio of Ω_vac to Ω_M;
the effects of making Ω > 1 or < 1 without changing the ratio of Ω_b to Ω_CDM to Ω_vac, and
the effects of varying the optical depth.

After you run CMBFAST (which may take a few minutes), your results will be returned to you. Look for the number on the "Output Files" (ie., "02036736" in "cmb_02036736.fcl"). Enter that number in the applet below and it will load the power spectrum data and plot it. Each time you enter a different number, it will be plotted in a different color (from red to violet). The best fit plot is plotted in black.

You need a Java-capable browser to be able to use the applets. If they do not work with your Windows system, download the Java VM (Virtual Machine) for your version of Windows at the download section at java.sun.com.

We have ignored changes in the temperature anisotropy due to gravitational lensing. We have also ignored ionization from early hot clusters, and gravitational red shifting from the galaxy foreground (between us and the last scattering surface). Finally, all of our deliberations are strictly with the temperature anisotropies; there are also polarization anisotropies: deviations in the electric field and magnetic field directions in the CMBR. These promise to be important sources of information in future studies.

Portfolio Exercise: Using CMBFAST and the comparison applet, perform the 4 investigations listed above the applet. Do at least 4 trials for each investigation. Be sure that Omega_b is greater than 0 for each trial.
Capture images of each of the comparison plots for the 4 investigations, and annotate them, describing which plots belong to which parameter values.
What is the relationship between the results of investigation number 3 and the geometry of the universe?
Include all 4 in your portfolio.
The Planck Collaboration has recently released data from their first 15.5 months which estimate the Hubble parameter (H₀) at 67.15 km/s/Mpc, Ω_b at 0.049, Ω_CDM at .268 and Ω_vac at .683. Run CMBFAST with this profile and compare it to the others. Include it in your portfolio.

The Sunyaev-Zel'dovich effect

In a galaxy cluster, the spaces between galaxies is filled with hot gas. When photons from the CMBR interact with that gas, they pick up additional energy. This results in "holes" in the CMBR:

A hole in the CMBR around cluster RX J1347.5-1145. (source)

Here, blue represents the CMBR.

An Overview of Large-scale Structure Formation

This subject is relatively young, but we can build up what seems to be a reasonable picture as follows. Think of the formation of large-scale structures in the universe (galactic clusters, voids, etc.) as being a result of the merging of dark matter halos:

expansion of the universe causes under-dense regions to grow, forming voids;
voids are separated by sheets;
filaments form where sheets meet;
nodes form where filaments intersect;
the nodes correspond to cluster halos (interesting note: these halos tend to be triaxial ellipsoids);
as the universe continues to expand, the process builds structure from the bottom up: halos merge, accrete.

At re-ionization, the speed of sound was about 10 km/s, so halos with escape speeds less than that (around 10⁸ M_solar) didn't form stars (the gas would not fall into the halos).

Star formation drove gas out of the galactic halos (accounting for the presence of heavy elements in the intracluster medium); this process was aided by ram pressure as the galaxies moved through the intracluster medium.

Please send comments or suggestions to the author.