Nuclear Reactions

The primary source of the Sun's power output is the proton-proton chain:

(γ denotes a photon.) The first two of these reactions occurs twice for each occurrence of the third reaction.

In these nuclear reactions, the difference between the masses of the products and reactants can be used to compute the energy released by using
energy = mass * c2
Most people think of this as "converting matter into energy". Since energy is a quality of matter, and not really a separate entity, it is better to think of this process in terms of the constituent quarks of the protons and neutrons involved. Then we can see that each reactant has an energy content associated with the fact that they are bound states of particles which are electrically as well as strongly interacting. The product has a different binding energy, and the fusion process liberates the difference as gamma rays (with electromagnetic energy) and thermal energy of motion. The energy of any neutrinos which are produced is usually included as part of the energy released, because the neutrino has a very small and not very accurately measured mass in comparison with the other particles.
The mass of a proton (1H) is 1.673 * 10-27 kg; the mass of a Helium nucleus (4He) is 6.647 * 10-27 kg, and the mass of a positron (e+) is 9.109 * 10-31 kg. The energy released in neutrinos (νe) and gamma rays (γ) is then
E = (4 * 1.673 * 10-27 - 6.647 * 10-27 - 2 * 9.109 * 10-31) * (3 * 108)2
= 3.881 * 10-12 J

(= 24.225 MeV)

Using the solar constant (1365 W/m2) as the energy flux and 1 AU as the distance in the equation below, we can compute the luminosity of the Sun, obtaining LS = 3.84 * 1026 W. Dividing the luminosity by the energy per reaction gives the number of reactions per second, 9.92 * 1037. Since each reaction consumes 4 protons, the rate of Hydrogen consumption is
9.92 * 1037 * 4 * 1.673 * 10-27
= 6.64 * 1011 kg / s.
The photons released in these reactions are gamma rays, but the bulk of the electromagnetic radiation leaving the surface of the Sun is in the visible spectrum. The average travel distance (mean free path) between collisions for a photon in the center of the Sun is about 1 cm. On average, each photon leaving the surface has interacted with matter about 1021 times since being emitted in the core. Since many of these interactions involve the absorption and re-emission of the photon, the photons emitted at the surface are really distant ancestors of the ones created during fusion. Most interactions involve some energy loss (they are "inelastic"), and this accounts for the shift in spectrum from gamma to visible. The average time for a photon to travel to the surface from the core is
1021 * .01 m / c = 33 billion seconds
or over a thousand years.

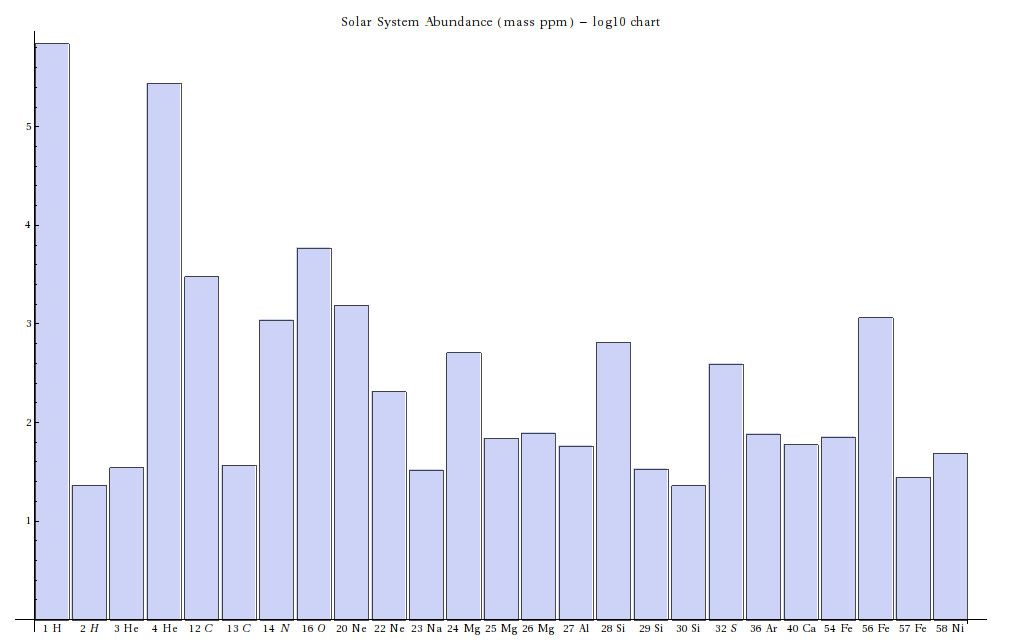
In the following list of nuclear reactions occurring in stars, numbers in parentheses are approximate energy yields in MeV; negative values indicate additional energy is required to make these reactions occur. Note that these are not all of the possible reactions; any reaction which conserves energy, momentum, angular momentum, electric charge, baryon number and lepton number can occur. Each reaction occurs with different frequency based on how much energy is required to overcome the electric repulsion between nuclei before the strong force takes over.

Note that baryon number conservation accounts for the drop in the number of nuclei available to fuse. For instance, it takes 56 1H to (eventually) make just one 56Fe.
The following masses (in atomic mass units (amu); 1 amu = 1.66055 * 10-27 kg) will enable you to compute more accurate energy yields from these reactions.

n1.008714N13.995432S31.9633
1H1.0072515N14.996336Ar35.9576
2H2.0135515O14.998740Ca39.9516
3He3.014916O15.990544Ti43.9476
4He4.001520Ne19.986948Cr47.9408
8Be8.0031123Na22.983852Fe51.9338
12C11.996723Mg22.987556Fe55.9206
13C13.000124Mg23.978456Co55.925
13N13.001928Si27.97956Ni55.9267

You can find the atomic numbers of these atoms from the Periodic Table of the Elements.

Neutron capture can form atoms with atomic masses larger than Iron, for instance in the series of processes:
56Fe + 1n -> 57Fe

57Fe + 1n -> 58Fe

58Fe + 1n -> 59Fe

59Fe -> 59Co + e- + νe

59Co + 1n -> 60Co

60Co -> 60Ni + e- + νe

Observation of the merger of two neutron stars on August 17, 2017 seems to indicate that such mergers may be the primary source of heavy elements in the universe.
But nuclear fusion ends with Iron production. This is because 56Fe fusion is an endothermic process: it takes more energy than it releases. For instance,
56Fe + 56Fe -> 112Te
requires over 44 MeV to take place. While we have seen several such reactions above, they have proceeded because excess energy is available in the active core of the star. Once an Iron core forms, there are no reactions available to provide the additional energy necessary for Iron fusion to occur.
It is often said that 56Fe is the most stable nucleus. A nucleus is said to be stable if its energy per baryon is a minimum for its atomic number. Unstable nuclei undergo radioactive decay, emitting Helium nuclei (alpha decay, which heavier nuclei often do because they lose energy quicker), electrons or positrons (beta decay, accompanied by neutrinos), or photons (gamma decay, if nothing else is allowed). The reactions marked with an asterisk above are all beta decays. Fusion stops with Iron because 56Fe has the lowest energy per baryon of any nucleus (-8.8 MeV / baryon).
Portfolio Exercise: For each of the fusion reactions above, compute the energy yield.
This table shows the solar system abundances of a number of elements and isotopes (the vertical axis is log base 10, so, for instance, since 4He ≈ 3He + 4, there is about 104 = 10,000 times more 4He than 3He):

©2018, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.