Stellar Populations

Here we are interested in all stars, and in classifying them as an aid to understanding the physics behind them.

Spectral Classes and Effective Temperatures

Spectral classes were originally defined using visual cues from spectra. We will define them in terms of effective surface temperature, using the letters "O", "B", "A", "F", "G", "K" and "M" (from hottest to coolest) and subdivide each main class into 10 subclasses, labeled by the digits 0 through 9 (again, hottest to coolest). The following plot gives the most likely effective temperature for each spectral class:

Effective temperature vs. spectral class; red/orange = main sequence, red = giants, blue = supergiants.

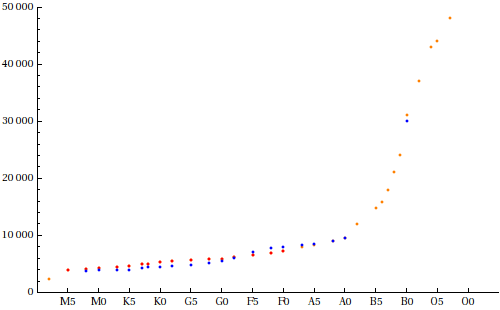
Using our temperature of 9300 K from the Spectrum Viewer, we see that 108 Virginis is likely close to a class A1 (interpolating between the temperatures for A0 and A2 in the graph).

Magnitude, Luminosity Classes and Spectral Classes

If we know the luminosity, or the apparent magnitude and the distance to the star, we can compute the absolute magnitude using one of the equations

absolute magnitude = 4.83 - 2.5 * log₁₀ luminosity_solar
absolute magnitude = apparent magnitude + 5 - 5 * log₁₀ distance_pc

For 108 Virginis, at a distance of 188.3 parsecs and a luminosity of 110 L_solar, we obtain an absolute magnitude

M = 4.83 - 2.5 * log₁₀ 110 = - 0.27

and an apparent magnitude of

m = - 0.27 - 5 + 5 * log ₁₀ 188.3 = 6.1

Note that because of our underestimate of the luminosity, M is larger (less negative) than it should be, and m is also larger than it should be. Here the error is even less than in our radius calculation because the log function increases more slowly than the square root.

Standard luminosity classes are

Ia - Bright Supergiants
Ib - Supergiants
II - Bright Giants
III - Giants
IV - Subgiants
V - Dwarfs (including Main Sequence Stars)

A spectral class beginning with "D" indicates a degenerate star, or white dwarf: a star which has collapsed to a small, hot cinder after fusion processes have stopped. Additional designations include "e" (has emission lines), "n" (has diffuse lines), "p" (has a peculiar spectrum; even physicists don't understand it all yet!), "s" (has sharp lines), and "v" (variable star).

The following table relates the absolute magnitude to the luminosity class for each spectral class (the magnitudes given are the most likely values for each class):

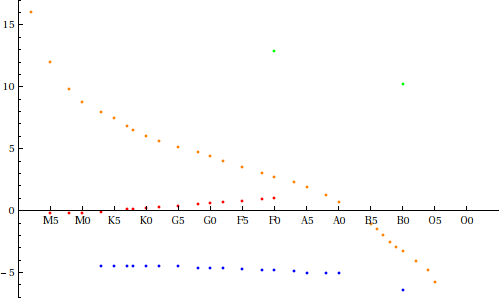
Absolute magnitude vs. spectral class; orange = main sequence, red = giants, blue = supergiants, green = white dwarfs.

Using the estimated class A1 for 108 Virginis, we see that it could conceivably be a main sequence star, a supergiant, or a white dwarf. Given an absolute magnitude of -0.27, it is much more likely that it is a main sequence star.

Using SIMBAD, you can look up the accepted spectral class for 108 Virginis. You will find it listed as "B9.5V". Our choice of A1 is very close to B9.5, and the "V" indicates a main sequence star, so our choice of luminosity class was correct.

Portfolio Exercise: Using the information you have collected so far, assign a spectral class to each of your stars from the spectra portfolio exercises.
For each star, compute the absolute and apparent magnitudes. Assign a luminosity class to each star.
Look each star up on SIMBAD. Comment on your success rate.

The Hertzsprung-Russell Diagram

Suppose you could take a picture of every person on Earth at a given instant of time. Armed only with that picture, you must find a model that explains the human life cycle, from conception to death. The Hertzsprung-Russell Diagram is like that picture, and with it we can learn some things about the lives of stars. Note that it is like a mirror image of the graph above:

A Hertzsprung-Russell Diagram. (source)

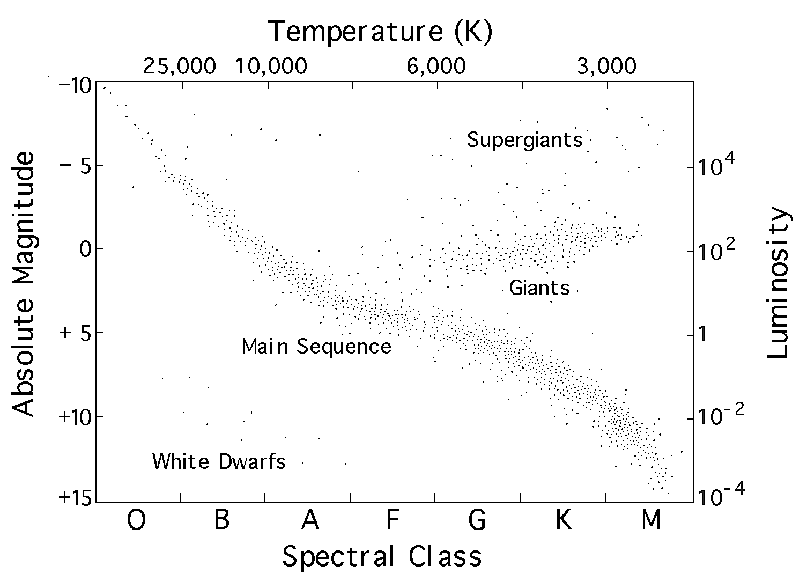
The position of a star on the main sequence (the line from upper left to lower right) is determined by its mass. Main sequence stars of spectral type G0 are about 1 M_solar, while those of type B0 are about 15 M_solar (stars begin their main sequence lives with masses varying from 0.07 to about 200 M_solar (source)). Almost half of the stars in the neighborhood of our Sun have a mass less than about a third of the Sun's; about one in 300 of the neighborhood stars have a mass in excess of 8 M_solar.
The main sequence ends at about 2100 K. Below that temperature are larger brown dwarfs: "failed" stars, which have insufficient mass to initiate fusion.
Straight diagonal lines parallel to the tangent at the center of the main sequence correspond roughly to lines of equal radius. Our B0 main sequence star has a radius around 10 R_solar. The spacing of these lines of equal radius is roughly logarithmic.

The first thing to notice is that by far, most of the data points lie on the main sequence. Since we are looking at a population of stars at a different time in each star's life, that tells us that stars spend most of their lives on the main sequence. As a consequence, the (super)giant and white dwarf regions of the diagram must represent stars at various stages near the ends of their lives (assuming that most of the data points represent stars and not protostars).

Another thing to notice is that the white dwarf region of the diagram is distributed over a relatively wide range of luminosities and temperatures. This means that knowledge of temperature does not translate as easily into knowledge about luminosity as it does with main sequence stars. At first glance one might be tempted to say the same thing about the giant and supergiant regions, but because they represent definite paths in the life cycles of those stars, and the stars themselves are much larger and brighter, they do not represent so much of a problem.

We can learn much about the populations of stars in a galaxy like ours by looking statistically at the stars we know best: those closest to us. Using a recent survey (source), we have culled spectral class, apparent magnitude and parallax data for 3633 stars near the Sun. This data is available in an Excel spreadsheet. Using the parallax data, you can compute each star's distance from Earth as

distance_pc = 1000 / parallax_mas

From the relation

absolute magnitude = apparent magnitude + 5 - 5 * log₁₀ distance_pc

you can then compute each star's absolute magnitude. The absolute magnitude can be used to determine the luminosity from the relation

absolute magnitude = 4.83 - 2.5 * log₁₀ luminosity_solar

luminosity = 10^{(4.83 - absolute magnitude) / 2.5}

Assuming that luminosity is approximately equal to mass^3.5, you can then compute each star's mass as

mass_solar = luminosity_solar^(1/3.5)

Portfolio Exercise: Create a histogram of the spectral classes of this population of stars. Omit stars with spectral classes other than O, B, A, F, G, K or M, and stars with a range of possible classes. Include stars of all subclasses in the main class (ie., count M and M1 through M9.5 all as class M). Note the percentage of stars for which there is no subclass; what does this say about the difficulty of stellar classification?
Create a histogram of the known luminosity classes of this population of stars. Omit stars with luminosity classes other than I-V and D/SD (white dwarf and sub-dwarf, sometimes designated VII and VI, respectively). Note the percentage of stars for which there is no luminosity class; what does this say about the difficulty of luminosity classification?
Create a histogram of the masses of this population of stars. What is the average mass to luminosity ratio (in solar units)?

Binaries and Stellar Clusters

Approximately 75% of all stars are members of binary systems; the vast majority of these systems are primordial: they were formed as a binary pair, as opposed to dynamical capture of one star by another.

Stellar clusters are groups of stars which are gravitationally bound (possibly very loosely). Clusters can be

open, or galactic clusters: these are small associations of young stars (100 to 10,000), usually found in the galactic plane; as the gas clouds which gave them birth are blown away by stellar winds and/or ionizing radiation, the resulting loss of mass allows most to eventually disperse; all stars begin life as cluster members;

globular clusters: larger (10,000 to millions of stars), older, and usually found in the galactic halo, these contain little interstellar gas and usually have very dense centers; the average star has orbited that center on the order of 10,000 times since it was formed.

	The Pleiades (M 45), an open cluster.	source
	NGC 604, near M33, a young cluster still within its birth cloud.	source
	NGC 602, where radiation from young cluster members is triggering more star formation.	source
	Globular cluster M 80, with many old red giants and a few blue giants, possibly the result of stellar mergers.	source
	Globular cluster M 9, with fewer red giants.	source
	Globular cluster M 53, with an unusual number of blue giamts ("stragglers").	source

Please send comments or suggestions to the author.