
You can choose where you are from the first pop-up menu, and what you are looking at from the second. If the two are not the same, you can choose the latitude where you are; if they are the same, the latitude scroll bar becomes a "z" scroll bar, allowing you to view the body from above or below. When the "from" and "viewing" targets are different and you are viewing from a planet, you may choose either geocentric or heliocentric views. The applet begins in "heliocentric" mode, meaning you are looking at the sky in flat projection, with the latitude relative to the plane of the Solar System; as you change the date and time, or animate, you will always be at the first object, viewing the second object. In "geocentric" mode, you are viewing from the first object, but seeing the sky in polar projection (as if you were standing on the Earth).The date and time scroll bars allow you to see the sky at a specific date and time. You can also draw and erase line-of-sight markers using the appropriate buttons, but they are only drawn when the "from" and "viewing" targets are the same.
When the "from" and "viewing" targets are different, the coordinates represent angles and the lattice lines are drawn every 15 degrees. When the "from" and "viewing" targets are the same, the coordinates are distance. All times are Universal Time.
It's a little complicated, but it's a powerful little program. Even the author hasn't fully explored its possibilities...
You can use it to explore the following phenomena:
From Earth, view Alpha Centauri in Heliocentric mode and press the "Animate" button twice; you will see the Sun, the Moon and the planets move along the center line: the plane of the Solar System, also called the ecliptic; pressing the "animate" button one more time stops the animation.
In Geocentric mode, at a latitude of 39 degrees, push the "Hour" button repeatedly; observe the motion of the planets and stars as they "rise" in the East and "set" in the West.Then, press the "Day" button repeatedly and observe the changes in the midnight sky as the days of a month progress; in Heliocentric mode, from Earth view the Earth and press the "Magnify" button; see how the phases of the Moon change as you repeatedly press the "Day" button.
Reload the page; in Geocentric mode, at a latitude of 39 degrees, push the "Magnify" button and set the hour to 12; then observe the changes in the position of the noonday Sun as you repeatedly press the "Month" button; the path over the course of a year is called an analemma.
Reload the page; from the Sun, view the Sun; set the z control to 24 and push the "Animate" button twice; observe the relative positions of the planets (through Saturn) as they orbit the Sun.
Reload the page; in Heliocentric mode, press the "Magnify" button, then press the "Animate" button twice and watch the Moon move in and out of the plane of the ecliptic; as the Moon moves in front of or behind the Sun, we observe partial or full eclipses based on where the Moon lies relative to the ecliptic.
From Earth, push the "Animate" button twice while viewing Betelgeuse on 6/1/00 (pay attention to Mercury) or 10/1/07 (Mars); or view Fomalhaut on 7/1/03 (Mars), or M48 on 8/1/05 (Mercury, then Mars, then Saturn).Now view Mars, set the date for 8/1/07 and alternately push the "Draw Marker" and "Month" buttons until 5/1/08. Then from the Sun view the Sun and set "z" to 4; the markers show how the position of Mars changes relative to the stars as Earth "laps" Mars.
Noon is defined as the time when the Sun is highest in the sky (at its zenith); a solar day is the time between two successive noons. A sidereal day is the time between two successive risings of any given star (other than the Sun).Reload the page; from Earth, view the Sun and push the "Draw Marker" button (nothing will appear yet); then view Altair and draw a new marker; then press the day button once and again draw two markers as before; finally, from the Sun view the Sun and set "z" to 3; since the two markers pointing to Altair are parallel, but the two pointing to the Sun are not, you can see that in 24 hours, due to the change in the position of the Earth as it rotates around the Sun, the position of the Sun changes relative to the stars; this causes the sidereal day to differ from the solar day.
A synodic month is the time between two full moons.Reload the page; from Earth, view the Earth and push the "Magnify" button; push the "Day" and "Hour" buttons until the Moon is aligned along one of the axes. Then set the time for 27.3 days (1 sidereal month) later and note the position of the Moon (the slight difference is due to the Earth's rotation around the Sun); then set the time for 2.2 days later than that (one synodic month since the first time) and note the position of the Moon, and that its phase is the same as it was 29.5 days earlier.

Here is a time-lapse sequence showing the orientation of the terminator between daylight and night on the Earth over the course of a full year.
Here is a time-lapse sequence of the Moon through a complete lunar cycle.
| Body | Perihelion | Aphelion | Ang. Diam. @ | Orbital | Orbital | Rotational | Axial Tilt |
|---|---|---|---|---|---|---|---|
| (AU) | (AU) | ca. (as) | Period (Yrs) | Inclination | Period (Days) | ||
| Sun | 1918 | 2.2 * 108 | 25.38 | 7.25 | |||
| Mercury | 0.3075 | 0.4667 | 13.03 | 0.241 | 7 | 58.65 | 0 |
| Venus | 0.718 | 0.728 | 65.44 | 0.615 | 3.39 | -243 | 177.3 |
| Earth | 0.983 | 1.017 | 1 | 5. * 10-5 | 0.9973 | 23.45 | |
| The Moon | 0.00243 | 0.00271 | 1968 | 0.075 | 5.145 | 27.32 | 6.68 |
| Mars | 1.381 | 1.666 | 25.73 | 1.881 | 1.8 | 1.026 | 25.19 |
| Phobos | 6.175 * 10-5 | 6.363 * 10-5 | 0.1047 | 8.731 * 10-4 | 1 | 1.026 | |
| Deimos | 1.567 * 10-4 | 1.569 * 10-4 | 0.05824 | 0.003456 | 1.8 | 1.026 | |
| Ceres | 2.549 | 2.9853 | 1.6658 | 4.6 | 10.58 | 0.379 | |
| Eros | 1.133 | 1.783 | 0.2022 | 1.76 | 10.83 | 0.2202 | |
| Gaspra | 1.8251 | 2.5929 | 0.0276 | 3.29 | 4.1 | 0.2942 | |
| Ida | 2.732 | 2.99 | 0.06385 | 4.84 | 1.14 | 0.1936 | |
| Mathilde | 1.9422 | 3.2082 | 0.08541 | 4.31 | 6.71 | 17.45 | |
| Vesta | 2.1506 | 2.5734 | 1.2517 | 3.63 | 7.14 | 0.2232 | |
| Jupiter | 4.952 | 5.455 | 50.1 | 11.86 | 1.305 | 0.4135 | 3.12 |
| Io | 0.00281 | 0.002832 | 1.2761 | 0.004844 | 0.04 | 1.769 | |
| Europa | 0.004445 | 0.004526 | 1.097 | 0.009723 | 0.47 | 3.551 | |
| Ganymede | 0.007138 | 0.007167 | 1.846 | 0.01959 | 0.21 | 7.155 | |
| Callisto | 0.0125 | 0.01268 | 1.684 | 0.04569 | 0.51 | 16.69 | |
| Saturn | 9.021 | 10.05 | 20.76 | 29.4 | 2.484 | 0.444 | 26.73 |
| Mimas | 0.001215 | 0.001265 | 0.06753 | 0.00258 | 1.53 | 0.9424 | |
| Enceladus | 0.001584 | 0.001598 | 0.0851 | 0.003751 | 0 | 1.37 | |
| Tethys | 0.00197 | 0.00197 | 0.1826 | 0.005169 | 1.86 | 1.888 | |
| Dione | 0.002517 | 0.002528 | 0.1929 | 0.007493 | 0.02 | 2.737 | |
| Rhea | 0.00352 | 0.003527 | 0.2632 | 0.01237 | 0.35 | 4.518 | |
| Titan | 0.007929 | 0.008406 | 0.8871 | 0.04366 | 0.33 | 15.95 | |
| Hyperion | 0.00887 | 0.01093 | 0.03062 | 0.0583 | 0.43 | 13 | (chaotic) |
| Iaepetus | 0.02313 | 0.02448 | 0.2474 | 0.2172 | 14.72 | 79.33 | |
| Uranus | 18.29 | 20.1 | 4.086 | 84.02 | 0.77 | -0.7196 | 97.86 |
| Miranda | 8.658 * 10-4 | 8.705 * 10-4 | 0.03769 | 0.00387 | 4.2 | 1.413 | |
| Ariel | 0.001272 | 0.001281 | 0.09246 | 0.0069 | 0.3 | 2.52 | |
| Titania | 0.00291 | 0.002923 | 0.126 | 0.02384 | 0.14 | 8.706 | |
| Neptune | 29.81 | 30.33 | 2.372 | 164.8 | 1.769 | 0.6712 | 29.58 |
| Triton | 0.002371 | 0.002371 | 0.1295 | -0.01609 | 157.3 | -5.877 |
("ca." stands for "closest approach".)
Since we telescopically measure only angular positions in the sky, we cannot measure perihelion and aphelion directly; we require an independent measurement of distance. This is done, for example, by radar ranging of Venus at closest approach. Thus the perihelion and aphelion values are actually computed and not directly observed. Planetary orbits are elliptical, and orbital parameters such as perihelion and aphelion are obtained by fitting careful measurements to elliptical orbits.
The data in the tables in this section come from NASA and NASA. There is an Excel spreadsheet available containing some of this information. It will serve as a starting point for your efforts to duplicate the conclusions below.
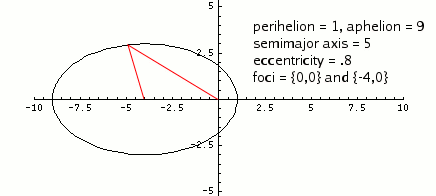
Using the above information and the equations
and
we can compute the following parameters:
| Body | a(AU) | Eccentricity | R(m) | R(Earth) |
|---|---|---|---|---|
| Sun | 1.62 * 109 | 6.955 * 108 | 109 | |
| Mercury | 0.3871 | 0.2056 | 2.44 * 106 | 0.3825 |
| Venus | 0.7233 | 0.0068 | 6.052 * 106 | 0.9488 |
| Earth | 1 | 0.01671 | 6.378 * 106 | 1 |
| The Moon | 0.00257 | 0.0549 | 1.734 * 106 | 0.2719 |
| Mars | 1.524 | 0.0934 | 3.397 * 106 | 0.5326 |
| Phobos | 6.269 * 10-5 | 0.015 | 1.3816 * 104 | 0.002166 |
| Deimos | 1.568 * 10-4 | 5. * 10-4 | 7688 | 0.001205 |
| Ceres | 2.767 | 0.0789 | 4.73 * 105 | 0.0742 |
| Eros | 1.458 | 0.2229 | 11001 | 0.001725 |
| Gaspra | 2.209 | 0.1738 | 8428 | 0.001321 |
| Ida | 2.861 | 0.0451 | 2.025 * 104 | 0.003175 |
| Mathilde | 2.646 | 0.266 | 3.265 * 104 | 0.005118 |
| Vesta | 2.362 | 0.0895 | 2.65 * 105 | 0.04155 |
| Jupiter | 5.203 | 0.04839 | 7.149 * 107 | 11.21 |
| Io | 0.002821 | 0.004 | 1.821 * 106 | 0.2855 |
| Europa | 0.004485 | 0.009 | 1.565 * 106 | 0.2454 |
| Ganymede | 0.007153 | 0.002 | 2.634 * 106 | 0.413 |
| Callisto | 0.01259 | 0.007 | 2.403 * 106 | 0.3768 |
| Saturn | 9.537 | 0.05415 | 6.027 * 107 | 9.449 |
| Mimas | 0.00124 | 0.0202 | 1.96 * 105 | 0.03073 |
| Enceladus | 0.001591 | 0.00452 | 2.47 * 105 | 0.03873 |
| Tethys | 0.00197 | 0 | 5.3 * 105 | 0.0831 |
| Dione | 0.002523 | 0.00223 | 5.6 * 105 | 0.0878 |
| Rhea | 0.003523 | 0.001 | 7.64 * 105 | 0.1198 |
| Titan | 0.008167 | 0.02919 | 2.575 * 106 | 0.4037 |
| Hyperion | 0.0099 | 0.104 | 8.878 * 104 | 0.01392 |
| Iaepetus | 0.02381 | 0.02828 | 7.18 * 105 | 0.1126 |
| Uranus | 19.19 | 0.04717 | 2.559 * 107 | 4.012 |
| Miranda | 8.681 * 10-4 | 0.0027 | 2.36 * 105 | 0.037 |
| Ariel | 0.001276 | 0.0034 | 5.79 * 105 | 0.09078 |
| Titania | 0.002916 | 0.0022 | 7.889 * 105 | 0.1237 |
| Neptune | 30.07 | 0.00859 | 2.476 * 107 | 3.883 |
| Triton | 0.002371 | 1.6 * 10-5 | 1.352 * 106 | 0.212 |
| Tempel 1 | 3103 | 4.865 * 10-4 | ||
| Wild 2 | 2750 | 4.312 * 10-4 |
Of course, a and ε are sufficient to describe any one of these orbits, but in order to understand how the planets are oriented with respect to each other we need 4 additional values:
Together these 6 values are called orbital elements. From them we can predict the past and future positions of any of the planets, to reasonable accuracy, within about 20 years of the time mentioned above. Beyond those dates, gravitational interactions between the planets must be taken into account.
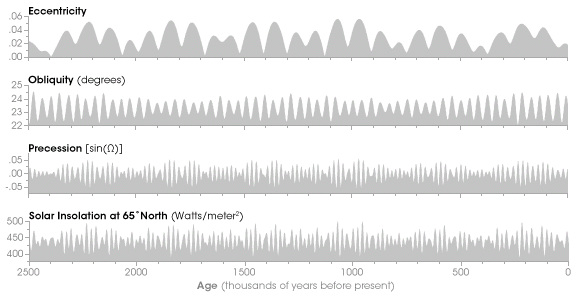
There are subtle variations in eccentricity and tilt which cause long term cycles in the amount of sunlight received in the northern hemisphere, and which drive cyclic climate change:
©2017, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
Portfolio Exercise:
Compute the following characteristics for each body in the table above: volume (in units of Earth's volume),
surface area (in units of Earth's surface area) and average orbital velocity (in km/hour). Include details on the
formulas used to compute the radius of each body.