Special Relativity is a theory of kinematics: it gives us a framework for describing the world, but it does not predict how the world will behave under any given conditions. What makes SR special is that it forces us to treat time as a relative of space: there is no separate space which we measure with meter sticks, and a separate time which we measure with clocks. There is only spacetime, and every measurement requires both a meter stick and a clock. And this presents a problem.
We are familiar with three spatial directions: you may think of them as "left-right", "up-down" and "in-out". A mathematician would perhaps give those directions labels; for instance, "x", "y" and "z". Our whole biology, and most especially our minds, are "wired" to understand life in "3-D": three spatial dimensions. But if time is an integral part of spacetime, and cannot be consistently divorced from it, spacetime must be "4-D": it must have four dimensions. And nothing in our biology is fit to understand four dimensions.
Consider a planet in a circular orbit around a star. We observe its motion one moment at a time; we can only "see" its previous motion in our memory, and we can only anticipate its future motion if we have studied hard enough. But our sensory experience occurs as a sequence of spatial observations:
A being who could see time in the same context as the spatial dimensions would see something entirely different. Since we know our orbiting planet is essentially motion in a plane, we can show you what this superior being observes by plotting time along the axis perpendicular to the plane of the orbit:
The "cylinder" along the time axis is the continuous view of the star, as the planet "spirals" in the "plane-time" view.
Of course, when the motion is truly three-dimensional, we cannot construct a static image of its movement in space and time. A mathematician would say that the embedding of a four-dimensional object in three dimensions is impossible. But all is not hopeless: there are tools which can help us. One such tool is the projection.
 | Gojira in the x-y plane; the z direction (in-out) has been projected out. | |
 | Gojira in the y-z plane; the x direction (left-right) has been projected out. | |
 | Gojira in the x-z plane; the y direction (up-down) has been projected out. | |
 | Using coordinates (r,ct), light moves along lines which form 45 degree diagonals with the axes. |
Whenever you take a picture, you are projecting a 3-D object into 2-D, and in the process you are ignoring the information in the third dimension. We are of course assuming here that you are not taking stereoscopic pictures, which allow your eyes to reconstruct the original 3-D object from a pair of 2-D images taken from slightly different positions.
But these photos have actually projected out another dimension: time. In them we see Gojira posing for the cameras of the paparazzi, but we have lost all of the information about what cities he may have demolished before or after the photos were taken. Every photograph is a 2-D projection of a 4-D object: it throws away information about an object that occupies three spatial dimensions and one temporal (timelike) dimension by depicting only two of the spatial directions, and freezing the object in an instant of time.
Since we often are concerned with the distances between objects, we often take the horizontal axis of our plot to be the distance from the origin of our coordinate system, and the vertical axis to be the time. In addition, we often take t=0 to be some significant event. The fact that some times are therefore negative simply indicates that the events at those times occurred before that significant event.
 | The world line (in red) of a planet orbiting a star in a perfectly circular orbit, with the star at the origin of our coordinate system. | |
 | The world line of a very eccentric comet (one which orbits its star in a highly elliptical orbit). |
Since the radius of a circle is a constant, the world line of the planet in the r-t plane is a straight vertical line. Both plots ignore any angular information about the respective world lines: we do not know in which direction either object lies at any point in time. That information has been lost in the projection. But in many cases the system has sufficient symmetry that the angular information is irrelevant. If we take either of these systems as isolated (perhaps hidden in a vast dust cloud which renders the rest of the universe invisible), the only preferred direction is the direction defined by the axis of rotation of the star. If we take that direction to be along the z axis (as is customary), the only piece of information missing in either plot is the inclination of the orbit: how tilted it is with respect to the z axis. If the cometary system is not isolated, we are also missing information about the direction of its orbital axis with respect to, say, the direction toward the center of the galaxy. But in many cases of interest, there is sufficient symmetry for a 2-D plot of world lines to be essentially complete.
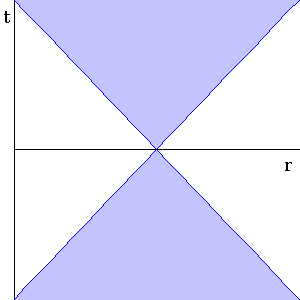
In this plot, the line going from lower left to upper right represents a ray of light moving away from the origin, while the line going from lower right to upper left represents a ray of light moving toward the origin. We call the region between those lines the light cone of the event at t=0 (where the light rays crossed). The (shaded) lower part is called the past light cone of the event and the (shaded) upper part is called the future light cone of the event.
The past light cone includes all events that could have influenced the event at t=0, and the future light cone includes all events that the event at t=0 could influence. Note that every event (every point on the r-t plane) has its own light cone.
If we plot the comet's world line with our new scale, it looks identical to the planet's. Its orbital motions are obscured because the speed of light is so fast that the scale has flattened out the variations in its orbital distances.
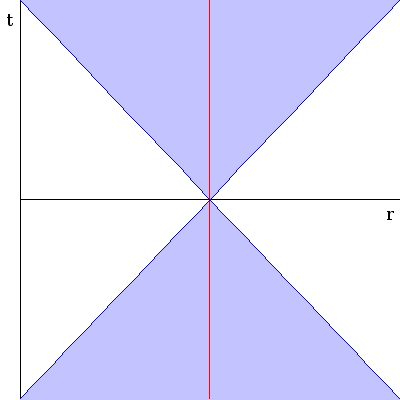
Now the plot thickens: at the instant of time in which both sets of cones were drawn, there was no way for these two objects to communicate. Each was outside the other's light cone, and so no signals could have been sent from one to the other. This implies that there was no way that they could have known that this snapshot was taken at one instant of time: there is in general no such thing as simultaneity between any two observers. In addition, this plot illustrates the notion of horizons: the observer on the right can only be affected by the observer on the left in regions where their light cones overlap, so at the time these light cones were drawn, they were outside each other's particle horizon. We also say that they were separated by a spacelike interval.
In any plot of world lines, if two events are connected by a line shallower than 45 degrees, the interval between them is spacelike. If they are connected by a line steeper than 45 degrees, they are separated by a timelike interval: one's past light cone is within the other's future light cone, and so communication between them along that interval was possible. In the graph above, the upper green region is the region of either world line which can be affected by the event of the other which occurred at t=0 (and whose light cones were drawn in the graph). The lower green region is the region of either world line that could have had an affect on the event of the other which unfolded at t=0.
So if the observer on the right sent a radio message to the observer on the left at the point marked "a", the left-hand
observer would receives that signal at point "b", and the return message would be received by the right-hand observer at point "c".
When velocities are close to that of light, formulas like the Pythagorean Theorem no longer hold and must be modified to take Special Relativity into account. This causes observers moving at relativistic speeds with respect to other observers to measure length and time differently: they will not agree on how long a meter is, or what happens in a minute.
Finally, we feel compelled to remind you that in each of the 2-D world line plots, each point in the r-t plane represents the surface of a sphere, since all directional information has been projected out. Try not to think too hard on that until the rest of this seems natural to you. If you do think about it before you are ready, you will get a headache. Trust us.
©2013, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.