
In the third century BC, the Greek scientist Aristarchus reasoned that the Earth revolves around the Sun. He observed the size of the Earth's shadow on the Moon during an eclipse, and deduced that the Sun was much larger than the Earth and very far away. We can imagine that he reasoned something like this:
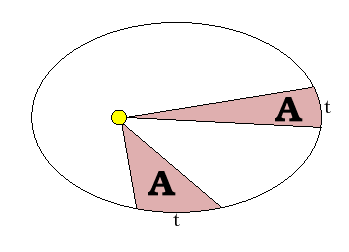
At the beginning of the seventeenth century, Johannes Kepler, working from Tycho Brahe's accurate astronomical observations, provided the first mathematical description of the motions of the planets. Kepler's Laws described both the positions and speeds of the planets as they orbit the Sun:
Galileo Galilei was a contemporary of Kepler's. His invention of the telescope and his careful observations and intricate reasoning contributed greatly to our understanding of the solar system. Galileo was also the first to understand that coordinate systems moving at constant speed relative to one another were equivalent physically. He was excommunicated and imprisoned for publishing the results of this work.
In 1666, Isaac Newton formulated his theory of gravitation, from which Kepler's Laws can be derived. Using the calculus that he developed for this purpose, he found that the force of gravity was proportional to the products of the masses involved (ie., you and the Earth) and inversely proportional to the square of the distance between their centers:
Einstein's theory was developed without the benefit of observational data. He used the mathematical language of geometry and elegantly simple thought experiments about accelerating coordinate systems, and concluded that the presence of mass curves space and freely falling objects follow geodesics (the equivalent of straight lines) in the curved space:
Einstein's theory was subsequently verified by observations, and is the basis of all of the more speculative modern theories involving gravity. Its accuracy is required to explain the details of planetary orbits, to plan space missions and for the implementation of the Global Positioning Satellite system.
This short history of our understanding of the structure of our solar system and the reasons it behaves the way it does provides us with a model for describing the science of physics.
In a somewhat recursive definition, we can say that physics is the study of physical phenomena. As such, its influence is far reaching; in many ways, it provides the fundamental basis for both chemistry and biology. The primary emphasis of this text is the application of physics to problems in those fields. We will see how physics explains the chemical structure of atoms and describes some of the characteristics of chemical reactions. We will also use physics to understand the mechanisms of the human body.
But the bulk of our example was intended to illustrate physics as a science. All science is based on observation: empirical data provides both the motivation for constructing theories and the evidence supporting them. A scientific theory has a domain of application: the theories used to describe subatomic processes are irrelevant when applied to planets. But within its domain of applicability, a scientific theory must not contradict relevant and consistent observational data.
Physics is unique in its use of mathematics as its fundamental language. Different scientists at different times and locations may perform the same experiment with seemingly different results, but if there is a consistent mathematical transformation from one set of results to the other, we find the data in agreement. Similarly, two theories which look very different may in fact be equivalent when a transformation is found which relates their mathematical formulations. Physical theories must be representable using mathematics; it is the basis of their legitimacy.
All science builds upon the work of previous scientists. A scientific theory is not merely a good idea; it is a good idea formulated by a person who is familiar with all of the work done by the scientists before them who thought about the same things. Scientific theories are rarely struck down, due to both the extensive training and immaculate honesty of the scientist. It is much more usual for a theory to be subsumed as a special case of a more general theory, or for a theory to be expanded to a larger domain of applicability.
And as demonstrated time and again in the history of science, a scientist does not allow emotional or political considerations to influence either the data or the theories which explain it. Science in general and physics in particular are concerned with the objective truth: just as an observation must not depend on the identity of the observer, a theory must not depend on beliefs, but upon careful mathematics and rigorous logic.
This is an introductory physics text. It assumes that you have working knowledge of arithmetic, algebra and trigonometry. It also assumes that you are interested in either chemistry or biology, or both. It is an outgrowth of the previous edition: the material is almost identical, but the treatment has been modified based on the way most people seem to learn physics. Interactive programs have been integrated with the text; these programs provide both new material and opportunities to practice problem solving.
We hope that this new edition loses nothing from the previous edition but gains in usefulness for the serious student. More importantly, we hope that you find an interest in physics as you learn about its relevance to your other fields of study.
The next section begins our study of physics with the mechanics of moving objects.
©2003, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
His common sense told him that it is much more likely for a small object to rotate around a larger object than vice versa. Aristarchus was condemned by those who felt they should be at the center of the universe, and eighteen centuries passed before Nicholas Copernicus felt compelled to reexamine his theory.
It is important to note that Kepler came to these conclusions in spite of the fact that his own and the prevailing religious beliefs of the time were in contradiction.
F = G myou mEarth / r2
We will study Newton's theory, which only ceases to be an accurate description of astronomical phenomena in the face of the developments and demands of technology in the last century. As Albert Einstein discovered in 1915, Newton's theory is a special case of the more comprehensive General Theory of Relativity.
Physics as a Science
About this Text
These programs are called applets and are written in the Java programming language. They require a browser with the Java Runtime Environment (JRE). If you cannot see the applets you can
download the JRE.
In addition, the order of topics has been altered in many cases to form a more logical progression, and so that information is not presented until it is needed in a problem solving context. Finally, the material on vectors from the first edition has been included in the appendices.