Notes for Calculus-based Physics

Forces

p ≡ m v,

the force experienced by an object (measured in Newtons: 1 N ≡ 1 kg m/s²) is

F ≡ dp/dt
= dm/dt v + m a
We will refer to this equation as "Newton's laws". In most cases, dm/dt = 0.

Commonly useful forces are:

F = - m g j
This is the force of gravity near the Earth's surface.

Contact forces are those forces experienced by two objects which "push" against each other. When a contact force is exerted between two objects, they both experience the same magnitude of force, but in opposite directions.
F_N is the normal force, perpendicular to the surface on which an object moves (or rests). If an object has a non-zero component of acceleration in the same direction as gravity, the normal force will be the effective weight of the object.

Ropes which do not stretch have a constant tension along their entire length. This tension exerts a force in the direction opposite to every point of connection. We will assume that our ropes (and pulleys) are massless. Objects connected by such a rope (with possible fixed pulleys in between) experience the same magnitude of acceleration. When objects are connected via movable pulleys, the magnitudes of their accelerations are related by integer multiples.

F = μ F_N
This is the force due to friction, acting in the opposite direction of motion. μ is the coefficient of friction (static coefficient of friction if the object is not moving, kinetic coefficient of friction if it is).

F = ρ V g j
This is the buoyant force exerted by a fluid on a sinking object. ρ is the density of the fluid and V is the volume of the object, so the magnitude of the force is equal to the weight of the displaced fluid (Archimedes' principle).

F = - b v
This is the force of drag experienced by an object slowly moving in a fluid; b is the drag coefficient.
If the object has high velocity, the drag force is proportional to the square of the speed.

F = - k Δx
This is the force exerted by a spring. k is the spring constant and Δx is the displacement from equilibrium (where the spring is not stretched). This is known as Hooke's law.
We will assume that our springs are massless. Note that a spring exerts the same magnitude of force on each end, but in opposite directions.

And of course the centripetal force F = m v² / r (pointing toward the center of the circular motion) is responsible for keeping the object in circular motion.

Take an inventory of all the forces acting on each object, in all perpendicular directions (x and y, or parallel and normal if an incline is involved). Gravity is almost always present, and there is a nonzero force in every direction in which there is a nonzero acceleration, so ask yourself what the acceleration is in every direction.

For every direction in which any force acts and the component of acceleration is zero, there must be more than one force acting along that direction!

Then write the vector component equations for Newton's laws for each object or point of connection. Make sure that the relative signs of the forces and the accelerations make physical sense. State specifically the direction of motion associated with positive acceleration for each object under consideration.

Consider the following contraption:

Mass 1 (m₁) is acted upon by the forces of
- gravity (down),
- tension T₁ (up),
- buoyancy (up)
- and drag (up if m₁ is sinking, down if m₁ is rising).

Mass 2 (m₂) is acted upon by
- the force of gravity (down),
- the normal force exerted by the surface (up),
- the contact force between masses 2 and 3 (denoted F₂₃; left if m₂ is moving to the right, 0 otherwise),
- tensions T₁ (left) and
- T₂ (right), and
- the force of friction with the surface (right if m₂ is moving to the left, left if m₂ is moving to the right).

Mass 3 (m₃) is acted upon by
- the force of gravity (down),
- the normal force exerted by the surface (up),
- the contact force between masses 2 and 3 (right if m₂ is moving right, 0 otherwise), and
- the force of friction with the surface (left if m₃ is moving to the right, 0 otherwise).

Mass 4 (m₄) is acted upon by
- the force of gravity (down, producing a component normal to the incline and a component parallel to the incline which contributes to m₄ sliding down the incline),
- tension T₂ (up the incline),
- the force of friction with the surface (down the incline if m₄ is moving up the incline, up the incline if m₄ is moving down the incline), and
- the force due to the spring k (up the incline if the spring is compressed beyond its equilibrium position, down the incline if the spring is stretched beyond its equilibrium position, and 0 if the spring is at its equilibrium position).

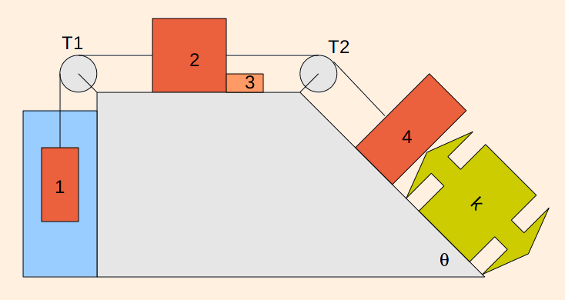
Assuming the motion is to the right, and that all ropes remain taut, Newton's laws are then:

mass	x	y	parallel to the incline	normal to the incline
m₁		T₁ - m₁ g + ρ V g - b v = m₁ a
m₂	T₂ - T₁ - μ N₂ - F₂₃ = m₂ a	N₂ - m₂ g = 0
m₃	F₂₃ - μ N₃ = m₃ a	N₃ - m₃ g = 0
m₄			k (x₀ - x₄) + m₄ g sin θ - μ N₄ - T₂ = m₄ a	N₄ - m₄ g cos θ = 0

Note that x₄ is measured parallel to the incline, and that we have assumed that the spring is extended (x₄ is negative) so that the force due to the spring is pulling m₄ down the incline.

This system of equations is actually a complicated set of differential equations, and is an example of how much easier it is to write down equations in physics than it is to solve them. To make the problem more tractable, we will make the surfaces frictionless (by setting μ to 0), empty the fluid to remove bouyancy and drag (by setting ρ and b to 0), and remove both m₃ and the spring (by setting m₃ and k to 0). The resulting system is a set of three linear equations in three variables (T₁, T₂ and a), with the solution

T₁ = m₁ g (m₂ + m₄ (1 + sin θ)) / (m₁ + m₂ + m₄)

T₂ = m₄ g (m₁ + (m₁ + m₂) sin θ) / (m₁ + m₂ + m₄)

a = (m₄ sin θ - m₁) g / (m₁ + m₂ + m₄)

Note that a > 0 corresponds to motion to the right, so if m₁ > m₄ sin θ, the direction of motion is reversed. And if m₁ = m₄ sin θ, the system is in equilibrium: the net forces are zero.

As long as b and k are zero, this system is still a set of linear equations which we can solve. But if ρ, μ or m₃ are nonzero, we must look carefully at the signs. For μ > 0, the solution is

T₁ = m₁ g (m₂ (1 - μ) + m₄ (1 + sin θ - μ cos θ) ) / (m₁ + m₂ + m₄)

T₂ = m₄ g (m₁ + μ m₂ + (m₁ + m₂) (sin θ - μ cos θ)) / (m₁ + m₂ + m₄)

a = (m₄ sin θ - (m₁ + μ (m₂ + m₄ cos θ)) g / (m₁ + m₂ + m₄)

Now there are values of μ as well as θ which can stop the motion. Note, however, that no value of μ can reverse the motion!

Some forces are the result of measurement in accelerating frames of reference:
- The centrifugal force is the apparent force you experience (in the opposite direction to the centripetal force) because you are in a rotating coordinate system.
- The Coriolis force is the apparent force due to the rotation of the Earth: the tangential speed is a decreasing function of latitude.
- Every local gravitational force is equivalent to measurement in an accelerated reference frame; this is the Einstein equivalence principle.

Be sure to distinguish when gravity is in the same plane as centripetal motion, and when it is perpendicular to the centripetal motion.
- In the former case, ask whether the circular motion acts to make the object seem lighter or heavier.
- In the latter case, there is often an important angle whose tangent is the ratio of the centripetal and gravitational forces.
Consider an object undergoing centripetal motion on a banked track of incline angle θ:
N = m g cos θ - m v² sin θ / r
F_parallel = m v² cos θ / r - m g sin θ - μ N
If the object is not to skid, we must have F_parallel = 0, or
tan θ = (v² - μ g r) / (g r - μ v²).
In the limit θ = 0, the no-slip condition yields
μ = v² / (g r).

(prev) (top) (next)

Please send comments or suggestions to the author.