(prev)(top)(next)

Work and Energy

  1. Work = ∫ F ⋅ dx, measured in Joules (1 J ≡ 1 kg m2/s2).
    Note that if F is perpendicular to dx, no work is done by the force.
    Energy (also measured in Joules) is a quality of matter, not a substance.
    For most practical purposes, the concept of work is used to account for energy losses due to things like friction, or gains in energy due to the application of some external force.

    Efforts to generalize the definition of work lead to massive confusion. Use the integral to determine the magnitude of the work, and then decide if the work increases or decreases the energy of the object.

  2. If the work done on an object is independent of the path the object follows, the force is conservative, and can be expressed as the gradient of a potential energy U:
    F = - (∂U/∂x, ∂U/∂y, ∂U/∂z)
    ≡ - ∇ U
    Note that U is relative since addition of a constant leaves the force unchanged. U = 0 is often chosen to represent a free particle (unaffected by the force), with negative values of U corresponding to a bound particle (confined in space by the force). Also note that this implies that
    U = - ∫ F ⋅ dx.
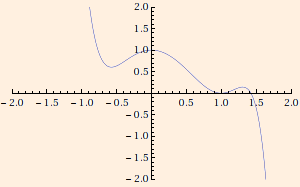
    The direction of the gradient is the direction of the greatest change in U with position.

    The gradient is normal to an equipotential "surface": a surface (or line or point) of constant U:




    U(x) = (x2 - 1)2 - x5 + 2 x6 - x7

    dU/dx = 0 at x = -0.5739, 0, 1 and 1.3059.

    • If the surface is a local minimum of U, the force is zero in all directions, and the system is in stable equilibrium: any small movement leads to a return to the equipotential.

    • If it is a local maximum of U, the system is in unstable equilibrium: the force is zero, but the slightest perturbation away from equilibrium leads to increasing acceleration away from the surface.

    Dissipative forces (such as friction and drag) are not conservative. For conservative forces, the dynamics is completely determined by the potential, so knowing that

    • U = m g y for constant gravitational fields;
    • U = k Δx2 / 2 for springs;
    • U = a r-m- b r-n for interatomic interactions;

    allows you to determine the forces (through the gradient) and therefore the equations of motion.

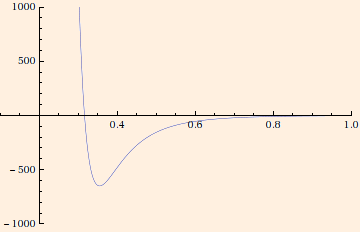
    The last is the a generalization of the Van der Waals Potential, combining a repulsive part and an attractive part to model the interaction energy between two atoms (not in the same molecule). Here r is the distance between their nuclei. It is often used as the "12-6" Lennard-Jones Potential U = a / r12 - b / r6:

  3. The kinetic energy is defined as
    K ≡ m v ⋅ v / 2.

  4. The total energy E ≡ K + U, with
    ΔE = Workexternal.
    Here, Workexternal is understood to include any forces not described by U.

    So in the absence of changes in energy caused by external forces (including dissipative forces), we have conservation of energy:

    ΔE = 0.
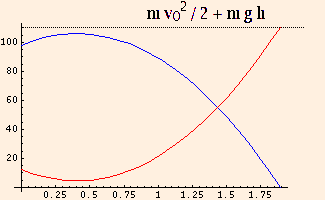
    In this graph, corresponding to an object thrown upward off a cliff, U (blue) = m g y, K (red) = m v2 / 2, and U+K is a constant throughout the object's trajectory:

    In considering the energy of any object moving from an initial state to a final state, identify Ei = Ui + Ki and Ef = Uf + Kf. If Ei > Ef, energy must have been lost because of dissipative work, and

    Ui + Ki - (Uf + Kf) = Wdissipative.
    If Ef > Ei, energy must have been gained by work done on the object by an external force not described by U, and
    Uf + Kf - (Ui + Ki) = Wexternal.
    When conserving energy between steps of a process, energy lost in one step to dissipative forces is not available for the next step.

  5. The rate of change in energy is the power, measured in Watts (1 W ≡ 1 J/s):
    P ≡ dE/dt
    For non-dissipative external work, the integral of the power gives the change in kinetic energy. Assuming m and F are constant:
    ∫ (dW/dt) dt
    = ∫ F ⋅ v dt

    = m ∫ a ⋅ v dt

    = m ∫ dv/dt ⋅ v dt

    = m ∫ v ⋅ dv

    = m v2 / 2

  6. For simple mechanical systems, we can define the Lagrangian as the difference between the kinetic and potential energies:
    L = m v2 / 2 - U(x)
    The principle of least action states that the action
    I ≡ ∫ L dt
    is a minimum for any system which can be described by a Lagrangian. Minimizing the action for our simple mechanical Lagrangian, we have
    dL/dx - d(dL/dv)/dt = 0
    or
    - dU/dx - d(m v)/dt = 0
    which is of course simply Newton's equation. The vast majority of physical systems can be described in this fashion, making the principle of least action perhaps the closest thing we have to a unifying principle in physics.

    Noether's theorem states that a system which has a Lagrangian formulation and a continuous symmetry will have conserved quantities given by (in the case of our simple mechanical Lagrangian)

    dL/dv * v - L
    or
    U(x) + m v2 / 2
    which is of course just the total energy. The continuous symmetry in this case is time translation invariance, which simply means that the Lagrangian does not depend on time.

    The principle of least action and Noether's theorem lie at the foundations of two of the most successful theoretical structures in physics: the Standard Model of Particle Physics and General Relativity.

(prev)(top)(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.