(prev)

(top)

(next)

Angular Motion

1. Uniformly accelerated circular motion is isomorphic to uniformly accelerated linear motion using the substitutions:

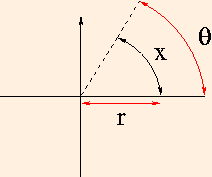
   θ ≡ x / r
   ω ≡ dθ/dt = v / r (angular velocity)
   α ≡ d²θ/dt² = a / r (angular acceleration)

   (Note that r is a constant.) θ is measured as a fraction of a circle in radians (π rad = 180 degrees) and therefore has no physical units. θ = 0 is conventionally taken to be along the positive x axis, with θ increasing with counterclockwise rotation:
   
2. We define the moment of inertia of a rotating object as

   I ≡ ∫ r ⋅ r dm

   where r is the vector perpendicular to the axis of rotation and pointing to the mass dm.

   Moments of inertia are computed the same way as volumes of surfaces of revolution, with the integrands multiplied by the density and the square of the distance to the volume element. You may find the following table of moments of inertia useful:

   cylinder, about symmetry axis	m r2 / 2
   cylinder with a hole, about symmetry axis	m (rinner2 + router2) / 2
   ring, about symmetry axis	m r2
   rod, about center	m l2/ 12
   rod, about end	m l2 / 3
   sphere, about diameter	2 m r2 / 5
   spherical shell, about diameter	2 m r2 / 3

3. Substituting I for mass yields relations for angular momentum L (in place of p), torque τ (in place of F) and rotational kinetic energy:

   L = I ω
   τ = I α
   K_rot = I ω² / 2

   For rolling objects, the angular momentum and energy include contributions both from the rotation of the object about its own center of mass, and from the linear (translational) motion of the center of mass.

   An object that rolls without slipping requires static friction in order roll, but since for every revolution its center of mass moves one circumference, there is no displacement parallel to the frictional force, and so no work is done by friction:

   K_total = K_{translational} + K_rotational.

   Only if an object rolls with slippage, or slides without rolling, does friction cause dissipation of energy.

   The gravitational potential energy of a rotating object is determined by the position of its center of mass.
4. The parallel axis theorem gives the moment of inertia of an object about an axis parallel to an axis through the center of mass:

   I = I_cm + M d²,

   where I_cm is the moment of inertia through the center of mass, M is the mass of the object and d is the perpendicular distance between the parallel axes. Referring to this figure:
   

   we see that

   ∫ r ⋅ r dm = ∫ (d + b) ⋅ (d + b) dm

   = ∫ (d ⋅ d + b ⋅ b + 2 b ⋅ d) dm

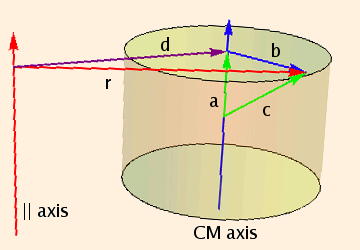
   = M d² + I_cm + 2 d ⋅ ∫ (c - a) dm

   but d ⋅ a = 0 and ∫ c dm = 0 because the origin of c is the center of mass.
5. Using the cross product we can compute angular momentum and torque vectors in terms of linear quantities:

   L = r ⊗ p

   τ = r ⊗ F

   (with axes of rotation passing through the origin of r). r is called the lever arm.

   Note that point objects moving linearly can have angular momentum. For instance, an object of mass m moving at speed v along the line y = b has angular momentum with respect to the origin

   L = (v * t, b, 0) ⊗ m (v, 0, 0)

   = (0, 0, - b m v)

   Note that the units of torque are Newton-meters, not Joules. Work results from a force exerted parallel to the direction of motion; torque results from a force exerted perpendicular to both the lever arm and the axis of rotation.
6. In the absence of external torques, the angular momentum of a system of objects is conserved:

   ΔL = ∫ τ_external dt

   Note that:
   • L_i, L_f and τ_external must be computed with respect to the same fixed axis.
   • Any object included in the calculation of L_i must be included in the calculations of L_f and τ_external.
   • You can choose any vector to serve as the axis, but some choices are far wiser than others. If a force acts at the axis, its lever arm is zero and therefore it exerts no torque about that axis.
   • Unless an object moves in a plane perpendicular to the plane of rotation, it has angular momentum with respect to the axis of rotation.

(prev)

(top)

(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.