
| (prev) | (top) | (next) |
Note that the electric field has units both of N / C and V / m. Think of it both as a force per unit charge and a potential per unit distance.
The direction of the electric field at a point is defined as the direction of the acceleration experienced by a positive test charge:
Since the electric field is minus the gradient of the potential field,
Consider again the line of charge extending from -b to b. We could compute the electric field using
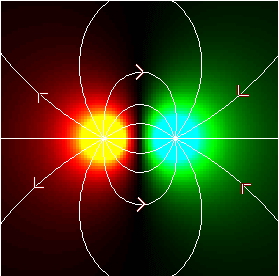
The Electric Field
F = - ∇ U = - qt ∇ V.
We define the (vector) electric field
(Coulomb's law):
E(x,y,z) ≡ - ∇ V(x,y,z)
The vector r in the integrand is the vector pointing from the charge dq to the field point.
The integrand is most often written as q times the unit vector pointing in the r direction, divided by r2, but this expression is more useful
unless the problem is 1-dimensional.
Either way, the field (and therefore the force) decreases as 1/r2.
= (1 / (4 π ε)) ∫ r dq / r3
ΔV = - ∫ E ⋅ ds,
where the integral is along a path between two field points.
E(x,y) = (λ / (4 π ε)) ∫-bb (x - s, y) ds /
(√ ((x - s)2 + y2))3
or we can use
E(x,y) = - ∇ V(x,y)
If the field point is on the y axis, this becomes
= (λ / (4 π ε)) (1 / √((b - x)2 + y2) - 1 / √((b + x)2 + y2),
((b - x) / y) / √((b - x)2 + y2) + ((b + x) / y) / √((b + x)2 + y2))
E(y) = λ b / (2 π ε y √ (b2 + y2)) j
In the limit b → ∞, this is
E(x,y) = λ / (2 π ε y) j
| (prev) | (top) | (next) |
©2010, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.