(prev)

(top)

(next)

Gauss' Law

1. Define the electric flux through a surface

   Φ ≡ ∫ E ⋅ dA

   where the direction of dA is the outward unit normal to the surface.
2. Gauss' law (which is an application of Stoke's theorem: ∫_M dw = ∫_∂M w) then states that

   Φ_{closed surface} = q_inside / ε

   Gauss' law is especially useful when the electric field is constant along faces of the closed surface, and is either perpendicular to or parallel to each of the faces. The following "Gaussian surfaces" are often useful:
   • for spherically symmetric charge distributions, use a concentric sphere; E will be normal to the surface:
     A solid charged ball of radius a, field point a distance r from the center:

     

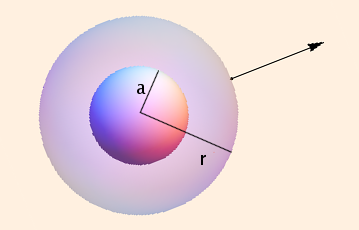
     E * 4 π r² = 4/3 π a³ ρ / ε

     E = a³ ρ / (3 ε r²)

   • for axially symmetric charge distributions, use a coaxial cylinder; E will be normal to the axis if the cylinder is sufficiently far from the ends of the distribution:
     A line of charge with field point at distance r, Gaussian cylinder of height h:

     

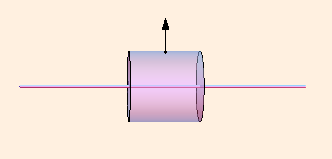
     E * 2 π r h + 0 * 2 * π r² = h λ / ε

     E = λ / (2 π ε r)

   • for a plane-symmetric charge distribution, use a cylinder whose axis is normal to the surface and intersects it; E will be normal to the end caps if the cylinder is sufficiently far from the edges of the distribution:

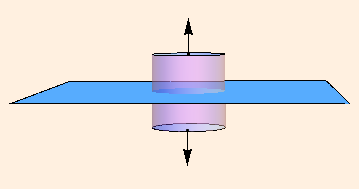
     Plane at z = 0, field point at (0,0,z), Gaussian cylinder of radius r and height 2z:

     

     E * π r² + E * π r² + 0 * 2 π r * 2 z = π r² σ / ε

     E = σ / (2 ε)

   Remember that the Gaussian surface must intersect the field point!
3. What is "sufficiently far from the edges of the distribution"?

   Consider again the electric field due to a linear charge density λ extending from (-b,0) to (b,0), with the field point at (0,y). Ignoring the finite length, Gauss' law gives us

   E_Gauss = λ / (2 π ε y)

   Coulomb's law gives

   E_y = λ b / (2 π ε y √ (y² + b²))

   The ratio of the two is

   E_y / E_Gauss = 1 / √ (1 + (y / b)²)

   ≈ 1 - 1 / (2 (b / y)²)

   (using a Taylor series in x = y / b) in the limit b >> y.

   So, for instance, if the ends are 10 times further away than the field point, the error is 0.5 %.

   For a disc of radius b, thickness d and charge density ρ (with the field point again a distance y from the center and ignoring the finite radius for Gauss' law),

   E_Gauss = ρ d / (2 ε)

   E_z = ρ (d + √ ((y + d)² + b²) - √ (y² + b²)) / (2 ε)

   E_z / E_Gauss = 1 - (b / d) (√ (1 + (y / b)²) - √ (1 + ((y + d) / b)²))

   ≈ 1 + 1 / (b / y) + 1 / (2 b / d)

   in the limits b >> y and b >> d. So if the edge is 10 times further away than the field point, the error is now 10 % for negligible thickness, but climbs to 15 % if the radius is only 10 times the thickness.

   For less symmetric shapes (like rectangles), the closest edge is most important in determining the error.

   Note that any finite charge distribution looks like a spherically symmetric charge distribution from sufficiently far away.

4. Consider a conducting sphere of radius r₁ and charge q₁. We know that all of the charge resides on the surface.

   It is surrounded by a spherically symmetric nonconducting shell, extending to a distance r₂ from the center of the sphere, with uniform charge q₂.

   That in turn is surrounded by a neutral conducting shell which extends to a distance r₃ from the center of the sphere:

   

   In order for Gauss' law to hold, this latter shell must have charge -(q₁ + q₂) on the inside surface and charge q₁ + q₂ on the outside surface, since E = 0 inside.

   We can use Gauss' law to compute the magnitude of the electric field everywhere in space:

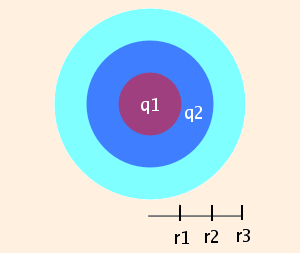
   r ≤ r1	E = 0
   r1 < r < r2	E = (1 / (4 π ε)) (q1 / r2 + q2 ((r3 - r13) / (r23 - r13)) / r2)
   r2 ≤ r ≤ r3	E = 0
   r > r3	E = (1 / (4 π ε0)) (q1 + q2) / r2

(prev)

(top)

(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.