(prev)

(top)

(next)

Electromagnetic Waves

1. Maxwell's correction to Ampere's law for time varying electric fields is:

   ∫_{closed loop} B ⋅ ds = μ (I + ε dΦ_E/dt).

2. Taking this with Faraday's law, we see that time-varying electric fields produce magnetics fields and vice versa.

   Given that such electromagnetic fields propagate energy in the direction of E ⊗ B, we examine an instant when E is along the y axis. For propagation along the x axis, B will be along the z axis. Applying Faraday's law to a loop of height dy and width dx normal to B:

   

   we have

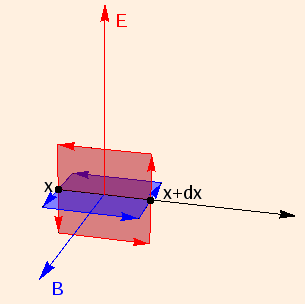
   E(x + dx) * dy - E(x) * dy = - d(dx * dy * B)/dt

   which in the limit dx → 0 becomes

   dE/dx = - dB/dt.

   Applying Ampere's law (with I = 0) to a loop of height dz and width dx normal to E gives us

   B(x) * dz - B(x + dx) * dz = μ ε d(dx * dz * E)/dt

   which in the same limit becomes

   dB/dx = - μ ε dE/dt.

   Differentiating the first equation with respect to x and the second with respect to t and equating the results gives us the electromagnetic wave equation for E:

   d²E/dx² = d²E/dt² / c²

   with propagation velocity

   c = 1 / √(μ ε) = 2.998 * 10⁸ m/s = the speed of light.

   Doing the reverse gives us the (same) wave equation for B.
3. Substituting E(x,t) = E cos (k x - ω t) and B(x,t) = B cos (k x - ω t) into dE/dx = - dB/dt, we find that the amplitudes are related by

   E / B = ω / k = c.

4. The various types of electromagnetic radiation differ only by their wavelength:

   radiation	λ	ν (Hz)	energy (eV)	source
   radio	> 1 m	< 3 * 108	< 1.24 * 10-6	low-energy atomic or molecular motions
   microwave	> .1 mm	< 3 * 1012	< .0124	rigid molecular motions
   infrared	> 7000 Angstroms	< 4.3 * 1014	< 1.78	molecular bond motions
   visible light	> 4000 Angstroms	< 7.5 * 1014	< 3.1	atomic electron transitions
   ultraviolet	> 50 Angstroms	< 6 * 1016	< 248	atomic electron transitions
   x-rays	> .03 Angstroms	< 1020	< 414 K	electron transitions in heavy atoms
   gamma rays	< .03 Angstroms	> 1020	> 414 K	nuclear decays

   Electromagnetic waves also undergo Doppler shifting, as shown here:

   
5. The Poynting vector is

   S = E ⊗ B / μ,

   with units of W / m². Since the integral of cos² over one wavelength is 1/2, the intensity is

   <S> = E² / (2 μ c)

   = c <u>

   with u equal to the sum of the electric and magnetic energy densities:

   ε E² / 2 + B² / (2 μ) = E² / (2 μ c²) + (E / c)² / (2 μ)

   = E² / (μ c²)

   ("<>" denotes the average over one wavelength, which introduces the factor of 1/2).

   This implies that the electromagnetic field exerts a pressure

   P = S / c

   (under conditions of perfect absorption). Pressure is measured in Pascals: 1 Pa ≡ 1 N / m².

   Note that the units of pressure are identical to those of energy density.

6. The electromagnetic momentum density p = S / c². Conservation of momentum implies that under conditions of perfect reflection, the pressure

   P = 2 S / c.

(prev)

(top)

(next)

©2012, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.