1. In optics,
   • I is the image distance, O is the object distance, f is the focal length and R is the radius of curvature of a spherical lens or mirror.
   • R is positive for lenses (and negative for mirrors) if the center of curvature is on the opposite side of the light from the object.
   • For a flat surface, R = ∞.
   • The magnification M = - I / O, which also equals - image size / object size. If M < 0, the image is inverted.

   I and f are positive for lenses (and negative for mirrors) if they are on the opposite side of the lens or mirror from the light from the object:

   

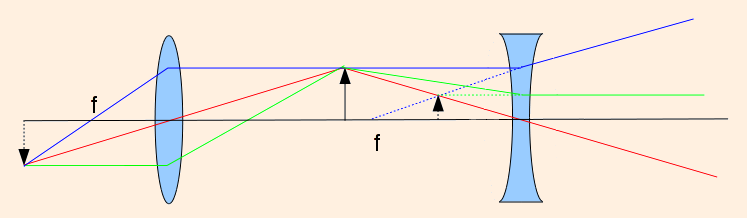
   converging lens	diverging lens
   I > 0	I < 0
   Renter > 0	Renter < 0
   Rexit < 0	Rexit > 0
   f > 0	f < 0
   M < 0	M > 0
   real image	virtual image

2. 1 / I + 1 / O = 1 / f.

   This is called the thin lens equation.

   Combining it with the definition of magnification, we find that

   M = f / (f - O)

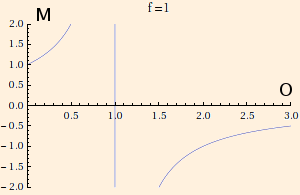   This means that for negative f (diverging lenses and convex mirrors), 0 < M < 1.

   It also means that for positive f (converging lenses and concave mirrors),

   • if O < f, M > 1;
   • as O → f ^-, M → ∞;
   • for O > f, M < 0;
   • as O → f ⁺, M → -∞;
   • when O = 2 f, M = -1; and
   • as O → ∞, M → 0.
   
   
3. 1 / f = 2 / R for a mirror.
4. 1 / f = (n - 1) (1 / R_enter - 1 / R_exit) for a lens in air.

   This is called the lens maker's equation.

   If f in measured in meters, s = 1/f is the lens strength measured in diopters.

   For compound lenses, the strengths are additive.

5. For light refracting from medium 1 to medium 2 through a spherical surface of radius R,

   n₂ / I + n₁ / O = (n₂ - n₁) / R.

(prev)

(top)

(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.