(prev)

(top)

(next)

Quantum Principles

1. Electromagnetic radiation travels in waves, but it interacts with matter in discrete energy transfers via photons. The energy of a photon is proportional to its frequency:

   E = h ν,

   where h is Planck's constant = 6.626 * 10^-34 J s.
2. This quantized transfer of energy explains the spectrum of radiation emitted by a black body: an object which absorbs all radiation incident on it. The radiation increases the thermal motion of the atoms and molecules in the body, which then re-radiates energy in a thermal spectrum. The resulting Planck (black body) distribution of intensity per unit wavelength, as a function of wavelength and temperature (K), is

   I(λ,T) = 2 π h c² / (λ⁵ (e^{h c / (λ k_B T)} - 1))

   where k_B is Boltzmann's constant = 1.381 * 10^-23 J / K:
   

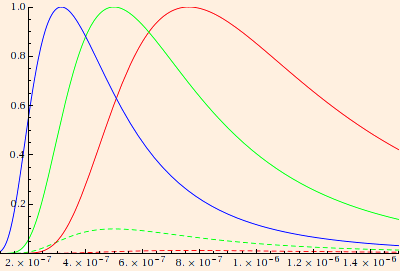
   (The solid normalized curves correspond to the surface temperatures of Sirius A (9200 K), Sol (5800 K) and Betelgeuse (3800 K). The dashed curves are proportional intensities for Sol and Betelgeuse.)

   For a given temperature, the maximum is located at (2.9 * 10^-3 m K) / T (Wien's law).
3. In the photoelectric effect, light incident on a material can free electrons from the material via the momentum transfer from photons:

   p = h / λ.

   If φ energy is required to eject an electron, a potential ΔV_s can be applied which will stop the process:

   e ΔV_s = h ν - φ

   where ΔV_s is the stopping potential and φ is the work function. The frequency corresponding to zero stopping potential is ν_cutoff: the minimum frequency required to eject an electron. Note that this relationship is independent of intensity.
4. The Heisenberg uncertainty principle states that

   Δx Δp_x ≥ h / (4 π)

   and

   ΔE Δt ≥ h / (4 π)

   Think in terms of the wavelength required to resolve a particle, and the resulting recoil.
5. We now know four fundamental constants of nature:
   • the speed of light, c = 299792458 m/s, which is the greatest possible speed;
   • the electrical permittivity of the vacuum, ε₀ = 8.85418782 * 10^-12 C²/(N m²), which determines the strength of the electrical field;
   • Newton's gravitational constant, G = 6.67428 * 10^-11 N m² / kg², which determines the strength of the gravitational field; and
   • Planck's constant, h = 6.62606896 * 10^-34 J s; the smallest possible angular momentum is h / 2.

   These constants can be combined to set natural scales for our fundamental units:

   • the Planck length, L_P = √ (h G / c³) = 4.05134 * 10^-35 m;
   • the Planck time, t_P = √ (h G / c⁵) = 1.35138 * 10^-43 s;
   • the Planck mass, m_P = √ (h c / G) = 5.45552 * 10^-8 kg; and
   • the Planck charge, q_P = √ (ε₀ h c) = 1.32621 * 10^-18 C.

   (Some sources define these quantities in terms of h / (2 π) instead of h, or 4 π ε₀ instead of ε₀, but the orders of magnitude are essentially unchanged.)

   L_P and t_P are often interpreted as the smallest measurable intervals of distance and time; m_P is the mass of 5.9989 * 10²² electrons, and q_P is the charge on 8.27756 electrons (as defined here).

   It is also interesting to note that these constants can be combined in easy ways so as to "convert" one fundamental unit into any other; in General Relativity (a geometric theory), it is usually convenient to express everything in terms of length, so that

   • mass * G / c² → length;
   • time * c → length;
   • angular momentum / unit mass / c → length; and
   • charge * √ (G / ε₀) / c² → length.

   This suggests that if indeed there is a theory which encompasses all physical phenomena (at least at the smallest scales), that all of the fundamental physics quantities (length, time, mass and charge) will be interrelated.

(prev)

(top)

(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.