(prev)(top)(next)

The Atom

  1. The Bohr quantization condition specifies that only a discrete set of values are allowed for the "orbital" angular momentum of an atomic electron:
    m v r = n h / (2 π).
    Equating the     centripetal force to the Coulomb force (and E = K + U) gives us a corresponding discrete spectrum of orbital radii and energy levels:

    where Z is the nuclear charge, the Bohr radius

    a0 = ε h2 / (π m e2)
    = .529 * 10-10 m (= .529 Angstroms)
    and the Rydberg energy
    E0 = m e4 / (8 ε2 h2)
    = 13.606 electron Volts (1 eV = e J)
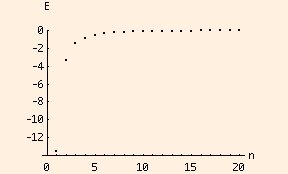
    These are the first 20 energy levels of a Hydrogen atom:

  2. In quantum mechanics, the momentum operator is
    P ψ = - i (h / (2 π)) dψ/dx,
    and the energy operator is
    E ψ = i (h / (2 π)) dψ/dt,
    where ψ(x, t) is the electron wave function. With these prescriptions, the statement of conservation of energy becomes Schrodinger's equation:
    E ψ = P2 ψ / (2 m) + U(x) ψ
    or
    i (h / (2 π)) dψ/dt = - (h / (2 π))2 / (2 m) ∇2 ψ + U(x) ψ
    Here ∇2 ψ ≡ ∇ ⋅ (∇ ψ). In general, solving this differential equation is beyond our present means. But if we restrict ourselves to spherically symmetric wave functions, where now
    ∇2 ψ = d(r2 dψ/dr)/dr / r2,
    and take ψ(x, t) = ψ(r) χ(t), with the Coulomb potential energy Schrodinger's equation becomes
    i (h / (2 π)) dχ(t)/dt / χ(t) = - ((h / (2 π))2 (2 dψ/dr + r d2ψ/dr2) / (2 m r) + (- e2 / (4 π ε r)) ψ) / ψ
    This equation is obviously separable, and so both sides equal a constant (E). The solution for χ is
    χ(t) = e-i E t / (h / (2 π))
    and the right hand side is equivalent to the Laguerre equation. In general, it too is beyond our capabilities, but the first few solutions are instructive:

    1. ψ1(r) = (1 / √ (π a03)) e- r / a0, E = - E0, <r> = 3 a0 / 2

    2. ψ2(r) = (1 / √ (32 π a03)) 2 (1 - r / (2 a0)) e- r / (2 a0), E = - E0 / 4, <r> = 6 a0

    3. ψ3(r) = (1 / √ (243 π a03)) (3 - 6 r / (3 a0) + 2 (r / (3 a0))2) e- r / (3 a0), E = - E0 / 9, <r> = 27 a0 / 2

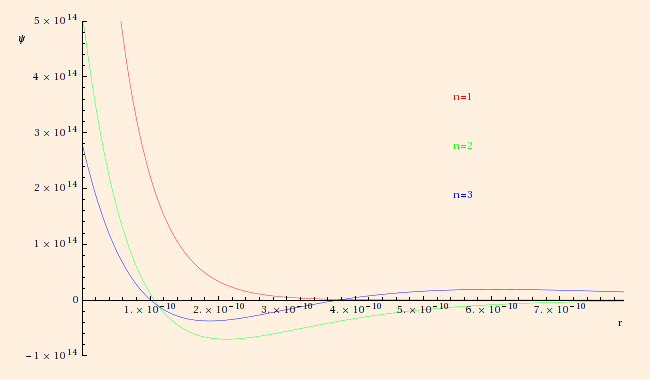
    These wave functions have been normalized such that ∫all space ψ2 dx3 = 1.

    <r> is the expected value (the most "probable value"), and is computed using

    <r> = ∫ ψ2 r dx3,
    which in our case is
    4 π ∫0∞ ψ2 r3 dr.
    If we interpret <r> as the most probable value, ψ takes the role of a probability amplitude, and ψ2 (which in general is ψ* ψ, since ψ can be complex) takes the role of a probability distribution.
    Note the agreement with our previous analysis based on Bohr's quantization condition. While the expectation values for r are not the same, if we substitute 3 a0 / 2 for a0 in Bohr's results, they still obey the relation
    rn = n2 a0 / Z
    Note too that the second and third solutions have nodes at r = 2 a0 and r = 3 (3 +- √ 3) a0 / 2, respectively. These nodes are reminiscent of the nodes in standing waves, and lead to a similar interpretation for the electron wave functions.

    Also note that as decaying exponentials, they only approach zero asymptotically, but they have significant nonzero portions far beyond the orbital radii suggested by Bohr's model.

    Finally, note that for a hydride ion (H-), the electron wave functions overlap.

  3. The energy level "n" is not the only quantum number; the angular portion of Schrodinger's equation can also be separated, and the resulting solutions are labeled by this complete set of quantum numbers:

    This applet will draw three dimensional plots of several complete (not simply spherically symmetric) electron wave functions for Hydrogen atoms and Hydride ions.
    These quantum numbers explain the form of the periodic table.

    Because of charge screening of the nuclear charge by intervening electrons, electrons in an energy level n>1 of multielectron atoms see an effective nuclear charge of approximately n.

(prev)(top)(next)

©2012, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.