(prev)(top)(next)

Temperature and Heat

  1. The temperature in Kelvin is 273.15 + the temperature in Celsius. Henceforth we will assume that all temperatures will be in Kelvin.
    Note that since Celsius and Kelvin temperatures differ by an additive constant, a difference in temperatures ΔT is numerically the same in either unit.

  2. Avogadro's number NA = 6.022 * 1023, is the number of atoms or molecules in a mole. We will assume that we are working with numbers of atoms or molecules on the order of NA.

  3. The heat required to change the temperature of an object is
    Q = m c ΔT = C ΔT,
    where c is the specific heat of the substance and C is the heat capacity of the object.

    When the volume is constant, we often write

    ΔQ = n cv ΔT
    where n is the number of moles and cv is the molar specific heat at constant volume.

    Likewise, when the pressure is constant, we often write

    ΔQ = n cp ΔT,
    where cp is the molar specific heat at constant pressure.

  4. The heat required to change the phase of a substance is
    Q = m L,
    where L is the latent heat (Lf of fusion or Lv of vaporization).

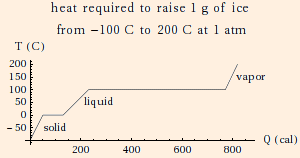
    c(water) = 1 cal/gK (1 cal (calorie) = 4.186 J)Lf(water) = 80 cal/g
    c(ice) = 0.51 cal/gKLv(water) = 540 cal/g
    c(water vapor) = 0.48 cal/gK (at constant pressure)

  5. The thermal power of conduction is
    dQ/dt = k A dT/dx,
    where k is the thermal conductivity, A is the cross-sectional area through which heat is being transferred and dT/dx is the temperature gradient. This expression is isomorphic to Ohm's law with the substitutions:

  6. The thermal power of radiation is
    dQ/dt = σ A e T4,
    where σ is the Stefan-Boltzmann constant (5.67 * 10-8 W / (m2 K4)) and e is the emissivity, equal to the fraction of incoming radiation which is absorbed. An emissivity of 1 corresponds to a black body.
    This result follows from integrating the black body distribution from λ = 0 to ∞. That integral is the power per unit area, and e < 1 if the source is not a black body. The Stefan-Boltzmann constant is the coefficient of T4 in the integral, equal to
    2 kB4 π5 / (15 c2 h3).

  7. The coefficient of linear expansion α is defined via a Taylor series expansion of the length as a function of temperature, analogously to the temperature coefficient of resistivity.

  8. For ΔT << 1, the volume coefficient of expansion is β = 3 α (use the binomial expansion).

(prev)(top)(next)

©2012, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.