Notes for Calculus-based Physics

Statistical Mechanics

Assuming a uniform gas, the Boltzmann distribution gives the fraction of particles which have energy E:

f(E) ~ e^{-E / (k T)}.
Note: this assumes that the particles in the gas are distinguishable. If they are not, the distribution function depends on the spin of the particles. For particles of integer spin, we have the Bose-Einstein distribution
f(E) ~ 1 / (A e^{E / (k T)} - 1),
and for particles of half-integer spin, we have the Fermi-Dirac distribution
f(E) ~ 1 / (A e^{E / (k T)} + 1).

If all of the energy is kinetic, and the gas is uniform, f(E) = e^{-m v² / (2 k T)} = f(v).

Note that this is a normal distribution with standard deviation √ (k T / m). For air at room temperature (with molecular weight 28.94 g, temperature 20 C and mean speed 463 m/s), σ = 290.244 m/s:

In three dimensions we normalize this with respect to position and velocity as

∫ f(v) d³r d³v = N,

where N is the total number of particles in the gas. Now d³r = dV; assuming that the velocity distribution is isotropic (does not depend on direction, i.e., is spherically symmetric), we have

d³v = 4 π v² dv.

Integrating with respect to v from 0 to ∞, we find

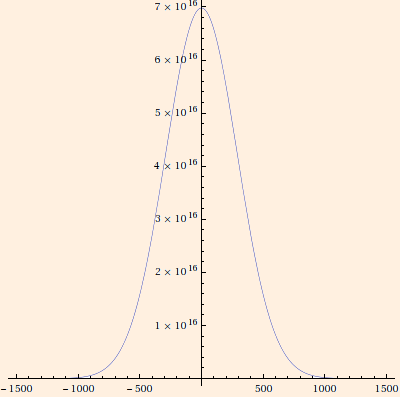
f(v) = (N / V) (m / (2 π k T))^3/2 e^{-m v² / (2 k T)}.
(Here we used ∫₀^∞ x² e^{-a x²} dx = (√ π) / (4 a^3/2).)

The graph above was plotted using this normalization and standard pressure, for a mole of air occupying 22.4L. The right side of the plot is the relevant part, considering we are now treating v as a speed. For the 3-dimensional isotropic normal distribution, almost 87% of the molecules will have speeds within one standard deviation of the mean.

The average of a function g(v) weighted by a distribution f(v) is

<g(v)> = (V / N) ∫ g(v) f(v) d³v.

The pressure due to collisions of gas particles (taking z normal to the wall) is:

P = F_z / A = dp_z/dt / A
= (1 / A) * the number of particles colliding per unit time * average momentum transfer
<P> = (1 / A) ∫ f(v) * (A dz / 2) / dt * 2 m v_z d³v

(V = A dz, and half of the particles are moving away from the wall during the time dt)
= m ∫ f(v) v_z² d³v
= m N <v²> / (3 V)
(<v_z²> = <v²>/3 since v is isotropic)
= 2 N <E> / (3 V)

An ideal gas is a dilute gas whose constituents can be assumed to be non-interacting (except for perfect collisions). The equation of state for an ideal gas is
P V = n R T,
where P is the pressure, V is the volume, n is the number of moles, and T is the temperature.
R = N_A k_B is the molar gas constant, equal to 8.314 J / (mol K).
Equations of state are usually thought of as relating pressure and density; in those terms, the ideal gas equation of state is
P = (R T / (molecular weight)) ρ.

So for an ideal gas, we find <E> = 3 P V / (2 N) = 3 n R T / (2 N) = 3 k T / 2.
In general, the Equipartition theorem tells us that each quadratic degree of freedom in <E> contributes k T / 2.

The first law of thermodynamics is a statement of conservation of energy:
dE = dQ + dW
where dE is the change in energy of the system, dQ is the heat added to it and dW is the work done on it:
W = -∫ P dV

For an ideal gas with χ*N quadratic degrees of freedom,
c_v = dQ/dT / n = dE/dT / n

(constant volume implies that W = 0)
= d(χ N k T / 2)/dT / n
= χ R / 2

and
c_p = dQ/dT / n = (dE/dT + P dV/dT) / n
= c_v + R.
(since P is constant, P dV/dT = d(P V)/dT = n R )

χ is the sum of translational, rotational and vibrational modes. All atoms and molecules possess 3 translational degrees of freedom; linear molecules have 2 more rotational modes, whereas nonlinear molecules have 3 more rotational modes. Vibrational degrees of freedom require sufficient energy to rise to an excited quantum state. For gases, room temperature is mostly insufficient to the task. Note that vibrational modes have both a kinetic and a potential degree of freedom.

Define γ ≡ c_p / c_v. For an ideal gas undergoing an adiabatic process (in which ΔQ = 0),
dE = n c_v dT = - P dV.
Since
d (P V) = P dV + dP V = n R dT
= - (R / c_v) P dV
= - (γ - 1) P dV

we have
dP V = - γ P dV.
Integrating we find
P V^γ = constant.
Note that for an ideal gas, γ = 1 + R / c_v = 1 + 2 / χ.

Note that the ideal gas is not the only equation of state!
- The Van der Waals equation of state describes a gas of molecules that have both finite size and weak interactions:
  (P + α β / ν²) (ν - β) = R T,
  where α is the interaction energy in Joules per mole, ν is the molar volume of the gas, and β is N_A times the effective volume of a single molecule (which is approximately 4 times the actual volume, since the center of another molecule cannot be closer than 2 molecular radii away). Notice that in the limit of non-interacting point-like molecules, the Van der Waals equation of state reduces to that of an ideal gas.
- In polytropic processes,
  dQ/dT = n * a constant (c)
  The polytropic index
  κ = (c_v - c) / (c_p - c_v)
  has useful values
  - 0 describing a star of constant density;
  - 0.5 to 1 describing a neutron star;
  - 1 describing a star whose radius is independent of the central density;
  - 1.5 to 3, approximating a white dwarf, which is supported by electron degeneracy pressure;
  - 3 describing a star whose mass is independent of the central density, which is supported equally by radiation pressure and ideal gas pressure (ie., the Sun);
  - 5 describing a star of infinite radius (ie., a nascent stellar system);
  - ∞ describing an isothermal gas sphere (like a globular cluster).
  The polytropic equation of state is
  P ~ ρ^{1 + 1/κ}.
- Another equation of state is useful in cosmology, where
  P = w ρ
  and
  - w = 0 describes pressureless dust;
  - w = 1/3 describes radiation;
  - w = -1 describes the cosmological constant, which seems to account for the acceleration of the expanding universe.

(prev) (top) (next)

Please send comments or suggestions to the author.