(prev)

(top)

(next)

Thermodynamics

1. Thermodynamic processes can be:
   • isothermal processes, ΔT = 0 (so P ~ 1 / V);
   • isobaric processes, ΔP = 0 (so T ~ V);
   • isovolumetric or isochoric processes, ΔV = 0 (so T ~ P);
   • adiabatic processes, ΔQ = 0 (so P ~ 1 / V^γ);
   • cyclic processes, all state variables (P, V, T, E, S) return to their original values after each cycle.

   (Throughout, we will assume the processes involve an ideal gas with constant n.)

   In a cyclic process, the state variables all return to their initial values after one cycle.

2. Thermodynamical systems are often described using PV diagrams, with pressure plotted on the vertical axis and volume plotted on the horizontal axis. In such a diagram, the area under a curve is easily related to work:
   

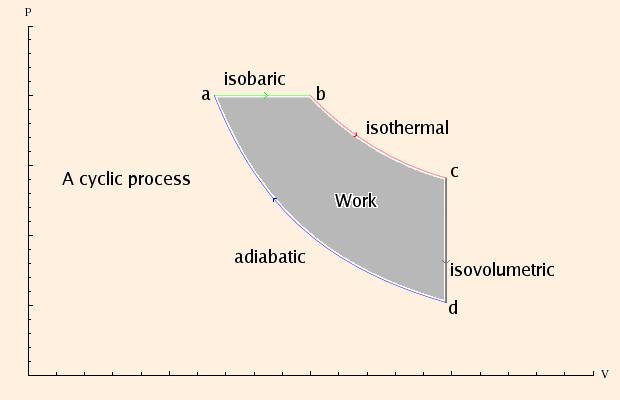
   Assuming this PV diagram describes a process involving an ideal gas, we can deduce the following:

   as a→b	Pa = Pb	ΔEa→b = n cv (Tb - Ta)	ΔQa→b = n cp (Tb - Ta)	Wa→b = -Pa (Vb - Va)
   at b	Tb = Pb Vb / (n R)	Tb > Ta	ΔQa→b > 0	Wa→b < 0
   as b→c	Tb = Tc	ΔEb→c = 0	ΔQb→c = -Wb→c	Wb→c = -n R Tb ln (Vc / Vb)
   at c	Tc = Pc Vc / (n R)		ΔQb→c > 0	Wb→c < 0
   as c→d	Vc = Vd	ΔEc→d = n cv (Td - Tc)	ΔQc→d = n cv (Td - Tc)	Wc→d = 0
   at d	Td = Pd Vd / (n R)	Td < Tc	ΔQc→d < 0
   as d→a	Pd Vdcp/cv = Pa Vacp/cv	ΔEd→a = n cv (Ta - Td)	ΔQd→a = 0	Wd→a = n cv (Ta - Td)
   at a	Ta = Pa Va / (n R)	Ta > Td		Wd→a > 0

   In addition, we know that ΔE_a→b + ΔE_c→d + ΔE_d→a = 0, but in this case it only tells us that T_b = T_c.

   From this we can compute the total heat added during the cycle:

   n c_p (T_b - T_a) + n R T_b ln (V_c / V_b)

   and the total work done by the gas:

   P_a (V_b - V_a) + n R T_b ln (V_c / V_b) - n c_v (T_a - T_d),

   corresponding to the shaded area in the PV diagram.

   Note that heat enters this "engine" in steps a→b and b→c, and exits it in step c→d; the total work done by the engine is positive. If the cycle were operated in reverse, it would be a "refrigerator", taking heat from a cooler environment during step d→c and exhausting it to a warmer environment from c→a; the total work done by the refrigerator is negative. The meaning of this is that it requires external work to move heat from a cooler to a warmer place.

3. To see how this information is applied to a problem, consider the following thermodynamic cycle for n = 4 moles of a monatomic ideal gas:
   
   1. from a to b, the system undergoes an isovolumetric increase in pressure;
   2. from b to c, the system undergoes an isothermal expansion;
   3. from c to d, the system undergoes an isobaric compression;
   4. from d to a, the system undergoes an adiabatic compression.

   Suppose we are given P_a = 200,000 Pa, P_b = 300,000 Pa, P_c = 100,000 Pa and V_a = 65 L.

   We know that P_d = P_c, V_b = V_a, and T_b = T_c. We can use the ideal gas law to compute the temperatures at points a and b from the pressure and volumes at those points: 390.907 K and 586.36 K, respectively. From the latter we can compute the volume at point c, which is 195 L.

   We can use the adiabatic equation for an ideal gas:

   P_d V_d^γ = P_a V_a^γ,

   to compute V_d = 98.5216 L. Finally, we can use the ideal gas law to find that T_d = 296.252 K.

   Since b to c is an isothermal expansion, the first law tells us that ΔQ_b→c = - ΔW_b→c. Using the ideal gas law, we find

   ΔW_b→c = - ∫_b^c P dV

   = - n R T_b ∫_b^c dV / V

   = - n R T_b ln (V_c / V_b) = -21,422.9 J.

   (Note the sign: the gas does external work.)

   Using the equations for isovolumetric and isobaric processes, we have

   ΔQa→b = n cv (Tb - Ta)	ΔQb→c = n R Tb ln (Vc / Vb)	ΔQc→d = n cp (Td - Tc)	ΔQd→a = 0
   = 9750 J	= 21,422.9 J	=-24,119.6 J

   Finally, consistent with the fact that ΔE = 0 for a cycle, we compute

   ΔWa→b = 0	ΔWb→c = - n R Tb ln (Vc / Vb)	ΔWc→d = Pc (Vc - Vd)	ΔWd→a = cv (Pa Va - Pd Vd) / R
   	= -21,422.9 J	= 9647.84 J	= 4721.76 J

4. The efficiency of an engine is

   ε = W / Q_h

   = (Q_h - Q_c) / Q_h

   = 1 - Q_c / Q_h.

   Here, energy is taken in as Q_h, work W is done by the engine, and the waste heat is discharged as Q_c.

   In the example above, Q_h = 31,172.9 J, W = 7053.33 J, Q_c = 24,119.6 J and ε = 22.6265%.

   This calculation obscures some interesting facts:

   • for this cycle, as the number of degrees of freedom of the gas χ→∞ (with all other values unchanged), ε→0 as 1/χ (more heat must be removed during isobaric cooling to lower the temperature the same amount, because more of the heat comes from non-translational degrees of freedom which do not affect temperature);
   • ε does not depend on n; increasing n will only lower the temperatures (via the ideal gas law; with more molecules, less energy is available per molecule);
   • while the efficiency is a complicated function of the given values, it is turns out that, holding all other values constant, increasing P_b or decreasing P_c will increase ε, while the value of V_a does not alter ε at all and the chosen value of P_a is almost optimal.

   Of course, for another cycle, the results can be very different.

   For an air conditioner, heat pump in air conditioning mode, or refrigerator, ε = Q_transferred / W_required. The efficiency of a refrigerator can be greater than 1, since

   ε = Q_c / (Q_h - Q_c)

   = 1 / (Q_h / Q_c - 1),

   where Q_c is the heat removed from the cooler environment and Q_h is the heat exhausted into the warmer environment. Note that Q_h must be greater than Q_c.
5. We often consider a cycle operating between two heat reservoirs (of infinite heat capacity), one at temperature T_h(ot) and the other at temperature T_c(old). For such a device, ΔS includes the engine itself and the reservoirs. Since the engine operates in a cycle, its ΔS is 0, so for isothermal transfers,

   ΔS = - ΔQ_h / T_h + ΔQ_c / T_c.

   In general, ΔS = ∫ dQ / T.

   For the example above, ΔS_b→c = 36.5355 J/K, and of course ΔS_d→a = 0. To compute ΔS_a→b and ΔS_c→d, we use the ideal gas law to express T as a function of P and V:

   ΔS_a→b = ∫ n c_v dT / T

   = ∫ n c_v (V dP / (n R)) / (P V / (n R))

   = n c_v ln (P_b / P_a) = 20.2262 J/K

   and

   ΔS_c→d = ∫ n c_p dT / T

   = ∫ n c_p (P dV / (n R)) / (P V / (n R))

   = n c_p ln (V_d / V_c) = -56.7617 J/K

   The changes in entropy of the reservoirs are of course dependent on their temperatures. Assuming that the isobaric compression lost heat to a reservoir at room temperature (< T_d), and that the isochoric and isothermal processes gained heat from a reservoir at 320 C (> T_b),

   ΔS_{cold reservoir} = 24119.6 / 293.15 J/K = 82.277 J/K and

   ΔS_{hot reservoir} = -31172.9 / 593.15 J/K = -52.555 J/K,

   so that

   ΔS_reservoirs = 29.722 J/K,

   which is greater than zero, as required by the second law of thermodynamics.

   If we did not know T as a function of P and V, it would be necessary to connect each pair of endpoints with a combination of adiabatic and isothermal processes, and compute the change in entropy using those new processes. For example:

   

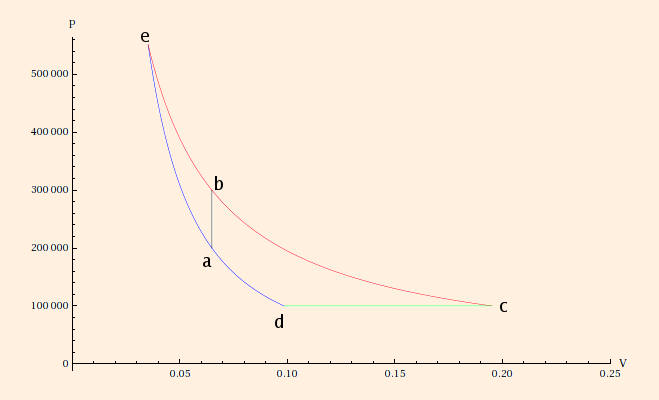
   Process a→e is an adiabatic process, and e→b is isothermal. P_e = 551,135 Pa and V_e = 35.3815 L, from

   P_a V_a^γ = P_e V_e^γ

   = n R T_b V_e^{γ - 1}

   This gives us (using the same equations as above)

   ΔQ_a→e = 0 and

   ΔQ_e→b = 11,859.9 J.

   Since entropy is a state variable,

   ΔS_a→b = ΔS_e→b = 20.2262 J/K,

   as before. Either way, the entropy change of the engine is zero, because it is a cycle: all state variables, including entropy, end at the same state in which they began. Therefore ΔS_c→d = -56.7617 J/K.
6. The Carnot cycle is the most efficient cyclic thermodynamic process conceivable:
   1. isothermal expansion, with ΔQ = Q_h at T_h ;
   2. adiabatic expansion, with T_h→T_c ;
   3. isothermal compression, with ΔQ = - Q_c at T_c ; and
   4. adiabatic compression, with T_c→T_h .

   What makes it so is that each step of the Carnot cycle is reversible: all changes of state are infinitesimally close to equilibrium.

   Reversible changes of state are infinitely long; all real changes of state are irreversible.

   In isothermal processes, by definition the gas is in thermal equilibrium with the reservoir. An adiabatic process can be irreversible:

   Consider a closed, thermally insulated volume with a partition in the middle, such that nearly all of the gas molecules are on one side of the partition; the other side is a nearly perfect vacuum. With removal of the partition, the gas adiabatically but irreversibly doubles in volume.

   A reversible adiabatic process would be a change in volume by infinitesimal steps while the gas is thermally insulated.

   Since it is reversible, the total entropy change of the Carnot cycle reservoirs is zero. This gives us

   0 = - Q_h / T_h + Q_c / T_c

   or

   Q_c / Q_h = T_c / T_h.

   If we attempt to compute the entropy change for c→d by finding a point f on the PV diagram such that c→f is adiabatic and f→d is isothermal, we find that we have constructed a Carnot cycle:
   

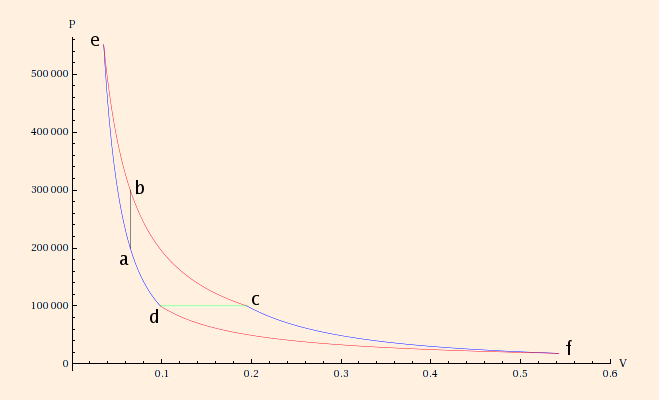
   Hence the total entropy change is zero including the reservoirs, and its efficiency is

   1 - T_d / T_b = 49.4761%.

   The efficiency of a Carnot Refrigerator is T_c / (T_h - T_c).
7. Thermodynamic cycles of practical interest include:
   • the Diesel Engine, consisting of adiabatic compression (a → b), isobaric heating (b → c), adiabatic expansion (c → d) and isovolumetric cooling (d → a);

     ε = 1 - (T_d - T_a) / ((1 + 2 / χ) (T_c - T_b))

   • the Otto Cycle, consisting of adiabatic compression, isovolumetric heating, adiabatic expansion and isovolumetric cooling;

     ε = 1 - (V_small / V_large)^{(2 / χ)}

   • the Stirling Engine, consisting of alternating isothermal and isovolumetric processes.

     ε = 1 / (1 + T_lower / |Δ T| + χ / (2 ln (V_large / V_small)))

   In each case, ε was computed for an ideal gas. Note that in each case, it is independent of n, and increases with decreasing χ. This generalizes what we saw above: if we think of work as the result of increased temperature, less heat input is required to change the temperature of a gas with fewer degrees of freedom.

8. It is important to remember that these are models of real thermodynamic process. In actual physical processes,
   • gasses are never perfectly ideal;
   • n is never constant;
   • nothing has infinite heat capacity; and
   • no process is perfectly adiabatic (or, of course, reversible).

(prev)

(top)

(next)

©2012, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.