Compact Lie Group Cheat Sheet

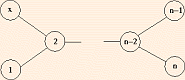
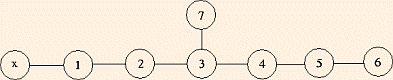
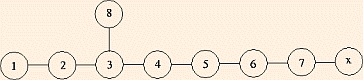
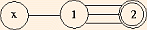
Lie Class	Group	# of generators	isomorphisms	extended Dynkin Diagram	discrete center
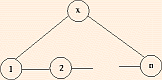
An	SU(n + 1)	(n + 1)2 - 1	A1 ~ B1		Zn + 1
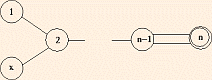
Bn	SO(2n + 1)	n (2n + 1)	B1 ~ C1
Cn	Sp(2n)	n (2n + 1)	C2 ~ B2		Z2
Dn	SO(2n)	n (2n - 1)	D2 ~ A1 + A1		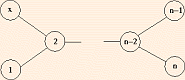Z2
			D3 ~ A3
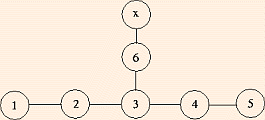
E6	E6	78
E7	E7	133			Z2
E8	E8	248			Z3
F4	F4	52
G2	G2	14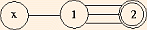

Notes:

1. The rank n is the dimension of the Cartan subalgebra (the maximal Abelian subalgebra), whose eigenvalues in the adjoint representation are the roots.
2. SU(n) leaves invariant the quadratic form z_i zbarⁱ; SO(n) leaves invariant the quadratic form x_i xⁱ; Sp(n) leaves invariant the quadratic form in 2n dimensions x_i x'^{n + 1 - i} - x'_i x^{n + 1 - i}.
3. In the (extended) Dynkin Diagrams, removing a root yields a (maximal) subgroup.

©2008, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.