
The wave number, which is simply the number of cycles per unit length, is somehow more difficult to intuit, even though we have simply replaced time by distance. And the phase angle, while simply a constant angle added to the argument of the sine or cosine function describing the wave, can be even more intimidating.
This applet allows you to visualize the effect of changes in wave number and phase angle:
The horizontal axis extends from -2π to +4π. And if you think of the horizontal axis as time instead of distance, the wave number scroll bar acts as a frequency scroll bar.
This applet allows you to hear beats:
Standing waves are described by their fundamental frequency and mode (an integer starting with 1, which corresponds to the fundamental). Two waves can be in phase, so that they reach their minimum and maximum values simultaneously, or out of phase, so that one reaches its maximum every time the other reaches its minimum, or they can have any relative phase angle.
This applet allows you to view standing waves and superposition of two waves (when turned on, the red wave is the sum of the black wave and the blue wave); the fundamental is fixed, but boundary conditions, modes and relative phase angles are adjustable:
Note that the blue wave is drawn after the black one, so that if they have the same mode and are in phase, you will only see the blue one. Also notice that if the boundary conditions are not the same at each end, only odd integer modes are allowed.
This applet allows you to visualize constructive and destructive interference in waves from two sources (located at bottom center):
These applets allow you to view diffraction patterns; the first shows a visual approximation of the pattern, and the second plots the intensity at the screen.. Wavelength and experimental geometry can be varied.
But for a concave mirror (looking into the inside of the spherical segment), something very interesting happens. It turns out that the magnification M is given by
M = 1 / (1 - 2 O / r)where O is the distance from the object to the surface of the mirror. M is still 1 when the object touches the mirror, and the image is still right-side-up. But as the object recedes toward a distance r/2 from the mirror, the magnification approaches infinity (here, r = 2m):
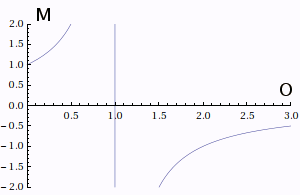
As the object continues to recede, the image is inverted (M < 0), and slowly shrinks in magnification. Try this with the inside of a highly polished serving spoon, or some other reflecting concave surface.
©2013, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.