Postscript: Extraterrestrial Life

Discussions of life on other worlds usually include Drake's Equation:

number of technological civilizations in the galaxy =
rate of star formation * fraction of those with planets * number of habitable planets *
fraction with any life * fraction of those with intelligent life * fraction of those with technology *
lifetime of a technological civilization

As you can see, computing the number of technological civilizations in the galaxy is largely an exercise in guesswork, Most sources choose values for the various factors so that, in effect, the equation becomes

number of technological civilizations in the galaxy ~ lifetime of a technological civilization

Let us ask a more tractable question: how many planets are there in the galaxy which harbor any life at all? We will need to take into account the following:

Planets too close to the galactic core will receive too much radiation and cosmic ray flux for life to develop. If the central bulge has a radius of 3 kpc, it seems reasonable to expect that life-bearing worlds would be at least twice that far from the core.

The stars at the edge of the galaxy are older and do not contain enough of the heavier elements required for life; there simply haven't been enough generations of stars. We will assume that the outer 3 kpc of the disc is too old.
That leaves an annulus (a disc with a circular hole in the center) of inner radius 6 kpc and outer radius 12 kpc, or roughly
π (12² - 6²) / (π 15²)
= 48 %
of the galactic disc which may contain stars with habitable planets. Since the central bulge contains about 30% of the luminous matter in the galaxy, this means that only about 1/3 of the stars in the galaxy may have habitable planets.

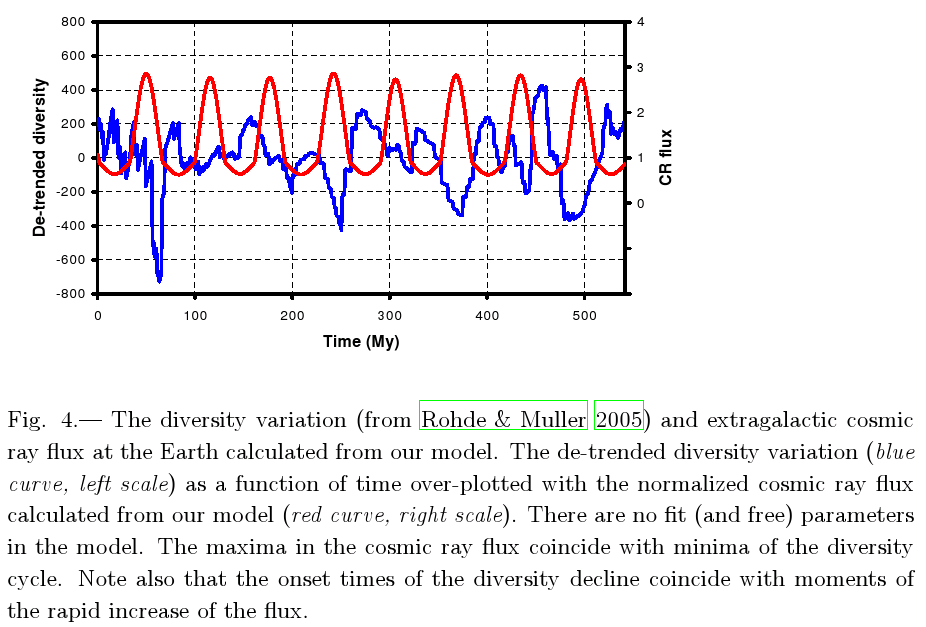
In their paper "Do extragalactic cosmic rays induce cycles in fossil diversity?", Medvedev and Melott model the variation of cosmic ray flux as the solar system moves in and out of the galactic plane, and relate it to variations in biodiversity on Earth:

Cosmic ray flux and biodiversity on Earth. (source)

This indicates that planets lying too far out of the plane of the galactic disc may also receive too much radiation and cosmic ray flux for life to develop. The Sun is currently about 10 pc north of the galactic plane, and moves as far as 70 pc above or below it with time. Assuming that the central half of this variation is compatible with life (70 pc), and that the thickness of the disc is about 150 pc, this reduces our third of eligible stars to about 16%.

Planets around binary systems should have orbits too unstable for life to develop. Since about 75% of all stars are members of a binary system, we are down to about 4% of the stars in the galaxy which we would expect to have habitable planets.

Life arose on the Earth about 1 billion years after the Sun entered the main sequence. Any planet with life should probably orbit a star which has been on the main sequence at least 1 billion years.

Liquid water appears to be necessary for life. All life that we know is characterized by the following statement: life is the maintainence of concentration gradients across membranes. Water is the medium in which the chemicals necessary for life are dissolved; the membranes are the walls of cells, and the concentrations of those chemicals on either side of the cell walls is different. When the concentrations become the same and stay that way, the cell is in static equilibrium with its environment, and activities associated with living terminate. There are anhydrobiotic organisms (which can survive without any water in their bodies), but in the dessicated state, they simply lie inert until they are re-hydrated.
So in order for a planet to develop life, it is necessary for liquid water to exist there. We can use the following relationships to estimate the "water zone" around a star of a given mass. From the relation
stellar lifetime_years = 10¹⁰ / mass_solar^2.5
and our last consideration, the star's mass has an upper limit of about 10^1/2.5 = 2.5 M_solar. Since less than 1% of stars have a mass in excess of 2.5 M_solar, we can safely ignore this limit here.
Because luminosity is approximately equal to mass^3.5 (in solar units), the energy flux received by the planet will be
energy flux = luminosity / (4 π distance²)
= M_solar^3.5 L_solar / (4 π distance²)

Assuming that the planet has surface water, its temperature must be between the freezing and boiling points of water: 273 and 373 K. Stefan's Law tells us that in equilibrium (another assumption, but reasonable), the energy flux should be equal to the
power emitted per unit area = σ * temperature⁴
so the flux received from its star should be between
σ 273⁴ = 315 W / m²
and
σ 373⁴ = 1097 W / m²
Our Earth obviously violates this bound, but we have not taken into account atmospheric effects. Since the average surface temperature of the Earth is 288 K, and we receive about 1365 W / m² from the Sun, we can estimate that the presence of an atmosphere alters these numbers by the factor
1365 / (σ * 288⁴) = 3.5
to give us 1100 and 3840. Setting our expression above for the energy flux equal to these two values, we find that the orbital distance (semimajor axis length) should be between
(M_solar^3.5 L_solar / (4 π 1100))^1/2
= M_solar^1.75 * 1.67 * 10¹¹ m = 1.12 AU * M_solar^1.75
and
(M_solar^3.5 L_solar / (4 π 3840))^1/2
= M_solar^1.75 * 8.93 * 10¹⁰ m = 0.6 AU * M_solar^1.75
If we consider our Solar System to extend out to the orbit of Neptune, at 30 AU, and assume that is a typical size, this implies that habitable planets would only be found in an annulus representing about
π (1.12² - 0.6²) / (π 30²)
= 0.1 %
of the Solar System's volume. Since Earth is one of eight planets in the Solar System, we might reasonably guess that about one in a hundred stars has a habitable planet in orbit. Since there are about 100 billion stars in our galaxy, and we have estimated that 4% of them might be eligible to have a habitable planet, but only 1% of those do, we conclude that in our galaxy alone, there are about 40 million worlds with life of some kind.

Since there are approximately 100 billion galaxies in the universe, and about 3/4 of them are spirals, we might expect there to be as many as 3 quintillion planets with life in the universe. Does this number have any basis in fact? We have made a number of educated guesses in this analysis, but it seems fairly obvious that, depending on your definitions, the universe is teeming with extraterrestrial life.

This study indicates that 20% of the stars in our galaxy have habitable planets. If that is true, our analysis is low by a factor of 5.

Please send comments or suggestions to the author.