Stellar Evolution

Stellar Evolution (I)

stellar lifetime_years = 10¹⁰ mass_solar / luminosity_solar

Since luminosity is approximately equal to mass^3.5 (in solar units), this is equivalent to

stellar lifetime_years = 10¹⁰ / mass_solar^2.5

leading us to the conclusion that more massive stars burn out more quickly.

We will continue to use the common term "burning" for the nuclear reactions which power stars. But it is important to understand that stars are not "on fire": there is no organic material to be oxidized, and not much Oxygen to do the oxidation.

These graphs illustrate the lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, from various perspectives (use the Shift key to expand them):

	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, relative to the end of the main sequence phase of a 0.5 solar mass star; scale = 31 billion years.
	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, relative to the lifetime of a 1 solar mass star; scale = 12 billion years.
	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, relative to the lifetime of a 1.5 solar mass star; scale = 2.5 billion years.
	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, relative to the lifetime of a 3 solar mass star; scale = 350 million years.
	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, relative to the lifetime of a 5 solar mass star; scale = 90 million years.
	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, relative to the lifetime of a 9 solar mass star; scale = 35 million years.
	The lifetimes of stars of 0.5, 1, 1.5, 3, 5 and 9 solar masses, showing the birth of a 9 solar mass star; scale = 1 million years.

The brown phase represents the Hyashi Track, during which the protostar shrinks significantly, dropping in luminosity but increasing in temperature due to the increased internal pressure. At the beginning of the Hyashi Track, the core is convective. For stars less than 1.3 solar masses, the core is radiative by the end of the track, and the pp chain dominates the fusion reactions that begin then. For stars greater than 3 solar masses, the core is convective throughout and the CNO cycle dominates.

The green phase represents the approach to equilibrium that precedes the main sequence. During this phase, the outward pressures from the fusion reactions in the core have not come into equilibrium with the gravitational pressures tending to contract the star, resulting in winds significantly larger than those generated by a main sequence star.

The time of the beginning of the main sequence (shown in yellow) is called the Zero Age Main Sequence. A star arrives on the main sequence then, and stays essentially at that one place on the H-R diagram as long as it continues to fuse Hydrogen into Helium in its core.

What happens next is a tug of war between the opposing pressures due to fusion and gravity: as fusion products build up in the core, its density increases. The core shrinks, the pressure increases, the temperature increases, heavier nuclei begin to fuse in the core and previous fusion reactions move outward into shells. As the fusion reactions take place in regions closer to the surface of the star, the outward pressure from those reactions enlarge the star. Depending on the size of the star, this process can repeat, with multiple shells supporting different reactions simultaneously.

The period of Hydrogen shell burning is shown in orange, and the red giant branch is shown in red. During this portion of stellar evolution, the star's luminosity and radius increase enormously, but the expansion is cooling and results in a drop in surface temperature.

At the end of the red giant branch, if the star is less than 0.5 solar masses, no Helium fusion occurs. If the star is less than 2.25 solar masses, the Helium core has already begun to collapse into a degenerate state, and there is a Helium flash which begins Helium fusion. Larger stars begin burning Helium in a smooth transition.

The change in stellar radii as from the beginning of the main sequence to the end of the red giant branch; the black vertical line indicates 1 A.U; the vertical axis is mass.

The horizontal branch is shown in purple. This is another equilibrium state, during which the star's luminosity is almost constant. Its surface temperature and radius may change depending on the nuclear reactions underway. For stars greater than 4 solar masses, Carbon fusion also occurs during the horizontal branch (and a Carbon flash can occur). For stars greater than 8 solar masses, Oxygen fusion also occurs, and for stars larger than 10 solar masses, Silicon burning occurs in the terminal stages before supernova.
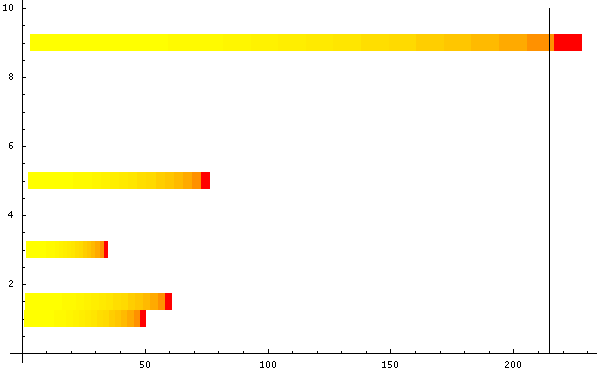
The fusion of successively heavier nuclei is an accelerating process, due to the drop in the number of nuclei available to fuse. Carbon fusion might last for hundreds of years before Oxygen fusion begins, but Oxygen burning might last only a year or so before Silicon fusion begins. It takes about a day for the core to fuse into Iron.

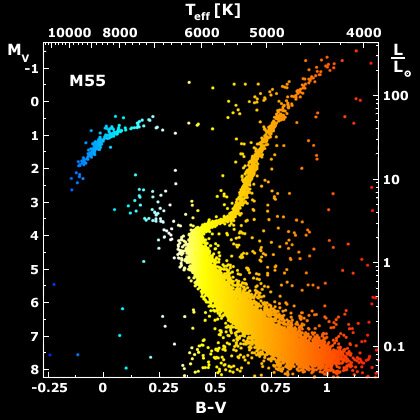
By examining an H-R diagram for the stars in a globular cluster like M 55, it is possible to determine the age of the cluster:

H-R diagram for M 55. (source)

Since more massive stars have shorter lives, the "end" of the main sequence tells us how old the cluster is. Compare visible and ultraviolet images of the cluster Omega Centauri; note the obvious population differences between hot and cooler stars:

Omega Centauri in visible and UV. (source)

Numerical values in this section are approximate. Stellar life cycles are based on models described in 1965 and 1967 by Iben (Astrophysical Journal 141:993 and Annual Reviews of Astronomy and Astrophysics 5:571, respectively).

Stellar Evolution (II)

White Dwarfs

The final fate of a star depends on its mass at the termination of fusion processes. Stars born with less than 8 solar masses experience a series of Helium shell flashes which cause the luminosity to fluctuate and the outer layers to be ejected, forming a planetary nebula. These stars typically shed enough mass so that their final mass is less than the Chandrasekhar Limit of 1.44 solar masses to become a white dwarf: the compressed core of the final fusion product.

Note the shapes of the nebulae in these images; the processes which create them must be far less symmetrical than the naive spherical stellar model which all our discussion of radii imply:

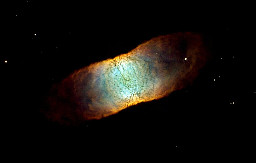	IC 4406; probably cylindrical, seen from the side (R, G, B = Nitrogen, Hydrogen, Oxygen).	source
	NGC 6543: The Cat's Eye Nebula.	source
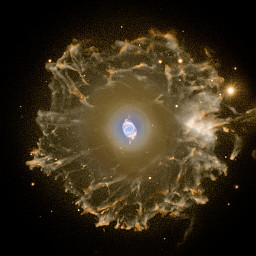	The extended halo of the Cat's Eye Nebula.	source
	HD 44179 appears to be a binary system nearing the end of its life.	source
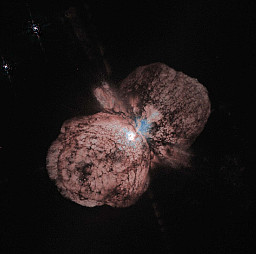	Eta Carinae, shedding mass.	source
	NGC 2440 (R, blue-green, B = Nitrogen/Hydrogen, Oxygen, Helium).	source

A white dwarf is a degenerate star because its atoms are as close as possible within the constraints of the Pauli Exclusion Principle, which tells us that no two electrons can be in the same state. In this condition, every atom is in the lowest state possible, so that the number of available states, or degeneracy, is as low as possible.

Sirius B is a white dwarf whose absolute magnitude is 11.2 and whose mass is approximately equal to that of our Sun. Its luminosity is then

L = 10^{(4.83 - M)/2.5}
= 10^-2.548 = 0.0028 L_solar

Its black body temperature is around 14,800 K, so its radius is

r = (L / (4 π σ T⁴))^1/2
= (0.0028 * 3.84 * 10²⁶ / (4 π σ 14800⁴))^1/2
= 5.61 * 10⁶ m = 0.008 R_solar

From this we can compute its average density

ρ = m / (4/3 π r³)
= 2 * 10³⁰ / (4/3 π (5.61 * 10⁶)³), times 0.001 to convert kg/m³ to g/cm³,
= 2.7 * 10⁶ g / cm³ (!)

and its escape velocity

escape velocity = (2 * G * mass / radius)^1/2
= (2 * G * 2 * 10³⁰ / 5.61 * 10⁶)^1/2
= 6.88 * 10⁶ m/s
= 0.023 c.

Its surface gravity is

surface gravity = G * mass / radius²
= G * 2 * 10³⁰ / (5.61 * 10⁶)²
= 4.22 * 10⁶ m / s²,

which means that if you could survive on its surface, you would weight about 430 thousand times as much as you do on Earth! These values are typical orders of magnitude for white dwarfs:

White Dwarf	Absolute Magnitude	Mass_solar	Radius_solar
40 Eridani B	11	0.501	0.0136
Procyon B	13.2	0.604	0.0096
Sirius B	11.2	1	0.0084

(source)

Note that at 8.6 light years, Sirius B is the closest white dwarf to Earth. That, coupled with the fact that it is a binary partner to Sirius A, allows us to understand it much better than many other white dwarfs. Careful observation of their orbital period and separation was the key to computing its mass.

Neutron Stars

Stars born larger than 8 solar masses usually retain enough mass to undergo core collapse, with the resulting shock wave producing a Type Ib supernova (spectra without Hydrogen or Silicon lines, with Helium lines), a Type Ic supernova (without Hydrogen or Helium or Silicon lines) or a Type II supernova (with Hydrogen lines). The presence of specific lines in their spectra probably indicates which outer layers were blown off before the explosion occurred. These supernova types can also be classified by their light curves, which show their energy output (here in the blue band) as a function of time:

Supernova light curves.

For Type II supernovae, the "-P" and "-L" designations stand for "plateau" and "linear". The timings of the light curve decays seem correlated with the radioactive decay rates of ⁵⁶Ni and ⁵⁶Ni.

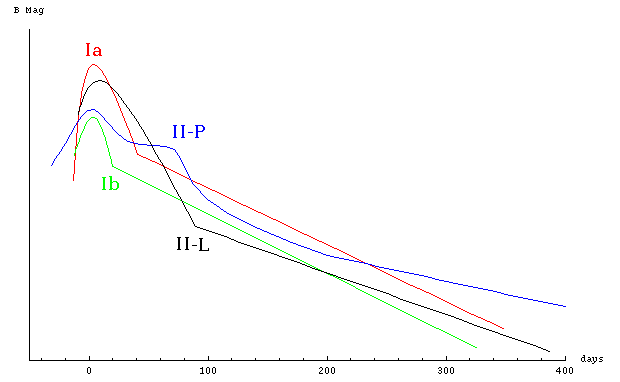
If the final mass at core collapse (after the shells have been shed) is less than 3-3.2* solar masses, the remnant will be a neutron star. In a neutron star, the atoms have come so close to each other that the electrons have been absorbed into the nuclei, releasing neutrinos. The remaining neutrons are now degenerate: they are as close as possible within the constraints of the Pauli Exclusion Principle. A neutron star is essentially one large, extremely dense nucleus, with no net electric charge.

*Most neutron star masses are close to 1.4 M_solar; the largest measured so far is about 2.1 M_solar. The actual limit depends on how neutron matter behaves, and is the subject of ongoing research.

If the neutron star is rotating, and has a sufficiently large magnetic field whose axis is not along the rotation axis, we may observe it as a pulsar. It is assumed that most if not all stars rotate, so by conservation of angular momentum, a collapsed core such as a white dwarf or neutron star will rotate much faster than its progenitor, by a factor of

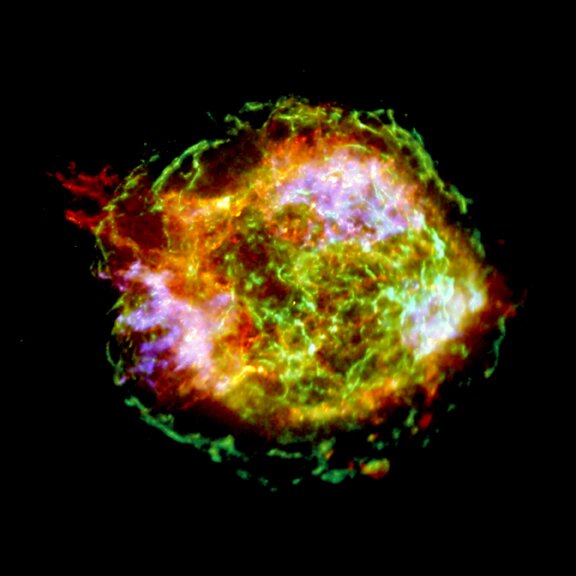
(r_before / r_after)².

The neutron star at the heart of the Crab Nebula has about 1.4 times the mass of Sirius B but its radius is only about 10 kilometers. This is 560 times smaller, so its density is 250 million times larger, its escape velocity is 28 times larger (0.64 c) and its surface gravity is 440 thousand times greater! We have already seen the Crab Nebula in multiple wavelengths; here is an x-ray image of the neutron star and supernova remnant Cassiopeia A:

Neutron star and supernova remnant Cassiopeia A, in x-rays. (source)

Planetary nebulas glow from irradiation by the remnant white dwarf or neutron star.

Now consider our old friend Betelgeuse. As we mentioned in previously, it is an M2Ib star located 427.3 light years from us. Its temperature is about 4000 K, its mass is about 20 M_solar and its luminosity is about 50,000 L_solar. That means that its radius is

r = (50000 * 3.84 *10²⁶ / (4 π σ 4000⁴))^1/2
= 3.25 * 10¹¹ m = 464 R_solar

Since its luminosity is varying, we know it is in the horizontal branch, and it is estimated that within 10,000 years it will explode as a supernova. Assuming the supernova has a peak luminosity of 10¹⁰ L_solar, the energy flux we should experience here on Earth is

energy flux = luminosity / (4 π distance²)
= 10¹⁰ * 3.84 *10²⁶ W / (4 π (427.3 ly * 9.461 * 10¹⁵ m/ly)²)
= 0.0187 W/m²

This may not seem like much compared to the total flux we receive from the Sun, but consider that much of this is in gamma radiation. If we assume the normal gamma flux is 5 MeV/cm²/s, or around 8 * 10^-9 W/m², this is a lot of radiation. The lesson here is that the neighborhood affected by a supernova is very large. In any given galaxy, every 30 to 50 years another star explodes as a supernova:

SN 1994D in NGC 4526. (source)

This makes the universe seem like a violent place, and it can be. But it is important to remember that the explosion of a supernova not only disrupts its neighborhood, but it also seeds the interstellar medium with heavier elements, and the shock waves compress that medium so that more stars can develop in the future:

Henize 206. (source)

Star forming regions in galaxies are identified by the hydrogen gas glowing in infrared and by the ultraviolet light of young, bright stars.

Please send comments or suggestions to the author.