Distance vs. Direction

Because the universe is so vast, many of the distance units we use are based on the travel time of the fastest thing there is: light. The speed of light in vacuum is

c = 299,792,458 meters per second
= 2.998 * 10⁸ m/s.
(Scientific notation, using exponents, are ubiquitous in physics; the scope of our inquiry demands their use.)

The distance in meters can then be computed using

distance = velocity * time.

So, for example, one lightsecond is 2.998 * 10⁸ m. We will find the following distance units useful:

One Astronomical Unit (AU) is the average radius of Earth's orbit, equal to 1.496 * 10¹¹ meters (m).
One lightyear (ly) is the distance light travels in a vacuum in one year, equal to 9.461 * 10¹⁵ m.
One parsec (pc) is the distance to a star whose parallax angle is one arcsecond; 1 pc = 3.086 * 10¹⁶ m = 3.262 ly.

Here are some images which might help you appreciate the orders of magnitude involved in our study:

	1 meter is a little more than a yard; the solar arrays on the International Space Station span a distance of 78 meters.	source
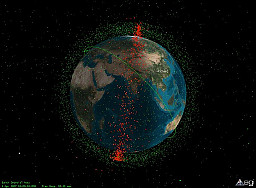	1 kilometer is about 0.6 miles; the ISS orbits at a distance of 400 km above Earth's surface (the dots are orbital debris).	source
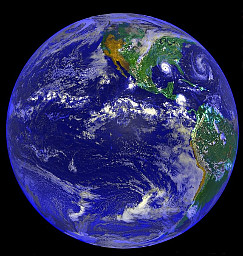	1000 kilometers is about 1/6 of the radius of the Earth.	source
	1000 kilometers is a little over half of the radius of the Moon.	source
	1 lightsecond is about the distance to the Moon.	source
	1 lightminute is about 1/8 of the distance from the Earth to the Sun (here seen in ultraviolet light).	source
	1 lighthour is about the distance from the Sun to a point midway between Jupiter and Saturn.	source
	1 lighthour is about the distance from the Sun to a point midway between Jupiter and Saturn.	source
	1 lightday is about 4 times the distance from the Sun to Pluto.	source
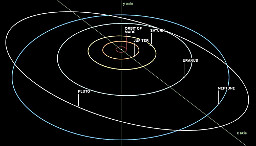	The scale of the orbits of the outer planets is in lighthours.	source
	1 lightweek is approximately the average distance between stars in the central part of NGC 3949, a galaxy very similar to our own Milky Way.	source
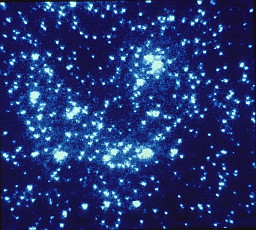	1 lightmonth is approximately 2 times the average distance between stars in a globular cluster like 47 Tucanae.	source
	1 lightyear is about 1/4 the distance to the nearest star (after Sol), Alpha Centauri. 1 parsec is about 3/4 of that distance.	source
	The globular cluster M 80 is about 8 parsecs wide.	source
	10 parsecs is about the distance to Gliese 436b, an extrasolar planet, known to us by the wobble its orbit induces in its parent star.	source
	100 (10^2) parsecs is about 3/4 of the distance to Betelgeuse.	source
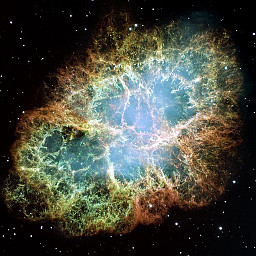	1000 (10^3) parsecs is about 1/2 the distance to the Crab Nebula.	source
	10,000 (10^4) parsecs is about the distance to the center of the Milky Way.	source
	100,000 (10^5) parsecs is about twice the distance to Supernova 1987A, in the Large Magellanic Cloud.	source
	1 megaparsec (10^6 parsecs) is about the distance to M 31 in Andromeda, at the other end of the local group of galaxies	source
	This portion of the Coma Cluster of galaxies is about 1 megaparsec across (the whole cluster is about 8 megaparsecs across).	source
	10 megaparsecs is about the distance to M 104 in the Virgo Cluster of galaxies.	source
	100 megaparsecs is about the distance to Stephan's Quintet of interacting galaxies.	source
	1000 megaparsecs is about 3/4 of the distance to CL 0939+4713, a remote galaxy cluster at z = 0.4.	source
	The lumpy objects in this image are probably protogalaxies at z > 1.	source
	Abell 2218 is a galaxy cluster containing objects up to z = 7 (red streaks at upper left).	source

"NGC" stands for New Galactic Catalog, and objects designed by "M" followed by a number from 1 to 110 are Messier Objects, cataloged by Charles Messier in the latter part of the 18^th century.

(View Cosmos DVD 6, episode 10, Milky Way Simulation and Large Scale Structure Images.)

Parallax

The parallax of the red star is larger than the parallax of the gold star.

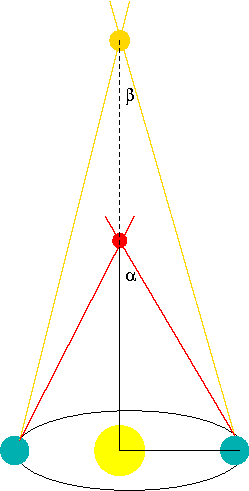
The two blue-green circles represent the Earth at opposing points in its orbit. The large yellow circle between them of course represents Sol (our Sun). Suppose we want to measure the distances to the red and gold stars. As the Earth moves over half its orbit, each star appears to change position. This is called parallax and the change in position is twice the parallax angle. The parallax angle for the red star is α and that for the gold star is β. β is less than α because the gold star is farther away.

If we know the radius r of the Earth's orbit we can compute the distances R_i to the stars:

R_red = r cot (α) and R_gold = r cot (β)

Since for large distances cot(θ) is very close to 1/θ (if θ is measured in radians!), we have

R_red = r / α and R_gold = r / β

A parallax angle of 1 arcsecond yields a distance of 1 parsec (there are 360 degrees around a circle, 60 minutes of arc in a degree and 60 seconds of arc in a minute). Therefore to find the distance in parsecs of a star whose parallax is measured in milliarcseconds (mas), simply divide 1000 by the parallax.

The Partial Perspective Viewer

will help you find your place in the universe (with a very fond wink at the shade of Douglas Adams):

This applet knows where some things in the universe are, and will display their locations in 3D. You may change the orientation by dragging on the image: horizontal dragging rotates about the z axis, verticle dragging tilts the z axis. You may change the distance scales using the "Zoom In" and "Zoom Out" buttons below. The Milky Way Galaxy is identified at its center. Earth (representing the entire solar system) is drawn in green. Even though there is no "center" of the universe, Earth is drawn for convenience at the origin of the graph.

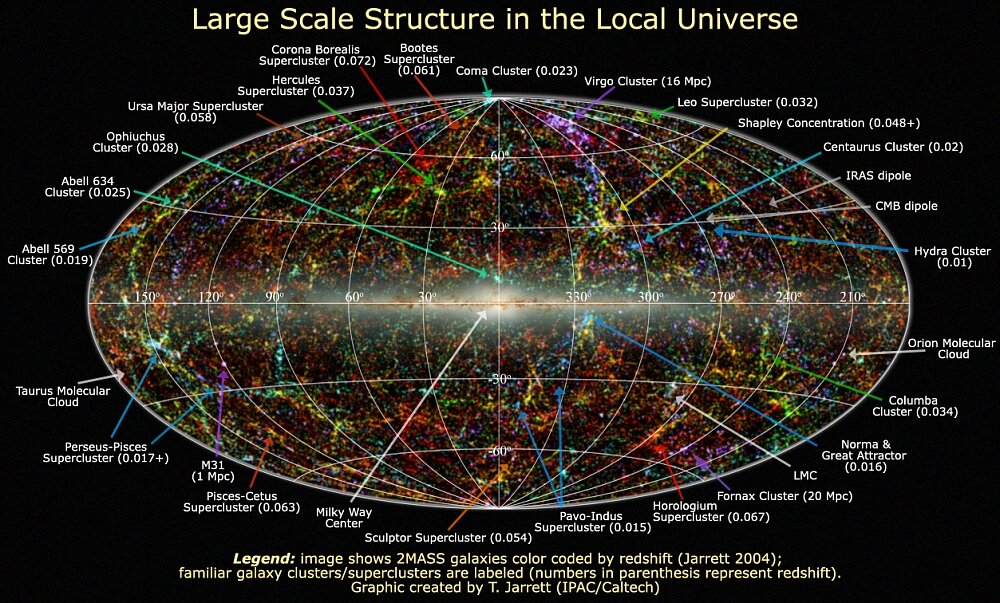
You need a Java-capable browser to be able to use the applets. If they do not work with your Windows system, download the Java VM (Virtual Machine) for your version of Windows at the download section at java.sun.com.

As you zoom out into the furthest reaches of the universe, you will notice a "dust" of unlabeled dots. Each dot is a cluster of galaxies, from the Abell Catalog. Some Abell clusters have been labeled, but most are not for the sake of clarity.

2MASS, the 2 Micron All Sky Survey, permits us to see the nearest million and a half galaxies all at once. (source)

Portfolio Exercise: If we adopt a scale of 1 cm to represent 1 lightsecond, then 1 foot would represent 30.5 lightseconds and 1 mile would represent 160934 lightseconds, or 1.86 lightdays.
If we imagine the Sun to lie at mile marker zero on I-75 in Florida, how far from that point would the Earth lie? The midpoint between Jupiter and Saturn? Pluto?
I-75 is 467 miles long in Florida; 353 miles long in Georgia; 160 miles long in Tennessee; 192 miles long in Kentucky; 210 miles long in Ohio; and 394 miles long in Michigan. Where along I-75 would you locate Alpha Centauri?
To deal with the rest of the universe, we obviously need a different scale. Let us now use 1 inch to represent 1 parsec. Then 1 mile would represent 63360 parsecs. Where along I-75 (using this new scale) is Betelgeuse? The Crab Nebula? The center of the Milky Way? Supernova 1987A? M31? M104? Stephen's Quintet? Place these seven objects as accurately as possible on this map of I-75 and include it in your portfolio.

The Changing Cosmos

We rarely see change as we observe the distant cosmos, supernovae being the obvious exceptions.

This time lapse of M3 over a single night shows one of the few phenomena that are observable on human time scales: variable stars of the RR Lyrae type. (source)

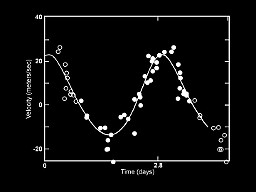
RR Lyrae is a star in the constellation Lyra. It is a variable star, whose luminosity changes regularly with time as it fuses Helium in its core. Its distance is known because it belongs to a cluster whose parallax is known. Since stars of its type have a well-defined relationship between their luminosity and the period of their variability, they are useful standard candles: objects whose behavior dictates their luminosity. This, as we will see, can be compared to their apparent brightness to determine their distance.

This sequence of the Cat's Eye Nebula shows the expansion of the nebula over a 3 year period. (source)

Orion - What you see and where things really are

The constellation Orion; the red line represents the celestial equator, and the white line represents 6 hours Right Ascension.

The stars are labeled with Greek letters (in order, "alpha", "beta", "gamma", "delta", "epsilon", "kappa" and "zeta") indicating their relative brightness within the constellation; their common names, celestial coordinates, visual magnitude, parallax, distance and spectral classes are given here:

Name	Common Name	RA	dec	mag	Parallax (mas)	distance (ly)	Spectral Class
α Orionis	Betelgeuse	05 55 10.29	+07 24 25.3	0.45	7.63	427.3	M2Ib
β Orionis	Rigel	05 14 32.27	-08 12 05.9	0.18	4.22	772.5	B8Ia
γ Orionis	Bellatrix	05 25 07.87	+06 20 59.0	1.64	13.42	242.9	B2III
δ Orionis	Mintaka	05 32 00.40	-00 17 56.7	2.25	3.56	915.7	O9.5II+
ε Orionis	Alnilam	05 36 12.81	-01 12 06.9	1.69	2.43	1341.6	B0Ia
κ Orionis	Saiph	05 47 45.39	-09 40 10.6	2.07	4.52	721.2	B0.5Iavar
ζ Orionis	Alnitak	05 40 45.52	-01 56 33.3	1.74	3.99	817.0	O9.5Ib SB

This data comes from the Hipparcos Catalog. Note that the common names are all of Arabic origin. Alpha Orionis is a semi-regular pulsating star, gamma and kappa Orionis are variable stars, delta Orionis is an eclipsing binary and zeta Orionis is a double star.

This photograph of the Eastern horizon was taken in the early hours of a mid-October morning in 2002. It is a composite of several 8 second exposures taken with a Canon G1 (in Cincinnati, it takes a little over 10 seconds for the Earth to rotate enough to cause a star to start to become a streak).

Note the tilt of the celestial equator, which is the projection of the Earth's equatorial plane into the sky: 23.45 degrees because of the tilt of the Earth's axis of rotation. The declination (dec) measures "celestial latitude" relative to the celestial equator and is measured in degrees. Comparing the labeled image with the table below, we can see that positive declinations are above the equator, and negative declinations are below it.

Also note that the Right Ascension (RA) increases from right to left; this is because angles increase in counterclockwise rotation, which when looking toward the South is from West to East. The Right Ascension is measured in hours (24 hours is a circle, so there are 15 degrees per hour).

We will discuss magnitude and spectral class later, but there is one very important thing to notice about the table: the distances in lightyears. The constellation Orion looks like it does to us only in a small neighborhood of the Earth. Since the stars are at widely varying distances, any significant shift in position will change the angles between them, and the constellation will appear much different. You can use the Partial Perspective Viewer to get an idea of how this works: try zooming out to 10^2.5 parsecs and tilting the z axis. From that perspective, Rigel, Mintaka, Saiph and Alnitak form a trapezoid obviously disconnected from the others.

Here is a deeper view of Orion (and check out this image of Barnard's Loop).

Portfolio Exercise: Use SIMBAD to find the celestial coordinates of the five brightest stars in the constellation Cassiopeia (α through ε Cas). On a piece of graph paper, set up a coordinate system where the horizontal axis runs from 0 to 2 hours of Right Ascension, and the vertical axis runs from 55 to 65 degrees of declination. Plot the locations of the five stars. Find the constellation in the night sky and use your graph to identify the stars. How do you have to orient your graph so that it looks correct? Why did you have to orient it that way?

Astronomical Distances

Light transit time and parallax are just two of a number of methods for measuring astronomical distances; we will discuss several in more depth later:

technique	equation	approximate maximum effective distance
radar ranging	d = c * echo time / 2	Solar System
stellar parallax	d_pc = 1000 / parallax_mas	200 pc
H-R Diagram (main sequence spectral class determines absolute magnitude)	d_pc = 10^{(mag - Mag + 5)/5}	5000 pc
RR Lyrae / Cepheid Variables: Period/Luminosity relation, calibrated to known distance to Cepheids in the Large Magellanic Cloud	Mag ~ 1.608 * period_days^0.275	20 Mpc (~ Virgo Cluster)
Tully-Fisher Relation: absolute magnitude of a spiral galaxy (a and b depend on morphological type and wavelength)	Mag = a - b Log (width of spectral line)	100 Mpc
Type Ia Supernovae: C-O White Dwarfs explode with characteristic luminosity as a function of their light curves	d_pc = 10^{(mag - Mag + 5)/5}	1000 Mpc
Hubble Relation between distance and recessional velocity	d = v / H₀	z = 1

There are numerous variations on these themes, some involving very clever uses of statistics which are beyond the scope of this text.

All of the techniques based on luminosity measurement depend on our knowledge of the extinction: how interstellar and intergalactic dust and gas absorb light.

Note that these techniques must be calibrated to each other: radar ranging is necessary to accurately determine 1 AU, which is needed for stellar parallax, which is used to calibrate the magnitude-distance relation, etc.

Each technique has limits to its accuracy, for some approaching 20%, and they should in principle all agree where they overlap. At present that agreement is better than 10%. That it is not zero is a testament to the difficulty of consistently measuring many of these quantities.

The maximum distance for the Hubble Relation is listed as "z=1". This refers to the red shift, about which more later.

Please send comments or suggestions to the author.