Electromagnetic Waves

The light you see,
the infrared (literally, "below red") radiation that warms you,
the ultraviolet (literally, "beyond violet") rays that sunburn you,
the radio waves that carry your music and television signals and the
x-rays used to diagnose medical conditions,

are all forms of electromagnetic radiation. They are all waves: periodic functions of space and time. The length of a spatial period is called the wavelength and is denoted λ. The inverse of the temporal period is called the frequency (denoted ν) and is measured in cycles per second, or Hertz (Hz). All of these waves propagate at the speed of light (c), and for our purposes, obey the simple dispersion relation

c = wavelength * frequency

This applet might help you to better visualize waves. You can choose sine waves or cosine waves; the number on the left is just 2π, and shows you the scale of the plot. If you think of the horizontal axis as distance, then you are seeing wavelengths. If you think of it as time, you are seeing periods. The wave number is the number of waves that fit in a given length or time, and the phase angle determines what happens at the origin. As you can see, higher wave numbers give you smaller wavelengths and higher frequencies:

You need a Java-capable browser to be able to use the applets. If they do not work with your Windows system, download the Java VM (Virtual Machine) for your version of Windows at the download section at java.sun.com.

All of these types of electromagnetic radiation consist of changing electric and magnetic fields, and differ only by their wavelength (or frequency):

radiation	λ	ν (Hz)	energy (eV)	source
radio	> 1 m	< 3 * 10⁸	< 1.24 * 10^-6	low-energy atomic or molecular motions
microwave	> .1 mm	< 3 * 10¹²	< .0124	rigid molecular motions
infrared	> 7000 Angstroms	< 4.3 * 10¹⁴	< 1.78	molecular bond motions
visible light	> 4000 Angstroms	< 7.5 * 10¹⁴	< 3.1	atomic electron transitions
ultraviolet	> 50 Angstroms	< 6 * 10¹⁶	< 248	atomic electron transitions
x-rays	> .03 Angstroms	< 10²⁰	< 414 K	electron transitions in heavy atoms
gamma rays	< .03 Angstroms	> 10²⁰	> 414 K	nuclear decays

An Angstrom (A) is 10^-10 meters. An electron-volt (eV) is 1.602 * 10^-19 Joules (a 60 Watt light bulb uses 60 Joules of energy every second).

The energy column corresponds to the energy of a single photon: the smallest amount of radiation possible. The energy (in eV) of a photon of frequency ν is

energy_eV = h * frequency / e,

where h is Planck's Constant (6.626 * 10^-34 Js) and e is the number of Joules in an eV.

The terms "near" and "far", when applied to ultraviolet and infrared wavelengths, indicate how close they are to the visible wavelengths.

Photons from the near-infrared to x-rays are produced when an atomic electron moves from one energy level to a lower one. The characteristic red color seen in many nebulae is due to the Hydrogen-α transition of an electron from the third to the second energy level, with emission of a 6563 A photon:

Infrared radiation of lower energy results from internal molecular vibrations (in these examples, of triatomic molecules):

Observation in multiple wavelengths

What do these other wavelengths tell us? Consider these images ("R", "G" and "B" stand for Red, Green and Blue, respectively):

	M 31 (the galaxy in Andromeda) in optical light.	source
	M 31 in infrared, R = 80,000 A, B = 36,000 A with star light subtracted.	source
	M 31 in ultraviolet, R = 1750-2800 A, B = 1350-1750 A.	source
	M 31 in x-ray, R = 12.4-24.8 A, G = 6.2-12.4 A, B = 3.1-6.2 A.	source
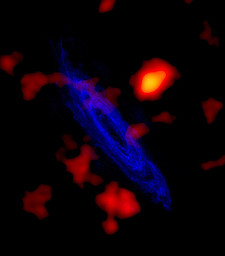	M 31 in radio, 21 cm (2,100,000,000 A).	source
	M 104 in optical.	source
	M 104 in infrared, R = 80,000 A, Orange = 58,000 A, G = 45,000 A, B = 36,000 A.	source
	M 104 in xray, Orange = 8.3-41.4 A, B = 1.8-8.3 A.	source
	NGC 5128 (Centaurus A) in optical.	source
	NGC 5128 (Centaurus A) in infrared, 36,000-80,000 A.	source
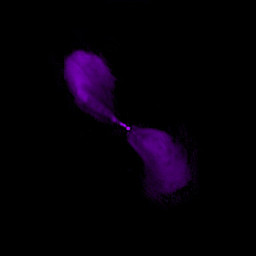	NGC 5128 (Centaurus A) in radio, 20 cm.	source
	NGC 5128 (Centaurus A) in x-ray, R = 12.4-24.8 A, G = 9.3-12.4 A, B = 6.2-9.3 A.	source
	A jet from a young star in the Carina Nebula, R = 6730 A, G = 6560 A, B = 5020 A.	source
	A jet from a young star in the Carina Nebula in infrared, Orange = 16,400 A, Cyan = 12,600 A.	source
	M 51 in visible light.	source
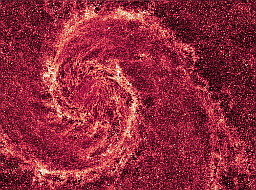	M 51 in infrared, with most of the visible light removed, showing the distribution of dust.	source
	The Large Magellanic Cloud in visible light (ESO).	source
	The Large Magellanic Cloud in infrared, Red = 2,500,000 A, Green = 1,000,000 and 1,600,000 A (Herschel), Blue - 240,000 and 700,000 A (Spitzer).	source

Near-Infrared observation allows us to "see through" cold dust to the warmer dust and stars inside.
Far-Infrared observation allows us to image cooler dust (as in the last LMC image).
Ultraviolet observation reveals hot, massive stars.
X-ray observations shows hot gases, as well as matter accreting onto neutron stars or black holes.
Radio observations reveal neutral Hydrogen atoms, both in the galaxy itself and in the surrounding halo.

We see that higher frequency or energy, and smaller wavelengths, correlate with higher temperature. This is natural, because temperature is simply a measure of thermal energy.

Almost all that we know about the universe comes from these five attributes of electromagnetic radiation:

the direction it comes from;
Pressure waves in the Sun, caused by violent events on the surface, can travel through the Solar interior. As they do so, they undergo refraction: their direction of propagation changes because the speed of sound changes with depth (the speed of sound depends on density and temperature, which increases with pressure). Astronomers have exploited these changes of direction to explore the details of the Solar interior; this is known as Helioseismology.
the intensity we receive (power, or energy per unit time, over area);
The total power output over all wavelengths is called the luminosity, and is related to the intensity by
intensity = luminosity / (4 π distance²)
This is often called the inverse square law, and is a result of the fact that in three spatial dimensions ("3D"), the area of a sphere is 4 π r²: the electromagnetic radiation propagates symmetrically in all directions, so surfaces of equal intensity are spheres:

The inverse square law.

So the luminosity is determined by the source, but the intensity also depends on where you are when you are looking at it.
the wavelength (or frequency);
the relative phase (see interferometry); and
the polarization (the direction of its electric field).
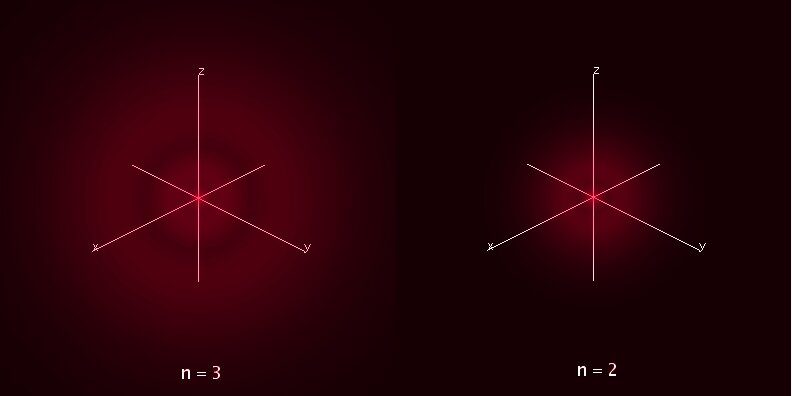
In general, electromagnetic waves are radiated such that their electric field directions are randomly distributed. If, however, they pass through a medium whose molecules have been oriented along a magnetic field, the medium can polarize the waves so that their electric fields are aligned along a single direction (this is the same principle used in polarized sunglasses, except there it is not a magnetic field but a crystalline structure that is responsible for the polarization). Astronomers have very cleverly used the amount of polarization to measure the magnetic fields of the interstellar medium. Most such measurements are in radio wavelengths, and typically give magnetic field strengths on the order of 10^-5 to 10^-4 that of the Earth, although fields near the galactic center have been measured to be of order 10 times stronger.

While electromagnetic wave direction, intensity, wavelength, phase and polarization account for the vast majority of our knowledge of the universe, there are three notable exceptions: cosmic rays, neutrinos and gravitational waves.

We often measure the spectrum of an object: the distribution of the intensity (energy per unit area per unit time) of the electromagnetic radiation we observe as a function of wavelength. We will return to this subject soon.

Interferometry

This applet illustrates how individual waves can reinforce and cancel each other out. Press the "Start" button, turn the blue and red waves "on", and choose the black and blue wave modes to be the same. Then vary the blue phase angle from 0 (reinforcement) to π (cancellation):

This reinforcement and cancellation varies with time and position to produce an interference pattern. This is the interference pattern produced by two sources (which are located at the bottom of the plot):

Alternatively, if we place two or more telescopes at different locations and look at the same object, we can use the information about how their images interfere to construct a more detailed picture of the object. The positions of the telescopes must be determined very precisely, so this technique is primarily practical for ground-based astronomy. Since the atmosphere is opaque to far ultraviolet and many infrared wavelengths (due to absorption by water, Oxygen and Carbon Dioxide), interferometry is limited to optical, radio and a few near-infrared ranges.

Please send comments or suggestions to the author.