
We would like to generalize our discussion of your fall from the roof to include the possibilities that you jumped off or were pushed. We do this not for morbid reasons but because this simple extension of the problem demonstrates an essential idea that we mentioned earlier: motion in perpendicular directions (such as x and y) are independent of each other.
When you simply fell from the edge of your roof, your initial velocity was zero. If you were to jump off of your roof, you would have a non-zero initial velocity in both the direction of your jump and the vertical direction relative to the ground. We will take the plane of your jump to be the x-y plane, with y(t) again denoting your vertical position (your height above the ground at any time t). x(t) will denote your position relative to the edge of your roof in the plane of your jump (your distance away from the house at any time t).
The following applet will graph your position in the x-y plane, given the initial conditions: the height from which you jumped, your initial velocity and the angle from the horizontal of your jump. Angles above the horizontal are positive, while angles below the horizontal are negative. The program will display your position and velocity as a function of time. It will also trace your vertical position in green on the y axis, and your horizontal position in light blue on the x axis. The program slows time down by a factor of 20 so that you can more carefully observe the jump.
There are several things to notice here. Perhaps the most obvious is that your horizontal velocity did not change. Because we are again ignoring air resistance, the only acceleration is due to gravity; therefore your horizontal velocity remains constant. The other thing to notice is that at the height of your jump, your vertical velocity was zero. This is an example of a situation in which you can have zero velocity but nonzero acceleration.
The equations of motion for the y direction are nearly the same as in the one dimensional case:
These equations are clearly independent of each other: that is, the x equations do not depend on y or vy and the y equations do not depend on x or vx. They both depend on t, which makes t a sort of parameter; it is the only truly independent variable in this set of equations.
One question remains: how does one compute vx0 and vy0 from v0 and θ0 (the Greek letter theta, denoting the angle of your jump)? Your initial velocity has both a magnitude and a direction which can be decomposed into x and y components:
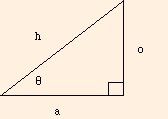
By using elementary right triangle trigonometry:
sin θ = 0 / h
cos θ = a / h
we see that we can express the x and y components of your initial velocity as
We can now extend our problems from the previous section to include questions about how long it took to reach your maximum height, what your maximum height was, and how far from the house you landed. We will assume that when you hit the ground, only the vertical component of your velocity at that point contributed to your injuries.
The next section is about dynamics: why it hurts when you fall.
©2003, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
It also changes the scales so that your trajectory always fills the plot area. This helps illustrate that every trajectory is a parabola, no matter how far
along the x axis you travel before you hit.
y(t) = y0 + vy0t - g t2 / 2
and
vy(t) = vy0 - g t.
Because the acceleration in the x direction is zero, the equations for it are
x(t) = x0 + vx0t
and
vx(t) = vx0.
We take the origin of the x axis to be at the edge of your roof, so that x0 is zero.
vx0 = v0 cos (θ0)
and
vy0 = v0 sin (θ0).
Here, v0 corresponds to h (the hypotenuse), while vx0 corresponds to a (the side adjacent to the angle θ0) and vy0 corresponds to o (the side opposite the angle θ0).