
Now that we have completely described your fall from the roof and subsequent collision with the ground, we are ready to ask two more sophisticated questions: why did you fall in the first place, and why did it hurt when you stopped?
It was Isaac Newton who first understood that objects only change their velocity under an external influence. An object at rest will remain at rest, and an object moving in a straight line will continue along that line with a constant speed. Changes in velocity can involve changes in speed but not direction, changes in direction but not speed or changes in both speed and direction. As we know, changes in velocity are proportional to acceleration, and so we say that an object can only experience acceleration under the influence of an external force.
As we will learn later, all objects experience a mutual gravitational attraction. This attractive force causes them to accelerate toward one another, which is why you fell in the first place. While gravity is always attractive, other forces may be repulsive: the objects experiencing the force move away from each other along the line connecting them. And since force has direction, an object may experience two equal forces in opposite directions which cancel, so that the object does not accelerate at all. But in all cases, a force is exerted between two objects, and the objects experience that force with the same magnitude, but in opposite directions.
If you only weighed as much as a feather, you would have fallen to the ground unruffled (even ignoring air resistance). Since your weight is considerably larger, your fall will leave you bruised or even broken. In fact, the weight of an object is actually the magnitude of the force of gravity acting on it. Since force is proportional to acceleration, and we know that the acceleration due to gravity is a constant near the earth's surface, there must be another factor in your weight versus that of the feather which makes the difference in the amount of damage you sustain. This factor we call mass, and force is equal to the product of mass and acceleration.
The mass of an object is a measure of its inertia, or resistance to acceleration: since force is proportional to both mass and acceleration, if the same force is experienced by two objects of different mass, the object with the smaller mass will experience the larger acceleration. It may have surprised you when we stated earlier that you fell because you and the Earth experienced a mutual attraction. If you were thinking, you realized that this means the Earth must accelerate as well! Now we have the resolution to this apparent paradox: both you and the Earth experience the same magnitude of attractive force, but the Earth's mass is so much greater than yours that its acceleration is negligible.
The mass used in the equation for weight is gravitational mass:
Mass is another of our fundamental variables, along with position and time. In S.I. units, it is measured in kilograms (denoted kg); at the surface of the earth, an object whose mass is 1 kg weighs about 2.2 pounds. As we shall see, the constant acceleration due to gravity (denoted g for gravity, not grams) depends both on your altitude and on the mass of the planet you happen to be on. So while the weight of an object depends upon its environment, the mass of an object is an intrinsic quality.
Since force is the product of acceleration and mass, its S.I. unit of measure is the kg m/s2. This is called a Newton (denoted N). Given your mass in kilograms, it is trivial to compute your weight in Newtons. For instance, a 1 pound object weighs about 4.5 N. What is much more interesting is to compute the force you experienced when you hit the ground. But we still lack the means to evaluate that force and determine the extent of your injuries.
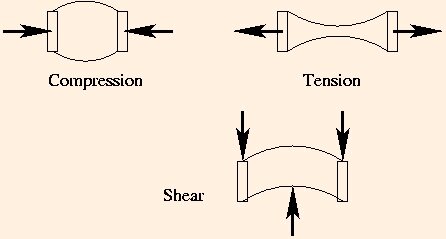
Let us first accept the fact that your fall will leave you bruised, and concentrate on the question: will you break a bone? As you know, bone is a rigid material but is not unbreakable. It can break under compression, as might occur in a direct impact. It can also break under tension, but stretching is not relevant in this case. Finally, it can break under shear stress, when forces are applied in different directions at different points.
Shear is a distinct possibility in a fall, but it is so difficult to handle mathematically that we will restrict ourselves to a discussion of breakage by compression.
Compressive strength varies from one type of bone to another, as well as from one specimen to another. It is measured as a pressure (denoted P): a force per unit area. The S.I. unit of pressure is the Pascal (denoted Pa), and is equivalent to one Newton per square meter (N/m2). Since a Newton is not a particularly large unit of force and a square meter is a large unit of area, measurements of pressure usually involve metric prefixes (we include small as well as large ones for the sake of completeness; you should already be familiar with most of these):
Typical values for some types of human bones are:
So we see that we need two additional pieces of information in order to find out how badly you were hurt: the compressive strength of the bone which took the impact (we will assume that a single bone took all of the impact), and the size of the area which hit the ground. Knowing the force and surface area of the impact, we can compute the pressure which was applied to the bone, and compare that to the strength of the bone to determine the extent of the damage.
The following applet builds from the one in the last section. Decide which bone took the impact and compare your answer for the pressure to the table above to decide if you are headed back up the ladder or to the hospital!
The next section discusses two fundamental conservation principles which lie at the very heart of physics.
©2003, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
W = m g.
When we speak of inertial mass, we mean the mass which determines how much acceleration you experience under the influence of a given force, as given by Newton's Law:
F = m a.
While there is no conceptual reason why these two masses should be numerically equal, they are. This is one of the fundamental mysteries of physics.
Elasticity and Strength
bone compressive strength (MPa) femur (upper leg) 167 humerus (upper arm) 132 radius (forearm) 114 tibia (shin) 159 cervical vertebrae (neck) 10 lumbar vertebrae (lower back) 5