
Within the confines of our point particle approximation, we have done rather well: given the height from which you jumped, your initial velocity, the time it took you to stop, your mass and the size of the impact area, we have been able to completely describe your fall and its consequences. If this has been your first exposure to physics, it has probably seemed to be a complicated analysis. Yet many if not most of the problems to which physics addresses itself are beyond any such complete treatment.
When trying to understand a complex physical process, the physicist looks for quantities which remain constant. Such a conserved quantity is often a signal that a conservation principle is at work, and that a more sophisticated understanding of the problem is possible. A number of conservation principles have been identified by physicists; two of the most important ones are the conservation of energy and the conservation of momentum.
For the purposes of the present discussion, we will divide energy into two types: kinetic and potential. Kinetic energy is the energy an object has by virtue of its motion; it is defined as
Potential energy is the energy an object has by virtue of its position in the presence of an external force. When you were on the roof attempting to clean the gutters you had a higher potential energy than when you were on the ground. Potential energy is always relative, so that it is necessary to fix a point at which it is zero before we can decide whether it is positive or negative at any given position. In the case of your gravitational potential energy in the presence of the Earth's gravitational attraction, we typically say that the potential energy is zero at ground level.
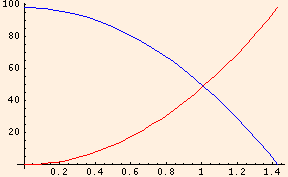
We are now ready to state the principle of conservation of energy: in the absence of dissipative forces, such as those involving friction or drag (air resistance), the sum of the potential and kinetic energies of an object is a constant. When you fell from rest, your potential energy steadily decreased with your distance from the ground:
= m g h - m g2 t2 / 2
= m g2 t2 / 2
Here we have plotted the kinetic energy in red and the potential energy in blue.
When you jumped, you had an initial kinetic energy equal to
= m v02 / 2 + m g2 t2 / 2 - m g vy0 t
= m g h + m g vy0 t - m g2 t2 / 2.
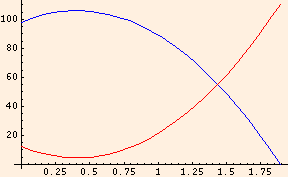
Note that the kinetic energy has a minimum precisely where the potential energy is a maximum, but that it is never zero. This corresponds to the vertical component of your velocity dropping to zero at the height of your jump, while the horizontal component of your velocity is constant throughout.
In your actual collision with the Earth, energy was not conserved. It was dissipated, both in the compression of the ground and the creation of your injuries. Energy is only conserved in collisions when they are perfectly elastic. This only happens in cartoons, although it is a decent approximation when the colliding objects are not deformed. When energy is expended (such as in your collision), we can define the rate at which it is expended as the power. Power is denoted by the letter P, as is pressure; you must distinguish between the two based on the context (this will happen again: there are not enough letters in the alphabet to avoid it!). The S.I. unit of power is the kg m2 / s3, otherwise known as the Watt (denoted W). This is the same Watt that you are familiar with in light bulbs, where the energy being expended is electrical.
Because energy is conserved during your fall, we say that gravity is a conservative force. One of the characteristics of a conservative force is that your energy depends only on where you are and not how you got there: you have the same energy at the edge of the roof if you climbed there directly from the ground or if you took a ride in a helicopter and were lowered there from the air. Dissipative forces are not conservative: when pushing a box against the force of friction, the amount of energy expended depends on the length of the path you take.
Note that in all of this discussion, energy is an attribute, much like mass, or even velocity or position. Energy is not a
substance, although many texts treat it as such. It is a concept of profound use in physics: physicists are always asking questions like
"what is the configuration of least energy?", or "where was the energy transported to?", in order to learn more about the behavior of a system.
Momentum (denoted by p!) is defined as the product of mass and velocity (with S.I. units of kg m / s). As such, it agrees with your intuitive definition of the term: objects with greater mass and velocity are harder to stop than smaller objects moving more slowly. In any closed system, such as a set of two colliding objects, the total momentum is conserved. Moreover, since velocity carries with it direction, momentum does as well. Hence in any given direction, the total momentum is conserved. For instance, consider the collision of two billiard balls on a pool table. If we fix the x axis along the length of the table and the y axis on its width, the sum of the momenta of the two balls along the x axis is the same before the collision as after; the same holds true for the momenta along the y axis.
Just before you hit the ground, your fall had given you a rather large momentum. After you came to rest, your momentum was now zero. But that momentum was not lost: it was transferred to the Earth, which now has a slight velocity along the direction of your fall. As in the case of your mutual gravitational attraction with the Earth, this velocity is negligible, because the mass of the Earth is much greater than yours.
Notice that an external force can change the momentum of an object. This should of course be obvious, since a force implies acceleration and acceleration implies a change in velocity.
You now have some work to do. The following applet is like the one you used to construct the equations of kinematics. You will use it to construct equations involving energy, momentum and power, which you will then use in the second applet below.
Note that the equation you just created for gravitational potential energy, when equated to the kinetic energy, yields one of the equations you created for kinematics! Conservation of energy was implicit in our kinematics treatment because we are ignoring dissipative forces. Also note that force can be expressed as a rate of change as well as a gradient: a change over position instead of over time. This is true for all conservative forces.
Now we will analyze your fall using the conservation principles and the equations you have just constructed. Note that we will be solving a
slightly different problem from the one we have been solving. In previous applets, we have been computing the vertical component of the
velocity you had when you hit the ground. But energy is a scalar: unlike vectors, it has no direction associated with it.
So when you use conservation of energy to find your velocity just before you hit, you are actually finding the length of the velocity
vector and not just the vertical component. In the past we assumed that the vertical component of your velocity was responsible for
any injuries you sustained; here we ask slightly different questions, ones more suited to the use of conservation principles.
In the next section we will apply what we have learned here to see why friction is so important to your everyday life.
©2003, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
Energy
K = m v2 / 2.
Since mass is always positive, we can see that the kinetic energy is also always positive. The S.I. units of energy are clearly kg m2 / s2, which are called Joules (denoted J). As is obvious, a one kg mass moving at one meter per second has one half Joule of kinetic energy.
U = m g y
Simultaneously, your kinetic energy steadily increased as you approached the ground:
= m g (h - g t2 / 2)
K = m v2 / 2
And since we are ignoring air resistance, the sum of the two was a constant (m g h) at every point along the path of your fall:
= m (-g t)2 / 2
K0 = m v02 / 2
(from the Pythagorean Theorem), and your kinetic and potential energies were
= m (vx02 + vy02) / 2
K = m v2 / 2
and
= m (vx02 + (vy0 - g t)2) / 2
U = m g y
Their sum is m v02 / 2 + m g h throughout your trajectory:
= m g (h + vy0 t - g t2 / 2)
Momentum