
Living things are so well constructed that friction plays little role in their function. Only in cases of disease, such as arthritis, do bones come into contact, and the friction between them causes many of the symptoms. Yet there is one activity undertaken by all land animals in which friction plays an important and necessary role: walking.
Consider a walking biped, here idealized as a point particle with legs:
The right leg has been drawn in red, the left in blue. There is a slight pause at the end of each stride, which will simplify our analysis by allowing us to model walking as a series of independent steps. In real life, there is a cyclic variation in forward speed, but the animal obviously does not come to a complete stop before each new stride.
Just at the end of a step, the animal has a linear momentum of
p = m vin the horizontal direction. If the animal is not to slip, the moving foot must stop in a relatively short time t. This means that the animal experiences a force of
Fstop = m v / tand therefore an acceleration
a = v / tin the opposite direction. This force is provided by friction.
The force of friction is empirically found to be proportional to the weight of the object upon which the friction acts. If friction prevents the object from moving, as in this case, the constant of proportionality is called the coefficient of static friction and is designated μs (using the Greek letter mu). If the object is moving but slowed down by friction, the constant has a smaller value and is called the coefficient of kinetic friction and is designated μk.
The coefficients of friction depend on the types of surfaces that are in contact; typical values of interest to shoe-wearing animals are:
At the end of one step:
μs rubber on dry concrete .5 to 1.2 rubber on wet concrete .45 to .8 rubber on dry asphalt .35 to 1.2 rubber on wet asphalt .25 to .8 rubber on dry gravel .4 to .85 rubber on wet gravel .4 to .8 rubber on dry rock .55 to .75 rubber on wet rock .55 to .75 rubber on dry ice .07 to .25 rubber on wet ice .05 to .1 rubber on dry snow .1 to .55 rubber on wet snow .3 to .6 (adapted from Baker, J.S., "Traffic Accident Investigation Manual", 1975)
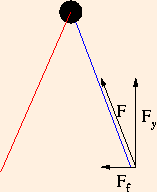
the animal's weight is distributed on both feet, so
Fy = m g / 2,and the force due to friction is
Ff = μs m g / 2.If the animal is walking down hill, the component of its weight which is normal (perpendicular) to the hill contributes to friction, but the component parallel to the hill acts against friction and contributes to slippage:
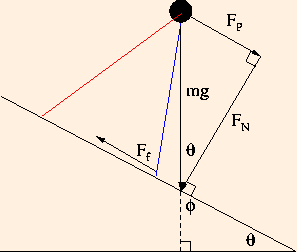
Here, the angle θ is complementary to the angle φ (they add up to 90 degrees), which gives us the forces
FN = m g cos (θ) / 2and
FP = m g sin (θ) / 2.This means that the force
Fstop = Ff - FPis available to prevent the animal's foot from slipping.= μs FN - FP= μs m g cos (θ) / 2 - m g sin (θ) / 2
If the animal is walking up hill, the component parallel to the hill acts with friction, so that
Fstop = Ff + FPand a smaller coefficient of friction is required to walk safely.= μs m g cos (θ) / 2 + m g sin (θ) / 2
By equating the force available to stop to the force necessary to stop at the end of each step, and given the coefficient of friction and your speed, you can determine how long it will take you to stop each footfall, and therefore how carefully you must walk in order to avoid slipping.
In the next section, we will see how everything you have learned about linear motion has an analog in rotational motion.
©2006, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.