
The analysis of linear motion which we have just completed has application in the movement of every organism in the animal kingdom. By contrast, there seems to be little use for rotation: very few animals revolve. But every animal with articulated joints participates in some measure in rotational motion: the movement of one bone relative to another to which it is joined is a partial rotation about the axis located at the joint. Whenever you walk, swing your arms, throw a ball or turn your head, you are moving rotationally.
Uniform Circular Motion
Consider a pitcher throwing a ball in a game of fast pitch softball. We choose this example because the motion of the ball around the joint at the shoulder is very nearly circular, at least until the ball is released. As you can imagine, circular motion is the most simple kind of rotational motion: it is the rotational analog of one-dimensional linear motion. In keeping with our use of the point particle approximation, we will model the windup before the pitch as the circular motion at constant speed of a point object (the ball) about a fixed axis (the shoulder joint) in a plane.
Let us first examine the kinematics of the motion. While the ball is assumed to be moving at constant speed, it is most certainly not moving with constant velocity since the direction of the ball's motion is constantly changing as it moves around the circle. In this example, there are only two degrees of freedom: the radius of the circle and the speed of the ball. The centripetal acceleration experienced by the ball is a function of these two variables, and keeps the ball in a circular path.
When the ball is released it moves along a straight line tangent to the circle at the point of release. In fact, at any point along the circular motion, the direction of the velocity is tangent to the circle. This means that the direction of the centripetal acceleration is inward, toward the center of the circle. The centripetal force causing this acceleration must then be an attractive tension connecting the ball and the shoulder joint: it constrains the ball to move in a circle. Because the arm is a radius of the circle, we say that both the acceleration and the force are radial.
If we substitute these expressions into our general formula for position, and then divide by the constant factor of the radius, we have an expression for the angle as a function of time:
Perform the following experiment right now, while you are reading this text. Stand holding your loaded book bag by its straps loosely at your side. Keeping your arm stiff, slowly raise your book bag to shoulder level, if you can. Now loop the straps around your arm at the elbow joint and slowly raise the book bag to the same height. It is almost painfully obvious that less effort was required to lift the bag when it was closer to your shoulder. It is equally obvious that less effort is required when the bag is less full. Generalizing, we see that the rotational inertia of an object depends not only on its mass but also on the radius of its rotational motion. In this context, the radius is often called the lever arm.
Consider the force involved in this experiment. Since this experiment took place in two dimensions (as circular motion), the force may have any direction in the x-y plane. Taking the lever arm to extend along the x axis from the origin, we see that an arbitrary force may have independent x and y components. These are identified by drawing a right triangle whose hypotenuse is the force, and whose other sides are parallel to the x and y axes. The y component is labeled here as FN: the component normal to the lever arm. The x component is labeled as FC: the component parallel to the lever arm might act to compress it, but will not affect the rotation:
At both values of the lever arm, the book bag had the same mass and experiences the same acceleration. Hence the force was the same in both cases; yet the effort was considerably different. In order to quantify the effort we define the torque (denoted by the Greek letter tau) as the product of the length of the lever arm and the force acting normal to the lever arm:
The rotational dynamics equation isomorphic to the linear equation F = m a should be
We are now in a position to construct equations for the variables of rotational motion which are isomorphic to their linear counterparts:
Several of the equations which you have constructed involve angular momentum. Just as momentum is always conserved in collisions, angular momentum is conserved when, for instance, there is a change in rotational inertia. The classic example of this is the spinning ice skaters who move their arms from an outstretched position inward to their bodies: their rotational inertia becomes smaller causing their angular velocity to increase. In fact, the conservation of momentum and the conservation of angular momentum seem to be universal phenomena.
You have also constructed an equation for rotational kinetic energy; in general, a complex object may rotate as it translates (moves linearly), and so its total kinetic energy is the sum of its rotational and translational kinetic energies. In the absence of dissipative forces, that sum is conserved. Note that since our fast pitch softball problem is one dimensional, the ball has only rotational kinetic energy before it is released. That energy becomes translational kinetic energy upon its release.
We are now ready to get some quantitative practice with rotational motion. But first, we must be careful with our measurement of angles. While angles have no units, it is customary to measure them in degrees, with 360 degrees in a circle. This custom is inconsistent with our relationship between arc length and radius: the arc length of a complete circle is 2π times the radius. Therefore our measurements of angle must yield 2π for a complete revolution. For this reason we measure angles in radians, where 90 degrees is equivalent to π/2 radians, etc.
As we discussed above, we are using the point particle approximation to describe the pitch of a softball. Hence we will give the length of your arm and a combined mass, which will include the mass of your arm as well as the mass of the ball. Note that in this case, angular velocity is NOT a constant!
What is the relationship between centripetal force and centrifugal force? Centrifugal force is not a real force.
It is an apparent change in velocity which occurs inside
a rotating object (or as physicists would say, a rotating "frame of reference"), opposite to the direction of rotation.
Physicists call it a "pseudo-force".
Consider a car following a sharp turn to the left at speed. During the turn, the car is in circular motion: it follows an arc
on a circle. At every point along that arc, its velocity vector is tangent to the arc. So, too, are the velocity vectors
of everything in the car: an object dropped from the car during the turn would move in a straight line along the tangent at that point on the arc:
The moving car constrains you to follow the arc, and the "force" you feel which seems to push you to the right is nothing more than your
tendency to follow the tangent. From the point of view of an external observer, the only force you experience points toward the
center of the arc: it is the centripetal force, here exerted by the friction between the tires and the road surface, which
keeps the car moving along the arc.
There is another pseudo-force whose results you have seen: Coriolis force. Consider a huge, violent low-pressure weather system:
a hurricane. If the Earth did not rotate, all the wind would blow radially into the center of low pressure. Now
the tangential velocity at the Equator is over 1000 miles per hour, but as you move away from the Equator it diminishes
(circles of constant latitude grow smaller with increasing latitude). Hence in the northern hemisphere, air blowing south
lags behind the faster rotating surface and so appears to be deflected to the west of the low pressure area. Meanwhile,
air blowing north gains on the slower rotating surface and so appears to be deflected east of the low.
This means the air will rotate counterclockwise around the low pressure center. In the southern hemisphere the opposite happens,
with the result that the air rotates clockwise.
Contrary to what you have probably learned, this is not what determines the direction of rotation of a draining bathtub
or sink. The Coriolis force is far too weak to act noticeably on such small vortices. The direction of drain rotation depends on how
the motion gets started as well as on the shape of the draining vessel. For more see the
Bad Coriolis web page.
In the next section we will use the tools of rotational motion to analyze your body in equilibrium: when forces are present but nothing moves.
©2008, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
General Rotational Motion
Let us now consider a small arc of the circle, and relax the condition that the ball be moving at a constant speed. Since the radius of the arc is a constant, there is a direct geometric relationship between the length of the arc and the angle subtended by it. Denoting this angle, or more properly, angular position, by θ, we have
x = r θ.
Because the radius is constant, we also have a simple relationship between the velocity of the ball and the rate of change of the angle, called the angular velocity and denoted by the Greek letter omega:
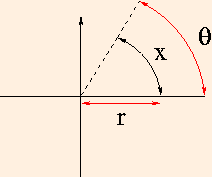
v = r ω.
Similarly, the relationship between the acceleration of the ball and the angular acceleration is
a = r α,
where α is the Greek letter alpha. Since angle is the ratio of arc length to radius, angles carry no units. Hence the S.I. units of ω are 1/s and those of α are 1/s2. As in the linear case, we will assume that angular acceleration is always constant.
θ = θ0 + ω0 t + αt2 / 2.
Since this equation looks exactly like the position equation with a simple substitution of variables, we say that these two equations are isomorphic: they have the same shape. In fact, the equations of rotational motion are all isomorphic to their linear counterparts. This isomorphism is possible because linear motion and rotational motion around a circle are both one-dimensional: angular position is just as good a variable as linear position.
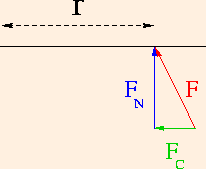
τ = r FN.
τ = I α,
where I denotes the rotational (moment of) inertia. But we have just seen that torque has S.I. units of Newton meters, or kg m2/s2.
Note that while at the fundamental level these are units of energy, torque is not energy.
This implies that I has units of kg m2; since we know that rotational inertia depends on both mass and radius, we must have
I = m r2
for a point particle rotating around a circle. For more complex objects we need calculus in order to split the objects into infinitesimal pieces and add together the rotational inertia of all of the pieces.
