
Consider a one dimensional game of tug of war: each team is constrained to pull along the x axis. If the teams are evenly matched, the force exerted by the team pulling in the positive x direction will be equal in magnitude to the force exerted by the team pulling in the opposite direction. Since the forces have equal magnitude but opposite direction, their sum is zero. Whenever the sum of the forces experienced by an object are equal to zero, it is said to be in equilibrium. An object in equilibrium which is also at rest is said to be in static equilibrium: its velocity and acceleration are both zero.
Let us now broaden our horizons by considering a three-way tug of war constrained to the x-y plane. The force exerted by each team can have both an x component and a y component:
The dot in the center of this picture represents the system of the three opposing teams in the point particle approximation. It is the location of the center of mass (also called the center of gravity) of the system. Any system of objects can be broken down into tiny pieces, each with its own mass mi (where i indicates the identity of each piece) and its own x and y coordinates xi and yi. The center of mass of the system is defined to be the point which, if taken to be the origin, results in the sum of the products mixi being zero, and the sum of the products miyi being zero. Hence it is a sort of mass-weighted central position.
The sum of the forces in the x direction will be zero if the sum of the magnitudes of the forces pulling left are equal to the sum of the magnitudes of the forces pulling right:
ΣFup = ΣFdown.
Consider a one-dimensional object lying in a plane with forces acting on it has shown:
Since there are no forces acting in the y direction, and the sum of the forces acting in the x direction are zero, the center of mass of the object will not move. It is clear however, that the object will rotate about its own center: the torques due to both forces result in rotation in the counterclockwise direction. So we see that in two dimensions, there are actually three conditions for equilibrium:
ΣFup = ΣFdown and
Σ τcounterclockwise = Σ τclockwise.
We will illustrate the use of these conditions with several examples from the human body. In each case, notice that the idea is to keep the relevent body part from moving in either the horizontal or vertical directions, and, once a convenient pivot (axis of rotation) is chosen, to keep the part from rotating around that pivot.
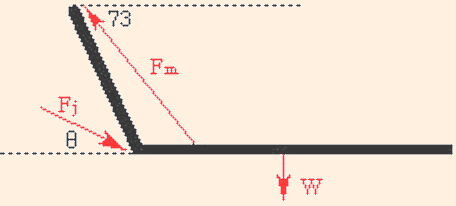
Consider the following idealized arm:
We wish to find the forces required to hold the arm in place. The biceps muscle pulls upward with a
tension (force) Fm, and the upper arm exerts a force Fj at the elbow joint, on the lower arm to keep it in place. For the purposes of this example, we will assume that the biceps muscle is attached to the arm 4 cm from the elbow, and that the lower arm is 40 cm long. The mass of the lower arm is assumed to be 14 kg; this causes a force W which is exerted downward by gravity at its center of mass. This is at its midpoint, since it is assumed to be a uniform rod.
Our first step is to identify the x and y components of each force:
Note that we do not need to do this for W; it is already vertical, and has no horizontal component. Using standard right triangle trigonometry, the x and y equations are:
and
where W = m g.
The next step is to choose a pivot for the torque equations, and identify the force components which are perpendicular to the lever arm. For this system the lower arm is the lever arm, and we choose the elbow for the pivot. Since Fj acts at the pivot, its lever arm (distance from the pivot) is zero, and hence so is its torque. The components of the forces which are perpendicular to the lever arm are Fmy and W, since in this example the lever arm is horizontal. Since the lever arm for the bicep is 4 cm and the lever arm for the weight W is halfway up the 40 cm arm, the torque equation is:
From it we obtain Fm = 717 N. Note that in the torque equation, we don't have to convert the lever arm lengths to meters; it is only necessary that the units match on both sides. Subtracting W from both sides of the y equation and dividing it by the equation for x, we obtain
This gives us a value of 69 degrees for θ, and 587 N for Fj.
Now consider the compression of the vertabrae in the spine which occurs when a person leans over:
For this example, we will assume that the muscle is attached two thirds of the way up from the bottom of the spine; the mass of the head and arms is 16 kg, and the mass of the torso is 32 kg. Note that in this case, the weight of the torso is applied at the center of mass, and the head is treated as a point mass at the end of the torso. Our first step is to identify the x and y components of the forces:
Here we have exaggerated the forces in order to clarify the drawing. The x and y equations for this problem are:
and
The next step is to find the components of the forces which are perpendicular to the lever arm. The lever arm is the spine, and the pivot is chosen at the base of the spine to eliminate Fj from the torque equation. We now draw triangles (again exaggerating the forces) whose hypotenuse are the forces and whose sides are perpendicular and parallel to the lever arm:
At this point we don't know the angle x, but we do know that the triangles with the vertical weights are similar. Consider the following triangles:
Since the sum of the angles in a triangle is 180 degrees, and these are right triangles, we know that
and
This implies that x = 30 degrees. Since the muscle acts two thirds of the way up the spine, that is its lever arm; the lever arm for the weight of the torso is at its center of mass in the middle of the spine, and that for the head is at the neck end of the spine. The torque equation is then
where L is the length of the spine. Note that since it appears as a factor in every term in the equation for torque, the length of the spine is not important in this problem. Note also that the angle in the torque equation is different from that in the x and y equations. This is because the torque is computed from the component of the force which is perpendicular to the lever arm, which is this example is not the y component! The solution for this problem is
Fj = 2151 N and
θ = 30 degrees.
Fj = 2800 N and
θ = 29.1 degrees.
We have presented two examples here because this material is often very difficult for students attempting it for the first time. Now it's your turn!
What is the relationship between equilibrium in physics and chemical equilibrium?
Chemical equilibrium is a dynamic process which has reached a steady state: some number (depending on temperature) of the reactants
are still turning into products, but some of the products are also turning back into reactants so that the equilibrium concentrations of each
are constant. Physicists often call this sort of equilibrium detailed balance, and it occurs frequently in statistical mechanics,
when we are dealing with large numbers of objects (like molecules).
The kind of equilibrium described in this section is often called
"statics", because all forces cancel and nothing can undergo a change in velocity; so if all velocities start out at zero, they
remain there. The skeletomuscular problems we examine are statics problems from a physical point of view, even though
the muscles are continually burning calories to maintain the static configuration. So from a biochemical point of view, the
system is not in equilibrium, while from a physical point of view it is.
The next section begins our work with thermal physics.
©2012, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
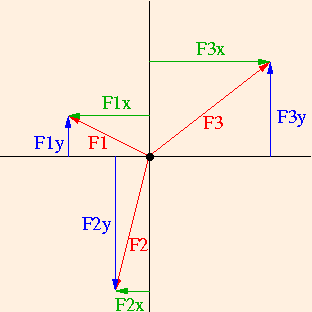
F1x + F2x = F3x.
Similarly, the sum of the forces in the y direction will be zero if the sum of the magnitudes of the forces pulling up are equal to the sum of the magnitudes of the forces pulling down:
F1y + F3y = F2y.
Using the capital Greek letter sigma to denote summation, we have
ΣFleft = ΣFright and
If these conditions are met, the center of mass of this system will not accelerate in either the x or y directions. But what about rotation?
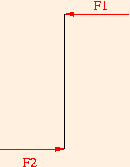
ΣFleft = ΣFright,
The first two conditions provide for translational equilibrium: the center of mass of the system will not move either left or right or up or down, and the final condition provides for rotational equilibrium: the system will not rotate about its own center of mass.
Skeletomuscular Equilibrium
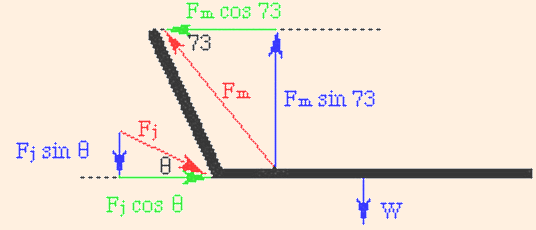
Fm cos 73 = Fj cos θ
Fm sin 73 = W + Fj sin θ,
4 Fm sin 73 = (40 / 2) W.
tan θ = (Fm sin 73 - W) / Fm cos 73.
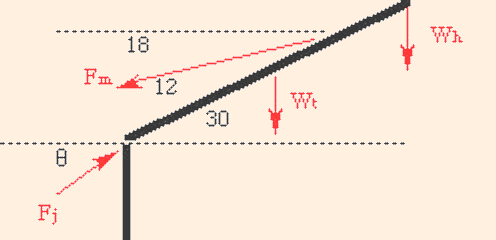
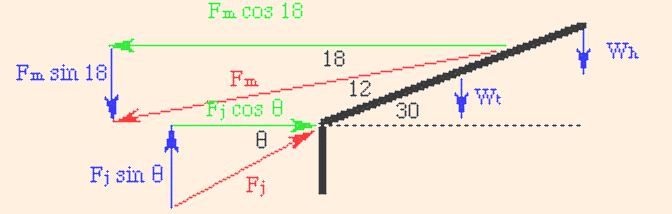
Fm cos 18 = Fj cos θ
Fj sin θ = Wh + Wt + Fm sin 18.
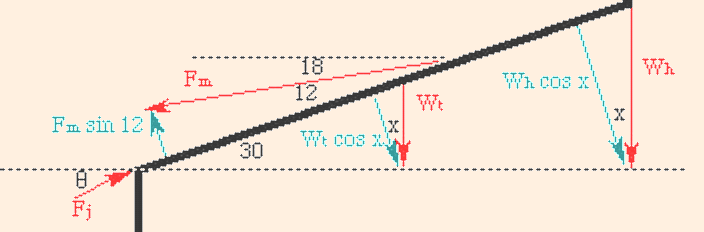
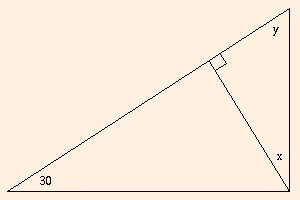
y + 30 = 90
x + y = 90.
(2 L / 3) Fm sin 12 = L Wh cos 30 + (L / 2) Wt cos 30,
Fm = 1959 N,
If the person is picking up a 10 kg mass, Wh is increased by 980 N and the new results are
Fm = 2572 N,
Compare this result with that from the previous example (particularly the values of Fj), and you will understand why lower back pain is such a common malady!