
Heat (denoted by Q) is thermal energy: the energy of a system of particles randomly colliding with each other and objects in their environment. It has dimensions of energy, but it is NOT a state variable: unlike temperature, its value does depend on the past history of the system. For instance, a system can be isothermally expanded by adding heat, or its pressure can be slowly decreased without the addition of heat. Yet the final pressure, temperature and volume are the same.
The temperature of a substance changes as heat energy is added to it. The heat capacity (denoted by C) of an object is the ratio of change in heat to change in temperature, and the specific heat (denoted by c) of a substance is the heat capacity per unit mass. We therefore have
latent heat of vaporization Lv, in the case of heat gained while changing from liquid to vapor.
The horizontal portions of the graph represent the phase changes. Note that the horizontal scale is measured in calories; 1 calorie = 4.186 J.
Since you are a warm-blooded animal, your body attempts to keep its internal temperature constant. Human life is only compatible with a narrow range of temperatures:
(adapted from ch. 53, table 2 of Physiology and Biophysics, T. C. Ruch and H. D. Patton, Saunders 1965)
Conduction is the flow of heat energy from regions of warmer temperature to regions of cooler temperature. As we can see from the following equation for the thermal current, or rate of heat flow:
Heat Flow
ΔQ = m c ΔT.
Some useful specific heats are:
Ice and water vapor (steam) are alternate phases of water. For a given substance at a given pressure, phase changes occur at well-defined temperatures. For water at standard atmospheric pressure (at the surface of the earth), those are 273.15K and 373.15K: 0 C and 100C, the freezing and boiling points, which define the Celsius degree, and therefore the Kelvin. For a given substance, the heat change per unit mass required for a phase transition is called the
water 4.186 kJ / kg K ice 2.135 water vapor 2.009 human tissue 3.558 air .963
latent heat of fusion Lf, in the case of heat lost while changing from a liquid to a solid, or the
This means that
ΔQ = m L.
The latent heat of fusion of water is 335 kJ / kg, and the latent heat of vaporization of water is 2260 kJ / kg at 100 C. Note that the heat added or lost during a phase change does not affect the temperature during the phase change. Icewater is at 0 C until all of the water has frozen; when melting, it is at 0 C until all of the ice has melted. Likewise, water is at 100 C until all the water has boiled away; if the water / steam system is in a closed environment, the steam is at 100 C until the water has all evaporated. Hence we can graph the temperature vs heat of a substance:
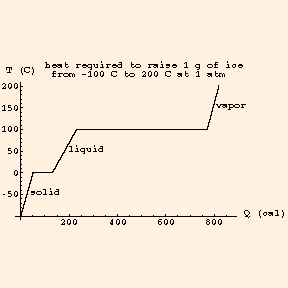
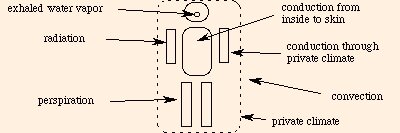
Body Temperature Regulation
Your body is constantly generating heat, and so it must take active steps to lose that heat. The following table illustrates the power cost of various common activities. The units indicate that the cost depends on an area: the surface area of your body. This is due to the fact that metabolic processes scale with area rather than mass or volume. This in turn is because your metabolism functions by maintaining concentration gradients across cell membranes, which are inherently two dimensional structures.
Temperature (C) Symptoms 28 muscle failure 30 loss of body temp. control 33 loss of consciousness 37 normal 42 central nervous system breakdown 44 death by irreversible protein damage
Approximately 80 % of the energy used by your body ends up as waste heat. The other side of this coin occurs during cold weather: your body must then work to stay warm. The mechanisms which either are used by your body or affect its function are conduction, convection, radiation and evaporation.
Activity Energy Cost (kJ / m2 hr) sleeping 150 sitting 210 working at a desk 250 standing 350 washing or dressing 420 walking (3 mph) 590 bicycling 1050 swimming 1465 running 2510
ΔQ / Δt = k A ΔT / Δx,
conduction is analogous to diffusion. The thermal conductivity k corresponds to the diffusion constant, and the temperature gradient (ΔT/Δx) corresponds to the concentration gradient.
We will define ΔT as the difference between your skin temperature and the ambient temperature, so all of our thermal currents will be positive when you are losing heat.
Note that Δx / k A is the common R-value of insulation. When multiple layers of insulating material are used (ie., in clothing), the total resistance to heat flow is just the sum of the individual resistances. Some useful conductivities are given in the following table:
We write the units here in a redundant form in order to emphasize the fact that thermal conduction is a function of both a surface area and a gradient.
substance conductivity in W m / m2 K air (0 C) .024 He / O2 mixture for diving .138 H2 O (20 C) .59 Cu 414 human tissue .21 fur or down .0042
Assume that you walk at 2.2 mph on flat ground. At this speed, an average person burns 14 kJ / min, 80% of which (about 187 W) must be lost in heat . Consider first the conduction of heat from the center of your body to the skin. Assuming that the average area (inside the body) through which heat is conducted is 1 square meter and that the average distance the heat must travel is 10 cm, the temperature difference necessary to maintain normal body temperture is 89 K! Clearly your body cannot rely on conduction for this service.
Now consider the conduction of heat away from the skin. Due to the nature of the surface of your body when immersed in air, it has a private climate about 3 mm deep through which the temperature changes from skin temperature to the surrounding air temperature. At room temperature (20 C), a person with 2 square meters of body surface area must (when nude) have a skin temperature of almost 32 C to lose this much heat when the air is still.
Convection is the movement of heat by currents in the medium, ie., the wind. The convection current in Watts is
Still air actually has a convection velocity of .23 m / s (called natural convection) because warm air rises. Within the private climate, this convection is in parallel with private climate conduction. For a 12 degree temperature difference, a person with a surface area of 2 m2 will lose about 167 W this way. Breeze convection usually provides much greater thermal current than private climate conduction. But we still have to get the excess heat to the surface.
Within the body, blood convection is used to move the heat from the inside of your body to your skin. Here the area is the surface area of the capillary bed, which for the average adult male is about 160 square meters. Using the skin temperature and heat current above, we see that the blood flow through the capillaries must be around .3 mm / s in order to move the excess heat from the 37 C interior to the surface. Since the specific heat of blood is larger than that of air, we expect the convection coefficient to be larger for blood; this coupled with the fact that capillary velocities are somewhat larger than this means that internal convection through the circulatory system is usually sufficient to keep the temperature essentially constant throughout the interior of the body.
Radiation is the emission of heat energy; it can occur even in a vacuum. The radiation current (in Watts) is
In all of the above mechanisms, when Ta > Tb the thermal current is negative, indicating that the body is absorbing heat from
its surroundings. But in the case of radiation in open air, there is another source of heat absorption by the body: solar radiation. On average, the
intensity of solar radiation at the top of the atmosphere is 1365 W/m2. The atmosphere blocks perhaps half of this (mostly in the
infrared and ultraviolet, and if you
use sun screen you will block more), and weather conditions can further attenuate the intensity, but the sun can make significant
contributions to the thermal current.
Evaporation is of course simply the change of phase of sweat. The rate of sweat is then related to the thermal current by the latent heat of vaporization:
Your body has a number of mechanisms to help it cope with cold weather. Constriction of surface capillaries is helpful when the ambient temperature is above 19 C (for a nude person). Shivering raises the average person's metabolic rate about 290 W / m2 (relative of course to body surface area). In fact, for any well-insulated animal, evaporative losses in breathing limits the ability to withstand cold temperatures.
We can summarize the various modes of heat transfer with the following diagram:
In this applet, you will be given the exposed surface area and temperature of a human body, the ambient temperature, conductivity and wind velocity, and the rate of water loss through sweat and exhalation. From these you will compute the total thermal current as the body maintains its internal temperature. Use the private climate depth for conduction currents.
For the final question, assume that both loss of consciousness and failure of the central nervous system are mortal dangers.
It is important to realize that
our computations for convection in water are incorrect: the factor of 14.5 in the convection equation is an empirical fit to data from
experiments in air. We lack sufficient data to obtain the correct coefficient in water, but we might imagine that the correct value is
closer to 63: the coefficient in air times the ratio of the specific heats of water and air.
Another empirical equation which you may find of some use is this expression for the surface area of a human body:
(from ch. 53 of Physiology and Biophysics, T. C. Ruch and H. D. Patton, Saunders 1965)
The next section applies the concepts of energy and entropy to help us understand many biochemical processes.
©2013, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
ΔQ / Δt = 14.5 A v1/2 ΔT.
when A is measured in m2 and v is the (wind) speed in m / s. This equation is an empirical equation: it is a fit to experimental data. Hence the units of the coefficient reflect the units that the measurements were made in: in this case, 14.5 W / m2 (m / s)1/2 K.
ΔQ / Δt = ε σ A (Tb4 - Ta4),
where ε is the emissivity, a dimensionless radiation "effectiveness", which is of order 1 for human skin. σ is the Stefan-Boltzmann constant (5.67 * 10- 8 W / m2 K4). The temperature must be in K due to the fourth power dependence; "b" denotes body, while "a" denotes ambient, or air, temperature. With the skin and ambient temperatures in the above scenario, your body's radiation power output is about 146 W.
ΔQ / Δt = (Δm / Δt) Lv.
At body temperature, the latent heat of vaporization of water is 2428 kJ / kg. For short periods, you can sweat up to 4 liters per hour; for longer periods (up to 6 hours), 1 liter per hour is common. In addition to sweat, however, your body also loses water vapor during respiration. The volume of air which you inhale with each breath must be humidified by your body to saturation in order to be used efficiently. This vapor is then exhaled, resulting in an evaporative loss which at high altitudes can rival sweat as a cooling factor. This makes evaporation a major contributor to heat regulation, up to a point: body functions are severely limited when you have lost 10% of your weight due to dehydration.
 . . .
. . .
A = 0.202 m0.425 h0.725.
Here m is mass in kg and h is height in m. A great many medical students underwent some degree of discomfort in the early
part of the 20th century to bring you this formula!