Curvature Invariants

Our motivation for studying curvature invariants lies in the inherent complexity of Riemann Geometry. We begin by discussing a number of metrics which illustrate some of that complexity.

We will define a diffeomorphism as a coordinate transformation which is differentiable to all orders and whose inverse exists and is likewise differentiable to all orders. This "passive" viewpoint is most convenient when doing computations on computers, and underscores the notion that diffeomorphism invariance in a physical theory such as General Relativity is equivalent to saying that physics should not depend on the coordinate system we use to describe it. The "active" viewpoint is of a smooth and invertible deformation of one manifold into another with the same topology.

Minkowski Spacetime (M⁴) is covered completely by the Cartesian coordinate chart

-infinity < x < infinity
-infinity < y < infinity
-infinity < z < infinity
-infinity < t < infinity.

The corresponding metric is of course

ds² = dx² + dy² + dz² - dt²

if we choose the positive signature.

A transformation to polar coordinates

x = ρ cos (φ)
y = ρ sin (φ)

gives us the metric

ds² = dρ² + ρ² dφ² + dz² - dt².

The (certainly not unique) inverse transformation is

ρ = (x² + y²)^1/2
φ = cos^-1 (x / ρ) for y > 0, or y = 0 and x != 0, and
φ = 2π - cos^-1 (x / ρ) for y < 0,

with

0 < ρ < infinity
0 <= φ < 2 π.

(We take the range of cos^-1 to be [0,π].)

This is actually a pair of diffeomorphisms, each covering one half of the x-y plane for any value of z (and t), excluding the origin. The two match on their boundaries (have the same value and derivatives there), and so we treat them as a single transformation.

But because the inverse transformation is not defined on the z axis. this diffeomorphism does not cover the region ρ = 0. There, all values of φ map to the same values of x and y. The metric is degenerate on the z axis, and of course, the inverse metric is singular there. We will call this a degeneracy singularity. For the polar coordinate chart, the z axis exists at ρ = 0, but there is no diffeomorphism between polar and Cartesian coordinates which includes it. From the "active" point of view, this diffeomorphism is a map between two manifolds which have the topology R⁴ - R.

Now consider a transformation from Cartesian to spherical coordinates:

x = r sin (θ) cos (φ)
y = r sin (θ) sin (φ)
z = r cos (θ).

This gives us the metric

ds² = dr² + r² dθ² + r² sin² (θ) dφ² - dt²

with degeneracy singularities at r = 0, as well as at θ = 0 and π. The inverse transformation for φ (not surprisingly) is the same as before, with the same consequences. Those for r and θ are

r = (x² + y² + z²)^1/2
θ = cos^-1 (z / r),

with

0 < r < infinity
0 < θ < π
0 <= φ < 2 π.

Again, the spherical chart covers the z axis (for values of θ equal to 0 and π), but there is no diffeomorphism between spherical and Cartesian coordinates which includes it.

The Schwarzschild Spacetime

The Schwarzschild Spacetime is the unique stationary spherically symmetric vacuum solution to Einstein's Equations. Associated with it is a conserved quantity we call mass, with the assumption that a spherically symmetric mass distribution centered on the origin is the source of the spacetime curvature. That assumption implies that there is a spherically symmetric "interior" solution with nonzero stress-energy which matches onto the Schwarzschild Spacetime. Hence the Schwarzschild Spacetime is expected to describe a region which is topologically R⁴ - B⁴, where B⁴ is a solid spatial ball extending in time.

If we have learned from our discussions of polar and spherical coordinates in flat space, we expect to be wary of the coordinates we use to describe the Schwarzschild Spacetime. Since it is asymptotically flat and spherically symmetric, we will use coordinates which asymptotically are the same as spherical coordinates in flat space. In these coordinates, the metric for the Schwarzschild Spacetime is:

ds² = r / (r - 2M) dr² + r² dθ² + r² sin² (θ) dφ² + (2M / r - 1) dt².

This metric is clearly singular at r = 0 and at r = 2M. In agreement with our topological expectations for this metric, r = 2M is the "edge" of a ball. Hence the asymptotically spherical coordinates are NOT the same as our flat space spherical coordinates: they only cover a submanifold of R⁴. But naively we might ask if the ball r < 2M is the one we should associate with the interior solution, or is there a different coordinate chart which extends the vacuum region there?

The Kruskal Coordinates for the Schwarzschild Spacetime are generally described implicitly as

(r / 2M - 1) e^{r / 2M} = X² - T²
t / 2M = 2 tanh^-1 (T / X).

Note that tanh^-1 (z) is only defined for | z | < 1, implying that | T | < | X |. With some help from Mathematica, we can find a slightly less implicit version:

Simplify[ Solve[ {(r / (2M) - 1) E^(r / (2M)) == X^2 - T^2, t / (2M) == 2 ArcTanh[T / X]}, {r, t}]]
{{t -> 4 M ArcTanh[T / X], r -> 2 M (1 + ProductLog[(-T² + X²) / E])}}

where ProductLog[x] is the solution for y in x = y e^y. Note that the domain of the ProductLog function is from -1/e to infinity, which maps into the range {-1, infinity}. This implies that there are values of X and T which correspond to r >= 0 as long as X² - T² >= -1.

Using the same technique to solve for X and T, we find that the inverse transformation is

X = e^{r / 4M} cosh (t / 4M) (r / 2M - 1)^1/2
T = e^{r / 4M} sinh (t / 4M) (r / 2M - 1)^1/2.

An equivalent transformation occurs if X -> -X and T -> -T.

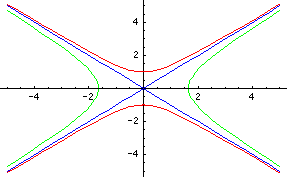
This diffeomorphism is defined throughout the region r > 2M. As we noted above, the continuation of this transformation to values of r < 2M corresponds to values of X² - T² > -1. This tells us that the Kruskal Coordinate Chart covers the region between the red lines in the X-T plane below, which includes the region covered by the original coordinate chart:

Because of the restriction -X < T < X, the diffeomorphism only covers the region between the blue lines T = +- X. These lines represent r = 2M for infinite t, which indicates that the t coordinate is also problematic for the region near r = 2M. Lines of constant t correspond to straight lines through the origin whose slopes are between -1 and 1, with the X axis corresponding to t = 0. Note that the second and fourth quadrants of this diagram represent negative values of t. Lines of constant r are hyperbolae (in green above). From the indifference of the inverse transformation to sign, we see that the left and right half planes represent a double cover of this diffeomorphism.

In these coordinates (and abbreviating the ProductLog function as P), the Schwarzschild metric is

ds² = 16 M² P ((X² - T²) / e) / ((X² - T²) (1 + P ((X² - T²) / e))) (dX² - dT²) +
4 M² (1 + P ((X² - T²) / e))² (dθ² + sin² (θ) dφ²).

This appears to be singular at X = T (at r = 2M). However, if we parameterize the metric using the function

R (X, T) = 2M (1 + P ((X² - T²) / e))
(implying that X² - T² = e^{R / 2M} (R / 2M - 1)),

the metric takes the simple (and suggestive) form

ds² = 32 e^{-R / 2M} M³ / R (dX² - dT²) + R² (dθ² + sin² (θ) dφ²).

Examining the limit of R (X, T) as T -> X, we find

Limit[ R[X, T], T->X]
2M

The function R is equivalent to the coordinate r in the region r > 2M; we will interpret it as an analytical continuation of r to the region r <= 2M. Lines of constant R in this region are hyperbolae crossing the T axis between the red and blue lines in the diagram above. Because t is infinite on the blue lines, it cannot be continued into that region in the same fashion as R.

This metric has a singularity at R = 0, of which we will say more soon. Of course the metric is only valid outside whatever interior solution is responsible for the curvature; we still expect it to describe a region of topology R⁴ - B⁴, which excludes the point R = 0. So we see that the ball that was not covered by the asymptotically spherical coordinates is not necessarily the interior solution; continuation of the vacuum region for r < 2M requires only a coordinate system capable of covering the entire vacuum region. We will call the singularity at r = 2M a coordinate singularity.

These examples lead us to a notion of "appropriateness" for coordinate charts. Clearly the asymptotically spherical coordinates are appropriate for the Schwarzschild metric for r > 2M, yet those same coordinates are meaningless for r <= 2M. And while Kruskal Coordinates are appropriate for describing the geometry for R < 2M, they are not nearly as useful outside that region as are the asymptotically spherical coordinates.

Because it is not always obvious which manifold is described by a given metric, and because two very different metrics may in fact describe the same geometry, we are led to ask the following questions:

Is there a way to know in advance whether a metric singularity is a coordinate singularity or an essential singularity, which cannot be removed by a coordinate transformation (degeneracy singularities are thankfully obvious) ?

Given two metrics, such as the Schwarzschild metrics in asymptotically spherical coordinates and Kruskal Coordinates, is there any way to determine if they are related by a diffeomorphism?

The answer to the first is yes; to the second, maybe.

Any product of curvature tensors or their derivatives, such that all indices are fully contracted, is invariant with respect to diffeomorphisms. As a scalar, its numerical value does not depend in any way on the coordinate system used to measure it. We have already met one such scalar: R, the scalar curvature. Because it is identically zero for vacuum spacetimes, which includes many metrics of interest, we consider the simplest scalar invariant quadratic in the Riemann tensor, the Kretschmann Invariant:

R^. R = R^{a b c d} R_{a b c d}

For the Schwarzschild metric in asymptotically spherical and Kruskal Coordinates:

R^. R_spherical = 48 M² / r⁶
R^. R_Kruskal = 3 / (4 M⁴ (1 + P((X² - T²) / e))⁶)
= 48 M² / R⁶

So we see that while the algebraic forms of the invariants are very different, there must exist a simple variable substitution which makes the forms equivalent, if they are related by a diffeomorphism. This means that we have an invariant way to characterize metric singularities, and a potential tool for classifying metrics by diffeomorphism class.

Invariants in General

The Kretschmann Invariant is the most widely used invariant, primarily because it is the simplest invariant one can construct which is sensitive to essential singularities in vacuum metrics. There are of course an infinite number of potential curvature invariants which one could construct. For instance, in 4 dimensions, the following invariant [Ciufolini]

*R^. R = ε^{a b c d} R_{a b e f} R_{c d}^{e f}

is proportional to the intrinsic angular momentum of the spacetime. Or consider [Gass]

D R^. D R = D_a R_{b c d e} D^a R^{b c d e}

which vanishes on the ergosphere of a Kerr black hole (in 4 dimensions). Or perhaps [Bicak]

D D R^. D D R ^. D D R ^. D D R =
D_a D_b R_{c d e f} D_g D_h R_{i j k l} D^a D^b R^{c j e l} D^g D^h R^{i d k f}

which is non-vanishing for expanding type N spacetimes. It is clear that we need to quantify the problem of selecting curvature invariants of interest.

The number of independent curvature invariants of order 0 (involving no covariant derivatives) in D > 2 dimensions is

N^D₀ = ( D - 2 ) ( D - 1 ) D ( D + 3 ) / 12

[Haskins], while for order k there are:

N^D_k = D ( k + 1 ) ( D + k + 1 ) ! / ( 2 ( D - 2 ) ! ( k + 3 ) ! )

For some dimensions of interest we have

D N^D₀ N^D₁ N^D₂

3 3 15 27

4 14 60 126

5 40 175 420

6 90 420 1134

7 175 882 2646

8 308 1680 5544

9 504 2970 10692

10 780 4950 19305

11 1155 7865 33033

D	N^D₀	N^D₁	N^D₂
3	3	15	27
4	14	60	126
5	40	175	420
6	90	420	1134
7	175	882	2646
8	308	1680	5544
9	504	2970	10692
10	780	4950	19305
11	1155	7865	33033

The 14 invariants of order 0 in 4 dimensions were first constructed [Witten] using spinor methods and later covariantly [Greenberg] in terms of the Weyl Tensor (C), the traceless portion of the Ricci Tensor (S), the Einstein Curvature Tensor (E) and the dual operator *:

R S^. S^. S^. S
C^. C C^. E^. E
* C^. C * C^. E^. E
C^. C^. C C^. E^. E^. C^. E^. E
* C^. C^. C * C^. E^. E^. C^. E^. E
S^. S C^. E^. E^. C^. E^. E^. C^. E^. E
S^. S^. S * C^. E^. E^. C^. E^. E^. C^. E^. E

We will be interested in curvature invariants which can be consistently compared in diverse dimensions, and unfortunately neither of the methods used to identify independent invariants generalizes well to dimensions other than 4. This leads us to two problems:

Invariants independent in one dimension may not be so in others.

Since ε has D indices, dual invariants only exist in D mod 4 = 0 and in D mod 2 = 0. For example, we can construct:
*R R = ε^{a b c d} R_{a b e f} R_{c d}^{e f}
*R R R R = ε^{a b c d e f g h} R_{a b i j} R_{c d}^{i j} R_{e f k l} R_{g h}^{k l}
(with a maximum of ( D ! ) ( D ( D - 1 ) / 2 )^{( D / 4 )} products)
in D mod 4 = 0 and in D mod 2 = 0 we can construct:
*R *R R = ε^{a b c d} ε^{e f g h} R_{a b i j} R_{e f}^{i j} R_{c d g h}
*R *R R R R = ε^{a b c d e f} ε^{g h i j k l} R_{a b m n} R_{g h o p} R_{c d}^{m n} R_{i j}^{o p} R_{e f k l}
(with a maximum of ( D ! )² products).
This severely limits the invariants we can construct from dual tensors, both because of the lack of a consistent definition from one value of D to another, and from the point of view of computability in a reasonably finite amount of time.

Invariants of Interest to Us

We will therefore somewhat arbitrarily limit ourselves to invariants of up to cubic in R_{a b c d} and linear in R_{a b c d; e}:

R R^{a b c d} R^e_a^f_c R_{b e d f}
R^{a b} R_{a b} R^{a b c d} R^e_a^f_c R_{b f d e}
R^{a b c d} R_{a b c d} R^{a b; c} R_{a b; c}
R^{a b} R^c_a R_{b c} R^{a b; c} R_{a c; b}
R^{a b c d} R_{a c} R_{b d} R^{a b}_{; a} R^c_{b; c}
R^{a b c d} R^e_a R_{b c d e} R^{a b c d; e} R_{a b c d; e}
R^{a b c d} R^{e f}_{a b} R_{c d e f} R^{a b c d}_{; a} R^e_{b c d; e}

ε^{a b c d ...} ε^{e f g h ...} R_{a b e f} R_{c d g h} R... / ((D/2)! (8 π)^D/2)
This is the Euler Class, which is only definable for even D. For a compact manifold, the integral of the Euler Class over the entire manifold is a topological invariant called the Euler Characteristic. Note that the Euler Class includes additional terms for manifolds with boundary.
ε^{a b c i ...} ε^{e f g}_{i ...} R_{b c e}^h R_{f g a h}
= δ^a_[e δ^b_f δ^c_g] R_{b c}^{e h} R^{f g}_{a h}
The following Mathematica code can be used to compute this last invariant:
deltasuuulll = Table[ Table[ Table[ Table[ Table[ Table[ 0,
{i, dim}], {j, dim}], {k, dim}], {l, dim}], {m, dim}], {n, dim}];
deltaul[ a_, b_] := If[a == b, 1, 0];
Do[ Do[ Do[ Do[ Do[ Do[ deltasuuulll[[i, j, k, l, m, n]] =
deltaul[i, l] deltaul[j, m] deltaul[k, n] + deltaul[i, m] deltaul[j, n] deltaul[k, l] +
deltaul[i, n] deltaul[j, l] deltaul[k, m] - deltaul[i, m] deltaul[j, l] deltaul[k, n] -
deltaul[i, l] deltaul[j, n] deltaul[k, m] - deltaul[i, n] deltaul[j, m] deltaul[k, l],
{n, dim}], {m, dim}], {l, dim}], {k, dim}], {j, dim}], {i, dim}];
Rlluu = simpler[ raise[ raise[ Rllll, 3], 4]];
Ruull = simpler[ raise[ raise[ Rllll, 1], 2]];
starRstarR = simpler[ Sum[ Sum[ Sum[ Sum[ Sum[ Sum[ Sum[
deltasuuulll[[aa, bb, cc, ee, ff, gg]] Rlluu[[bb, cc, ee, hh]] Ruull[[ff, gg, aa, hh]],
{hh, dim}], {gg, dim}], {ff, dim}], {ee, dim}], {cc, dim}], {bb, dim}], {aa, dim}]];

For vacuum solutions to Einstein's Equations, we find that

R = 2 D Λ / (D - 2),
R^{a b} R_{a b} = 4 D Λ² / (D - 2)²

and

R^{a b} R^c_a R_{b c} =
R^{a b c d} R_{a c} R_{b d} =
8 D Λ³ / (D - 2)³

by contracting the field equations appropriately.

Another set of invariants of some interest are the Pontrjagin Classes. These are not scalar invariants, but rather differential forms defining a set of characteristic classes of the tangent space manifold. The first Pontrjagin Class is [Eguchi, Gilkey and Hanson]

p₁ = - Tr (R ^ R) / (8 π²)
= - (R^a_{b c d} R^b_{a e f} + R^a_{b e f} R^b_{a c d} -
R^a_{b e d} R^b_{a c f} - R^a_{b f d} R^b_{a e c} -
R^a_{b c e} R^b_{a d f} - R^a_{b c f} R^b_{a e d}) / (48 π²),

a 4-form defined for D >= 4, and the second is

p₂ = Tr (R ^ R ^ R ^ R) / (64 π⁴)
(which has 8 ! / 2⁴ = 2520 terms),

an 8-form defined for D >= 8. p₁ is most useful for compact manifolds in D = 4, where its integral is a topological invariant and an ingredient in various index theorems; it is zero for all of the manifolds we will discuss except the black holes. p₂ is zero for all of the manifolds we will discuss, and is nonzero only for extremely complicated spaces.

The following Mathematica code can be used as a model for computing the first Pontrjagin Class:

wedge[ q1_, aa_, bb_, i_, j_, q2_, cc_, dd_, k_, l_] :=
(q1[[aa, bb, i, j]] q2[[cc, dd, k, l]] + q1[[aa, bb, k, l]] q2[[cc, dd, i, j]] -
q1[[aa, bb, k, j]] q2[[cc, dd, i, l]] - q1[[aa, bb, l, j]] q2[[cc, dd, k, i]] -
q1[[aa, bb, i, k]] q2[[cc, dd, j, l]] - q1[[aa, bb, i, l]] q2[[cc, dd, k, j]]) / 6
If[ (i == k) || (i == l) || (j == k) || (j == l), 0, 1];
pindex[ ii_, jj_Integer] := Block[{inds},
If[ Head[ii] === Integer, If[ jj < ii, jj, jj + 1],
(inds = Select[ Table[ i, {i, dim}], !MemberQ[ ii, #]&];
Return[ inds[[jj]]];)]];
pontrjagin[] := Block[{p1, p2},
(If[ dim < 4, Return[], ];
Switch[ dim,
4, If[ (p1 = simpler[ Sum[ Sum[- wedge[ rulll, aa, bb, 1, 2,
rulll, bb, aa, 3, 4], {bb, dim}], {aa, dim}] / (8 Pi²)]) =!= 0,
Print[ "p1[1, 2, 3, 4] = ", p1], ],
5, Do[ If[ (p1 = simpler[ Sum[ Sum[- wedge[
rulll, aa, bb, pindex[ii, 1], pindex[ii, 2],
rulll, bb, aa, pindex[ii, 3], pindex[ii, 4]],
{bb, dim}], {aa, dim}] / (8 Pi²)]) =!= 0,
Print[ "p1[", pindex[ii, 1], ", ", pindex[ii, 2],
", ", pindex[ii, 3], ", ", pindex[ii, 4], "] = ", p1], ], {ii, dim}],
6, Do[ Do[ If[ (p1 = simpler[ Sum[ Sum[- wedge[
rulll, aa, bb, pindex[{ii, jj}, 1], pindex[{ii, jj}, 2],
rulll, bb, aa, pindex[{ii, jj}, 3], pindex[{ii, jj}, 4]],
{bb, dim}], {aa, dim}] / (8 Pi²)]) =!= 0,
Print[ "p1[", pindex[{ii, jj}, 1], ", ",
pindex[{ii, jj}, 2], ", ", pindex[{ii, jj}, 3], ", ",
pindex[{ii, jj}, 4], "] = ", p1], ],
{jj, ii + 1, dim}], {ii, dim - 1}]];)];

The wedge function computes the wedge product of two 2-forms q1[[ aa, bb]] and q2[[ cc, dd]], whose 2-form indices are {i, j} and {k,l}, respectively. The pindex function chooses a set of 4-form indices for computation, allowing the pontrjagin function to compute only the independent 4-forms in the class. This latter function assumes that the variable dim has been set to the dimension of the manifold in question (as does pindex), and that rulll is the curvature tensor. The generalization to higher dimensions follows the modifications between the cases D = 5 and D = 6 above.

For non-vacuum solutions, there exist invariants of the stress-energy tensor which can be expressed in terms of the invariants above:

T^{a b} T_{a b} = (R^{a b} R_{a b} + R² (D / 4 - 1) - Λ R (D - 2) + D Λ²) / α²
T^{a b} T^c_a T_{b c} = (R^{a b} R^c_a R_{b c} - 3 R (R^{a b} R_{a b} / 2 + Λ² (D / 2 - 1)) +
3 Λ R^{a b} R_{a b} - R³ (D / 8 - 3 / 4) + 3 Λ R² (D / 4 - 1) + Λ³ D) / α³

T^{a b; c} T_{a b; c} = (R^{a b; c} R_{a b; c} + R^{, a} R_{, a} (D / 4 - 1)) / α²
T^{a b; c} T_{a c; b} = (R^{a b; c} R_{a b; c} - R^{, a} R^b_{a; b} + R^{, a} R_{, a} / 4) / α²

T^b_{a; b} is identically zero (conservation of energy), so we also have

R^{a b}_{; a} R^c_{b; c} = R^{, a} R^b_{a; b} - R^{, a} R_{, a} / 4

For a perfect fluid with density ρ, pressure P and velocity v^a,

T^{a b} = ρ v^a v^b + P (g^{a b} + v^a v^b)
T = (ρ + P) v^a v_a + D P
T^{a b} T_{a b} = (ρ + P)² (v^a v_a)² + 2 P (ρ + P) v^a v_a + D P²

and

T^{a b} T^c_a T_{b c} = (ρ + P)³ (v^a v_a)³ + 3 P (ρ + P)² (v^a v_a)² + 3 P² (ρ + P) v^a v_a + D P³

The invariants involving the covariant derivative of T^{a b} for a perfect fluid are sufficiently complex that little is to be learned from their general form.

Of course, we would like the invariants we examine to include those of some physical or intrinsic geometric interest, but in all but the simplest cases it is a priori impossible to determine which those might be. For example, by equating our two expressions for T^{a b} T_{a b}, we see that for D = 4, Λ = 0, and a pressure-less perfect fluid, the square of the Ricci Tensor is equal to the square of the kinetic energy density. But in most cases, we must simply take our chances and see what turns up!

The next section explores spheres in arbitrary dimensions.

Table of Contents

Index:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Please send comments or suggestions to the author.

R	S^. S^. S^. S
C^. C	C^. E^. E
* C^. C	* C^. E^. E
C^. C^. C	C^. E^. E^. C^. E^. E
* C^. C^. C	* C^. E^. E^. C^. E^. E
S^. S	C^. E^. E^. C^. E^. E^. C^. E^. E
S^. S^. S	* C^. E^. E^. C^. E^. E^. C^. E^. E

R	R^{a b c d} R^e_a^f_c R_{b e d f}
R^{a b} R_{a b}	R^{a b c d} R^e_a^f_c R_{b f d e}
R^{a b c d} R_{a b c d}	R^{a b; c} R_{a b; c}
R^{a b} R^c_a R_{b c}	R^{a b; c} R_{a c; b}
R^{a b c d} R_{a c} R_{b d}	R^{a b}_{; a} R^c_{b; c}
R^{a b c d} R^e_a R_{b c d e}	R^{a b c d; e} R_{a b c d; e}
R^{a b c d} R^{e f}_{a b} R_{c d e f}	R^{a b c d}_{; a} R^e_{b c d; e}