Black Holes
The term "black hole" is actually an approximation: barring the existence of so-called "primordial" black holes,
any star which collapses to a surface radius inside its horizon will not appear black
in all wavelengths. Because the gravitational red-shift approaches infinity at the horizon,
it will appear as it did before it collapsed within its
horizon, but in ever-increasing wavelengths. Because no timelike or null geodesics lead out of
the horizon, no experiments can ever be done which will probe the region inside the horizon;
at least, none that can communicate results to anyone outside.
With these provisions, the so-called black hole solutions to
Einstein's Equations are very important
physically for what they predict about the region exterior to the horizon, and very interesting to
contemplate. Because all information about the region interior to the horizon is unavailable to
observers outside, only the globally measurable quantities are experimentally accessible: mass, angular
momentum and charge. The Kerr-Newman Solution to Einstein's Equations describes the spacetime exterior
to any massive charged rotating object with axial symmetry, whether it has collapsed inside its horizon radius
or not. Because of this importance, we will examine it in 4 dimensions in some detail before considering
other dimensions.
The Kerr-Newman metric in D = 4 in (asymptotically flat) Boyer-Lindquist coordinates is
[Wald]
ds2 = (r2 + a2 cos(θ)2) dr2 /
(a2 + e2 + r2 - 2 M r) +
(r2 + a2 cos(θ)2) dθ2 +
((a2 + r2)2 -
a2(a2 + e2 + r2 - 2 M r) sin(θ)2)
sin(θ)2 dφ2 / (r2 + a2 cos(θ)2) +
a (- e2 + 2 M r) sin(θ)2 dφ dt /
(r2 + a2 cos(θ)2) -
(a2 cos(θ)2 + e2 + r2 - 2 M r) dt2 /
(r2 + a2 cos(θ)2)
(our a is the negative of Wald's for compatibility with the Myers-Perry metric below)
The special cases of this metric include
- e = 0, called the Kerr metric;
- a = 0, called the Reissner-Nordstrom metric, and
- e = 0 and a = 0, which is of course the
Schwarzschild metric.
With the usual coordinate transformation
c = cos(θ), the Kerr-Newman metric can be written as
ds2 = (r2 + a2 c2) dr2
/ (a2 + e2 + r2 - 2 M r) +
(r2 + a2 c2) dc2 / (1 - c2) +
(1 - c2) ((a2 + r2)2 -
a2 (1 - c2)(a2 + e2 -2 M r + r2))
dφ2 / (r2 + a2 c2) +
a (1 - c2) (- e2 + 2 M r) dφ dt
/ (r2 + a2 c2) -
(a2 c2 + e2 + r2 - 2 M r) dt2
/ (r2 + a2 c2)
The inverse metric is
|
g r r | (a2 + e2 + r2 - 2 M r) /
(a2 c2 + r2)
|
|
g c c | (1 - c2) /
(a2 c2 + r2)
|
|
g φ φ | (a2 c2 + e2 + r2 - 2 M r) /
((1 - c2) (a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
g φ t | a (-e2 + 2 M r) /
((a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
g t t | - (a4 c2 - a2 e2 + a2 c2 e2 + 2 a2 M r - 2 a2 c2 M r + a2 r2 + a2 c2 r2 + r4) /
|
|
((a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
Killing Vectors and Null Surfaces
Killing Vectors are the generators of symmetries of a spacetime. They obey Killing's Equation:
ka ;b + kb ;a = 0.
We expect that {0,0,1,0} and {0,0,0,1} are Killing Vectors, because the metric is independent of both
φ and t. We can verify this with a simple Mathematica computation:
kvu = { kvr, kvth, kvph, kvt};
kvl = lower[ kvu, 1];
Dkvll = covder[ kvl];
killeq = Table[ Table[ Simplify[ Dkvll[[i,j]] + Dkvll[[j,i]]], {j, 4}], {i, 4}];
killeq /. { kvr -> 0, kvth -> 0}
where "lower" lowers the first (and only) index of the vector kvu, and "covder" returns the
covariant derivative of kvl as a matrix whose
second index corresponds to the derivative index. Examining
the output we see that if both kvr and kvth are set to zero, Killing's Equation is satisfied for any
constant kvph and kvt.
The norm of the asymptotic timelike Killing vector {0,0,0,1} is zero at the
degeneracy singularity
r = M +- (M2 - a2 c2 - e2)1/2,
and it becomes spacelike for smaller values of r.
This surface is called the ergosphere; nothing inside it can remain stationary with respect to the asymptotic
time coordinate, because geodesics parallel to {0,0,0,1} are no longer timelike.
We will define an event horizon as a closed, null 2-surface generated by a Killing Vector.
A null surface is spanned by at least one null vector and no timelike ones.
Because it is a null surface, the light cones of all events on the surface are tangent to the
surface. Because it is generated by a Killing Vector, it is invariant
with respect to the symmetries of the metric. Hence it defines an invariant surface which can be crossed
in only one direction. We can use the following Mathematica code (and some intuition) to
find a Killing Vector which is timelike in the ergosphere but null on the event horizon:
kvu = { 0, 0, phco, 1};
Numerator[ FullSimplify[ Sum[ Sum[ g[[i,j]] kvu[[i]] kvu[[j]], {j, 4}], {i, 4}]]]
- (a2 + e2 - 2 M r +
r2 - (a4 phco2 + phco2 r4 +
2 a phco (e2 - 2 M r) +
a2 (1 + 2 phco2 r2)) Sin[th]2 +
a2 phco2 (a2 + e2 - 2 M r + r2) Sin[th]4)
rsol = Solve[ a2 + e2 - 2 M r + r2 == 0, r]
{{ r -> M - Sqrt[ - a2 - e2 + M2]},
{ r -> M + Sqrt[ - a2 - e2 + M2]}}
Flatten[
Union[ FullSimplify[
Solve[
((a4 phco2 + phco2 r4 +
2 a phco (e2 - 2 M r) +
a2 (1 + 2 phco2 r2)) /.
rsol[[2]]) == 0, phco]]]]
{phco -> - a / (e2 - 2 M (M + Sqrt[ - a2 - e2 + M2]))}
We first construct a linear combination of the two Killing Vectors and find its norm. Since the metric
has a coordinate singularity
where a2 + e2 - 2 M r + r2 is zero, we expect that to be
the location of the event horizon. If it is, the terms in the norm which are constant and quartic in
sin(θ) will vanish, leaving us to find the value of phco which will
make the quadratic term vanish at those values of r. We end up with a Killing Vector which is
null on the surface
r = M + (M2 - a2 - e2)1/2, and timelike everywhere
outside it.
We have actually not proved that the event horizon can only be crossed in one direction, but
an analysis of geodesic motion will confirm our computation of its location. The asymptotic
coordinates fail at the horizon, so we have ignored the inner horizon solution.
A coordinate extension similar to but much more complicated than the
Kruskal Extension is possible
here, and we will assume that for those who wish to contemplate the region interior to the horizon,
the coordinate r is similarly extendible.
Geometry
The nonzero Christoffel Symbols are
|
Γ rr r | (a2 (c2 (M - r) + r) + r (e2 - M r)) /
((a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
Γ rr c | a2 c /
(a2 c2 + r2)
|
|
Γ rc c | - r (a2 + e2 + r2 - 2 M r) /
((1 - c2) (a2 c2 + r2))
|
|
Γ rφ φ | - (1 - c2) (a2 + e2 + r2 - 2 M r) (r5 + a4 (c2 M + c4 (r - M)) + a2 r (((1 - c2) e2) +
|
|
r (2 c2 r - (1 - c2) M))) /
(a2 c2 + r2)3
|
|
Γ rφ t | - a (1 - c2) (a2 + e2 + r2 - 2 M r) (a2 c2 M + r (e2 - M r)) /
(a2 c2 + r2)3
|
|
Γ rt t | - (a2 + e2 + r2 - 2 M r) (a2 c2 M + r (e2 - M r)) /
(a2 c2 + r2)3
|
|
Γ cr r | - a2 c (1 - c2) /
((a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
Γ cr c | r /
(a2 c2 + r2)
|
|
Γ cc c | c (a2 + r2) /
((1 - c2) (a2 c2 + r2))
|
|
Γ cφ φ | c (1 - c2) (a6 c4 + r6 + a2 r2 (-2 (1 - c2) e2 + r (4 M - 4 c2 M + r + 2 c2 r)) +
|
|
a4 (- (1 - c4) e2 + r (2 (1 - c4) M + c2 (2 + c2) r))) /
(a2 c2 + r2)3
|
|
Γ cφ t | - a c (1 - c2) (e2 - 2 M r) (a2 + r2) /
(a2 c2 + r2)3
|
|
Γ ct t | - a2 c (1 - c2) (e2 - 2 M r) /
(a2 c2 + r2)3
|
|
Γ φr φ | (r3 (e2 + r2 - 2 M r) + a4 (c2 M + c4 (- M + r)) + a2 r (e2 + r (- M - c2 M + 2 c2 r))) /
|
|
((a2 c2 + r2)2 (a2 + e2 + r2 - 2 M r))
|
|
Γ φr t | a (a2 c2 M + r (e2 - M r)) /
((a2 c2 + r2)2 (a2 + e2 + r2 - 2 M r))
|
|
Γ φc φ | - c (a4 c4 + r4 + a2 (- (1 - c2) e2 + 2 r (M - c2 M + c2 r))) /
((1 - c2) (a2 c2 + r2)2)
|
|
Γ φc t | a c (e2 - 2 M r) /
((1 - c2) (a2 c2 + r2)2)
|
|
Γ tr φ | - a (1 - c2) (a4 c2 M + r3 (2 e2 - 3 M r) + a2 (1 + c2) r (e2 - M r)) /
|
|
((a2 c2 + r2)2 (a2 + e2 + r2 - 2 M r))
|
|
Γ tr t | - (a2 + r2) (a2 c2 M + r (e2 - M r)) /
((a2 c2 + r2)2 (a2 + e2 + r2 - 2 M r))
|
|
Γ tc φ | - a3 c (1 - c2) (e2 - 2 M r) /
(a2 c2 + r2)2
|
|
Γ tc t | - a2 c (e2 - 2 M r) /
(a2 c2 + r2)2
|
The r-c hypersurface is in general geodesic. For the
non-rotating cases, r is a geodesic direction, and the
r-t, r-c and spacelike hypersurfaces are all geodesic. The fact that the r-t hypersurface is not
geodesic in the rotating case reflects the frame dragging effects mentioned earlier: radial timelike
geodesics do not exist when a is nonzero.
The nonzero components of the Riemann Tensor are
|
R r c r c | (- (a2 c2 e2) + 3 a2 c2 M r + e2 r2 - M r3) /
((1 - c2) (a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
R r c φ t | - a c (a2 c2 M + 2 e2 r - 3 M r2) /
(a2 c2 + r2)2
|
|
R r φ r φ | - (1 - c2) (2 a6 c2 e2 - a6 c4 e2 + a4 c2 e4 - a4 c4 e4 - 9 a6 c2 M r +
6 a6 c4 M r -
|
|
8 a4 c2 e2 M r + 8 a4 c4 e2 M r - 4 a4 e2 r2 +
6 a4 c2 e2 r2 - a4 c4 e2 r2 - 3 a2 e4 r2 +
|
|
3 a2 c2 e4 r2 + 12 a4 c2 M2 r2 -
12 a4 c4 M2 r2 + 3 a4 M r3 - 14 a4 c2 M r3 +
|
|
6 a4 c4 M r3 + 8 a2 e2 M r3 - 8 a2 c2 e2 M r3 - 5 a2 e2 r4 + 4 a2 c2 e2 r4 -
|
|
4 a2 M2 r4 + 4 a2 c2 M2 r4 + 4 a2 M r5 -
5 a2 c2 M r5 - e2 r6 + M r7) /
|
|
((a2 c2 + r2)3 (a2 + e2 + r2 - 2 M r))
|
|
R r φ r t | a (1 - c2) (- 2 a4 c2 e2 - a2 c2 e4 + 9 a4 c2 M r + 8 a2 c2 e2 M r + 4 a2 e2 r2 -
2 a2 c2 e2 r2 +
|
|
3 e4 r2 -
12 a2 c2 M2 r2 - 3 a2 M r3 +
9 a2 c2 M r3 - 8 e2 M r3 + 4 e2 r4 + 4 M2 r4 - 3 M r5) /
|
|
((a2 c2 + r2)3 (a2 + e2 + r2 - 2 M r))
|
|
R r φ c φ | 3 a2 c (1 - c2) (a2 + r2) (a2 c2 M + 2 e2 r - 3 M r2) /
(a2 c2 + r2)3
|
|
R r φ c t | - a c (- 3 a2 + 2 a2 c2 - r2) (a2 c2 M + 2 e2 r - 3 M r2) /
(a2 c2 + r2)3
|
|
R r t r t | - (2 a4 c2 e2 - a4 c4 e2 + a2 c2 e4 - 9 a4 c2 M r + 3 a4 c4 M r - 8 a2 c2 e2 M r - 4 a2 e2 r2 +
|
|
2 a2 c2 e2 r2 - 3 e4 r2 + 12 a2 c2 M2 r2 +
3 a2 M r3 - 7 a2 c2 M r3 + 8 e2 M r3 - 3 e2 r4 -
|
|
4 M2 r4 + 2 M r5) /
((a2 c2 + r2)3 (a2 + e2 + r2 - 2 M r))
|
|
R r t c φ | - a c (- 3 a2 + a2 c2 - 2 r2) (a2 c2 M + 2 e2 r - 3 M r2) /
(a2 c2 + r2)3
|
|
R r t c t | 3 a2 c (a2 c2 M + 2 e2 r - 3 M r2) /
(a2 c2 + r2)3
|
|
R c φ c φ | (4 a6 c2 e2 - a6 c4 e2 + a4 c2 e4 - a4 c4 e4 - 9 a6 c2 M r + 3 a6 c4 M r - 5 a4 c2 e2 M r +
|
|
5 a4 c4 e2 M r - 2 a4 e2 r2 +
8 a4 c2 e2 r2 - a4 c4 e2 r2 - a2 e4 r2 + a2 c2 e4 r2 + 6 a4 c2 M2 r2 -
|
|
6 a4 c4 M2 r2 + 3 a4 M r3 - 16 a4 c2 M r3 + 3 a4 c4 M r3 + 3 a2 e2 M r3 -
3 a2 c2 e2 M r3 - 3 a2 e2 r4 +
|
|
4 a2 c2 e2 r4 - 2 a2 M2 r4 + 2 a2 c2 M2 r4 + 5 a2 M r5 - 7 a2 c2 M r5 - e2 r6 + 2 M r7) /
|
|
(a2 c2 + r2)3
|
|
R c φ c t | - a (- 4 a4 c2 e2 - a2 c2 e4 + 9 a4 c2 M r + 5 a2 c2 e2 M r + 2 a2 e2 r2 - 4 a2 c2 e2 r2 + e4 r2 -
|
|
6 a2 c2 M2 r2 - 3 a2 M r3 + 9 a2 c2 M r3 - 3 e2 M r3 + 2 e2 r4 + 2 M2 r4 - 3 M r5) /
(a2 c2 + r2)3
|
|
R c t c t | (4 a4 c2 e2 - 3 a4 c4 e2 + a2 c2 e4 - 9 a4 c2 M r + 6 a4 c4 M r - 5 a2 c2 e2 M r -
|
|
2 a2 e2 r2 + 2 a2 c2 e2 r2 - e4 r2 + 6 a2 c2 M2 r2 +
|
|
3 a2 M r3 - 5 a2 c2 M r3 + 3 e2 M r3 - e2 r4 - 2 M2 r4 + M r5) /
((1 - c2) (a2 c2 + r2)3)
|
|
R φ t φ t | - (1 - c2) (a2 + e2 + r2 - 2 M r) (- (a2 c2 e2) + 3 a2 c2 M r + e2 r2 - M r3) /
(a2 c2 + r2)3
|
Note that this metric is the first we have considered in which curvature components with more than 2
different indices are nonzero; this is an indication of the complexity of the metric.
The nonzero components of the Ricci Tensor are
|
R r r | - e2 /
((a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
R c c | e2 /
((1 - c2) (a2 c2 + r2))
|
|
R φ φ | - (1 - c2) e2 (- 2 a4 + a4 c2 - a2 e2 + a2 c2 e2 + 2 a2 M r - 2 a2 c2 M r -
|
|
3 a2 r2 + a2 c2 r2 - r4) /
(a2 c2 + r2)3
|
|
R φ t | a (1 - c2) e2 (2 a2 + e2 - 2 M r + 2 r2) /
(a2 c2 + r2)3
|
|
R t t | e2 (2 a2 - a2 c2 + e2 + r2 - 2 M r) /
(a2 c2 + r2)3
|
The vector potential for the charged metric is
AEM =
- a (1 - c2) e r dφ /
(a2 c2 + r2) - e r dt / (a2 c2 + r2)
which gives us the following nonzero components of the electromagnetic field strength tensor
Fa b = da Ab - db Aa :
|
Fr φ | - a (1 - c2) e (r2 - a2 c2) /
(a2 c2 + r2)2
|
|
Fr t | e (a2 c2 - r2) /
(a2 c2 + r2)2
|
|
Fc φ | - 2 a c e r (a2 + r2) /
(a2 c2 + r2)2
|
|
Fc t | - 2 a2 c e r /
(a2 c2 + r2)2
|
and the following components of the stress-energy tensor
Ta b = Fac Fc b - ga b Fc d Fc d / 4 :
|
Tr r | - e2 /
(2 (a2 c2 + r2) (a2 + e2 + r2 - 2 M r))
|
|
Tc c | e2 /
(2 ((1 - c2) (a2 c2 + r2))
|
|
Tφ φ | - (1 - c2) e2 (- 2 a4 + a4 c2 - a2 e2 + a2 c2 e2 + 2 a2 M r - 2 a2 c2 M r -
|
|
3 a2 r2 + a2 c2 r2 - r4) /
(2 (a2 c2 + r2)3)
|
|
Tφ t | a (1 - c2) e2 (2 a2 + e2 - 2 M r + 2 r2) /
(2 (a2 c2 + r2)3)
|
|
Tt t | e2 (2 a2 - a2 c2 + e2 + r2 - 2 M r) /
(2 (a2 c2 + r2)3)
|
The invariants we have chosen to examine are
|
R | 0
|
|
Ra b Ra b | 4 e4 / (a2 c2 + r2)4
|
|
Ra b c d Ra b c d | -8 ( -7 a4 c4 e4 + 6 a6 c6 M2 + 60 a4 c4 e2 M r + 34 a2 c2 e4 r2 -
|
|
90 a4 c4 M2 r2 - 120 a2 c2 e2 M r3 -
|
|
7 e4 r4 + 90 a2 c2 M2 r4 + 12 e2 M r5 - 6 M2 r6) / (a2 c2 + r2)6
|
|
Ra b Rca Rb c | 0
|
|
Ra b c d Ra c Rb d | 16 e4 (a2 c2 e2 - 3 a2 c2 M r - e2 r2 + M r3) / (a2 c2 + r2)7
|
|
Ra b c d Rea Rb c d e | 16 e4 (a2 c2 e2 - 3 a2 c2 M r - e2 r2 + M r3) / (a2 c2 + r2)7
|
|
Ra b c d Re fa b Rc d e f | -96 (a2 c2 e2 - 3 a2 c2 M r - e2 r2 + M r3) ( - 2 a4 c4 e4 +
|
|
3 a6 c6 M2 + 18 a4 c4 e2 M r + 12 a2 c2 e4 r2 -
|
|
27 a4 c4 M2 r2 - 44 a2 c2 e2 M r3 - 2 e4 r4 +
|
|
33 a2 c2 M2 r4 + 2 e2 M r5 - M2 r6) / (a2 c2 + r2)9
|
|
Ra b c d Reafc Rb e d f | -48 (a2 c2 e2 - 3 a2 c2 M r - e2 r2 + M r3) (- a4 c4 e4 +
|
|
3 a6 c6 M2 + 18 a4 c4 e2 M r + 14 a2 c2 e4 r2 -
|
|
27 a4 c4 M2 r2 - 44 a2 c2 e2 M r3 - e4 r4 +
|
|
33 a2 c2 M2 r4 + 2 e2 M r5 - M2 r6) / (a2 c2 + r2)9
|
|
Ra b c d Reafc Rb f d e | -24 (a2 c2 e2 - 3 a2 c2 M r - e2 r2 + M r3) (3 a6 c6 M2 +
|
|
18 a4 c4 e2 M r + 16 a2 c2 e4 r2 - 27 a4 c4 M2 r2 -
|
|
44 a2 c2 e2 M r3 + 33 a2 c2 M2 r4 + 2 e2 M r5 - M2 r6) / (a2 c2 + r2)9
|
|
Ra b; c Ra b; c | -16 e4(-4 a4 c2 + 5 a4 c4 + a2 c2 e2 - 2 a2 c2 M r -
|
|
4 a2 r2 - 5 e2 r2 + 10 M r3 - 5 r4) / (a2 c2 + r2)7
|
|
Ra b; c Ra c; b | -8 e4(-8 a4 c2 + 7 a4 c4 - a2 c2 e2 + 2 a2 c2 M r -
|
|
8 a2 r2 - 7 e2 r2 + 14 M r3 - 7 r4) / (a2 c2 + r2)7
|
|
Ra b; a Rcb; c | 0
|
|
Ra b c d; e Ra b c d; e | 16 (44 a8 c6 e4 - 76 a8 c8 e4 - 32 a6 c6 e6 +
|
|
45 a10 c10 M2 + 45 a8 c8 e2 M2 - 180 a8 c6 e2 M r +
|
|
720 a8 c8 e2 M r + 604 a6 c6 e4 M r - 90 a8 c8 M3 r - 156 a6 c4 e4 r2 +
|
|
712 a6 c6 e4 r2 + 588 a4 c4 e6 r2 -
|
|
1215 a8 c8 M2 r2 - 2340 a6 c6 e2 M2 r2 + 180 a6 c4 e2 M r3 -
|
|
2700 a6 c6 e2 M r3 - 4236 a4 c4 e4 M r3 +
|
|
2520 a6 c6 M3 r3 - 156 a4 c2 e4 r4 - 744 a2 c2 e6 r4 +
|
|
1890 a6 c6 M2 r4 + 9270 a4 c4 e2 M2 r4 +
|
|
324 a4 c2 e2 M r5 - 1332 a4 c4 e2 M r5 + 3540 a2 c2 e4 M r5 -
|
|
6300 a4 c4 M3 r5 + 44 a2 e4 r6 -
|
|
712 a2 c2 e4 r6 + 76 e6 r6 + 1890 a4 c4 M2 r6 -
|
|
5364 a2 c2 e2 M2 r6 - 36 a2 e2 M r7 + 1980 a2 c2 e2 M r7 -
|
|
260 e4 M r7 + 2520 a2 c2 M3 r7 + 76 e4 r8 - 1215 a2 c2 M2 r8 +
|
|
261 e2 M2 r8 - 108 e2 M r9 - 90 M3 r9 +
|
|
45 M2 r10) / (a2 c2 + r2)9
|
|
Ra b c d; a Reb c d; e | -48 e4 (a c - r) (a c + r) (a2 c2 + e2 - 2 M r + r2) / (a2 c2 + r2)7
|
|
Euler class | (-5 a4 c4 e4 + 6 a6 c6 M2 + 60 a4 c4 e2 M r + 38 a2 c2 e4 r2 -
|
|
90 a4 c4 M2 r2 - 120 a2 c2 e2 M r3 -
|
|
5 e4 r4 + 90 a2 c2 M2 r4 + 12 e2 M r5 - 6 M2 r6) / (4 π2 (a2 c2 + r2)6)
|
|
εa b c i ...
εe f gi ...
Rb c eh Rf g a h | -96 (- a2 c2 e2 - a3 c3 M - 2 a c e2 r + 3 a2 c2 M r + e2 r2 + 3 a c M r2 - M r3)
|
|
(a2 c2 e2 - a3 c3 M - 2 a c e2 r - 3 a2 c2 M r - e2 r2 + 3 a c M r2 + M r3) /
|
|
(a2 c2 + r2)6
|
Finally, the first Pontrjagin Class
(p1r c φ t) is
- a c (a2 c2 M + 2 e2 r - 3 M r2)
(- a2 c2 e2 +
3 a2 c2 M r + e2 r2 - M r3) /
(π2 (a2 c2 + r2)5).
The corresponding invariants for the Kerr, Reissner-Nordstrom and Schwarzschild metrics can be
obtained by setting e, a or both to zero, respectively. Note that Ra b c d Ra c Rb d
is equal to Ra b c d Rea Rb c d e, which was true (up to a constant
of proportionality) for the
spheres and cosmological solutions, but not for the
tori.
Those invariants which involve the Ricci Tensor of course vanish for uncharged metrics, as does the square
of the divergence of the Riemann Tensor. The latter invariant also vanishes on the ergosphere. The
Kretschmann Invariant scales as 1 / M4
at the horizon; if we interpret it as the square of the magnitude of the tidal forces,
we see that the more massive
the source object, the larger the horizon radius and the more weak the curvature is there.
It is instructive to examine the invariants computed by Greenberg,
at least to third order:
|
C. C
|
-48 (- a2 c2 e2 + a3 c3 M + 2 a c e2 r + 3 a2 c2 M r +
e2 r2 - 3 a c M r2 - M r3)
|
|
(a2 c2 e2 + a3 c3 M + 2 a c e2 r - 3 a2 c2 M r - e2 r2 -
3 a c M r2 + M r3) / (a2 c2 + r2)6
|
|
|
* C. C
|
192 a c (a2 c2 M + 2 e2 r - 3 M r2)
(- a2 c2 e2 + 3 a2 c2 M r + e2 r2 - M r3) /
(a2 c2 + r2)6
|
|
|
C. C. C
|
96 (- a2 c2 e2 + 3 a2 c2 M r + e2 r2 - M r3)
(- a4 c4 e4 + 3 a6 c6 M2 + 18 a4 c4 e2 M r +
14 a2 c2 e4 r2 - 27 a4 c4 M2 r2 - 44 a2 c2 e2 M r3 -
e4 r4 + 33 a2 c2 M2 r4 + 2 e2 M r5 - M2 r6) /
(a2 c2 + r2)9
|
|
|
* C. C. C
|
192 a c (a2 c2 M + 2 e2 r - 3 M r2)
(-3 a4 c4 e4 + a6 c6 M2 + 22 a4 c4 e2 M r +
10 a2 c2 e4 r2 - 33 a4 c4 M2 r2 - 36 a2 c2 e2 M r3 -
3 e4 r4 + 27 a2 c2 M2 r4 + 6 e2 M r5 - 3 M2 r6) /
(a2 c2 + r2)9
|
|
|
S. S
|
4 e4 / (a2 c2 + r2)4
|
|
|
S. S. S
|
0
|
|
|
C. E. E
|
32 e4 (a2 c2 e2 - 3 a2 c2 M r - e2 r2 + M r3) / (a2 c2 + r2)7
|
|
|
* C. E. E
|
-64 a c e4 (a2 c2 M + 2 e2 r - 3 M r2) /
(a2 c2 + r2)7
|
Note that S S is equal to the square of the Ricci Tensor, and S S S is equal to its cube because,
of course, R = 0. Note too that C E E is equal to 2 Ra b c d Ra c Rb d
and C C C is equal to the cube of the Riemann Tensor. Finally, *C C is proportional to the first
Pontrjagin Class. In the Kerr limit, of course, the Riemann Tensor is equal to the Weyl Tensor
with obvious implications for these invariants.
All invariants involving the dual of the Weyl tensor are proportional to a, and of course all
invariants involving S and E vanish in the Kerr limit. C C has real zeroes in the Kerr limit at
r = +- a c, and (+-2 +- 31/2) a c.
The invariants *C C, *C C C and *C E E all have zeroes at
r = (e2 +- (e4 + 3 a2 c2 M2)1/2) / (3 M)
= +- a c / 31/2 in the Kerr limit
and the invariants *C C, C C C and C E E all have zeroes in the Kerr limit at
r = 0 and +- 31/2 a c.
Higher-dimensional Kerr Solutions
It is possible to construct Kerr metrics in dimensions greater than 4
[Myers].
The geometry of these metrics might be described as squashed SD-4 x "quasi-Kerr"4.
The SD-4 coordinates are {θi,
φ2} and the
"quasi-Kerr"4 coordinates are {r, θ, φ, t},
with the following chart:
θ ∈ (0, π / 2)
θi ∈ (0, π),
φ and φ2 ∈ (0, 2π)
The squashing factor is r2 cos2 (θ)
and the Kerr parameters are μ and a, which we will relate to the mass and
angular momentum presently. Let
ρ2 = r2 + a2
cos2 (θ)
Δ(D) = μ / (rD-5
ρ2)
ψ(D) = ρ2 /
((r2 + a2) - μ / rD-5)
Then the metric in D dimensions is
ds2 = r2 cos2 (θ) dΩ2 +
ψ(D) dr2 +
ρ2 dθ2 +
((r2 + a2) sin2 (θ) +
Δ(D) a2 sin4 (θ))
dφ2 +
2 Δ(D) a sin2 (θ)
dφ dt +
(Δ(D) - 1) dt2
where dΩ2 is the standard metric on SD-4.
Normalizing the Komar integrals for J and M by 4 Ω (where Ω
is the area of a solid angle in D dimensions), we find that
J = a μ / 2
and
M = (D - 3) J / a
We have analyzed these metrics for D = 4 through 11, and found that they have the following properties:
| D |
Horizons exist at zeroes of |
Ergospheres are located at zeroes of |
volume element |
area of a surface of constant r |
|---|
| 4 |
a2 + r (-μ + r) |
-a2 c2 + μ r - r2 |
a2 c2 + r2 |
4 π (a2 + 3 r2) / 3 |
| 5 |
a2 - μ + r2 |
-a2 c2 + μ - r2 |
c r (a2 c2 + r2) |
π2 r (a2 + 2 r2) |
| 6 |
-μ + a2 r + r3 |
μ - r (a2 c2 + r2) |
c2 r2 (a2 c2 + r2) |
8 π2 r2 (3 a2 + 5 r2) / 15 |
| 7 |
-μ + a2 r2 + r4 |
μ - r2 (a2 c2 + r2) |
c3 (1 - c12)1/2 r3 |
π3 r3 (2 a2 + 3 r2) / 3 |
| | |
(a2 c2 + r2) | |
| 8 |
-μ + a2 r3 + r5 |
μ - r3 (a2 c2 + r2) |
c4 (1 - c12) (1 - c22)1/2 |
16 π3 r4 (5 a2 + 7 r2) / 105 |
| | |
r4 (a2 c2 + r2) | |
| 9 |
-μ + a2 r4 + r6 |
μ - r4 (a2 c2 + r2) |
c5 (1 - c12)3/2 (1 - c2)2 |
π4 r5 (3 a2 + 4 r2) / 12 |
| | |
(1 - c32)1/2 r5 (a2 c2 + r2) | |
| 10 |
-μ + a2 r5 + r7 |
μ - r5 (a2 c2 + r2) |
c6 (1 - c12)2 (1 - c22)3/2 |
32 π4 r6 (7 a2 + 9 r2) / 945 |
| | |
(1 - c32) (1 - c42)1/2 | |
| | |
r6 (a2 c2 + r2) | |
| 11 |
-μ + r6 (a2 + r2) |
μ - r6 (a2 c2 + r2) |
c7 (1 - c12)5/2 (1 - c22)2 |
π5 r7 (4 a2 + 5 r2) / 60 |
| | |
(1 - c32)3/2 (1 - c42) | |
| | |
(1 - c52)1/2 r7 (a2 c2 + r2) | |
In the limit a -> 0, the area of a surface of constant r goes to that of flat space, the
locations of the horizons go to those of the Schwarzschild metric in D dimensions and the
curvature invariants go to those of the Schwarzschild metric in D dimensions,
but the metric itself does NOT go to the Schwarzschild metric in D-dimensional asymptotically
spherical coordinates.
We would like to find a coordinate system in which the KerrD metrics go to the
SchwarzschildD metrics in that limit. The key is to examine the different parameterizations of the
D-2 spherical portion of each metric. By explicitly embedding each parameterization into a D-1 Euclidean space
and setting the resultant metrics equal to each other, we can find the appropriate coordinate
transformation using Mathematica:
sphcart[ n_, args_] := Block[ {},(
k = 1;
retab = {};
Do[ (prod = 1;
Do[ prod *= If[ i == k, Cos, Sin][args[[i]]], {i, k}];
AppendTo[ retab, prod];), {k, n}];
AppendTo[ retab, Last[retab] /. Cos[ args[[n]]] -> Sin[ args[[n]]]];
Return[ retab];
)];
dim = 5;
xs = Flatten[ {r, Table[ Symbol[ "t" <> ToString[i]], {i, dim - 3}], phs, t}]
{r,t1,t2,phs,t}
xk = Flatten[ {Table[ Symbol[ "tk" <> ToString[i]], {i, dim - 5}],
If[ dim >= 5, ph2, {}], r, th, phk, t}]
{ph2, r, th, phk, t}
fns = Table[ Apply[ xs[[i]], Join[ {th,phk}, Take[ xk, {1, dim - 4}]]], {i, 2, dim - 1}]
{t1[th, phk, ph2], t2[th, phk, ph2], phs[th, phk, ph2]}
xkcart = Flatten[ {r * Cos[th] sphcart[ dim - 4, Take[ xk, dim - 4]],
r * Sin[th] Cos[phk],
r * Sin[th] Sin[phk]}]
{r Cos[ph2] Cos[th], r Cos[th] Sin[ph2], r Cos[phk] Sin[th],
r Sin[phk] Sin[th]}
xscart = r * sphcart[ dim - 2, fns]
{r Cos[t1[th, phk, ph2]], r Cos[t2[th, phk, ph2]] Sin[t1[th, phk, ph2]],
r Cos[phs[th, phk, ph2]] Sin[t1[th, phk, ph2]] Sin[t2[th, phk, ph2]],
r Sin[phs[th, phk, ph2]] Sin[t1[th, phk, ph2]] Sin[t2[th, phk, ph2]]}
sol = PowerExpand[
FullSimplify[
Solve[ Take[ Thread[ xkcart == xscart], dim - 2], fns][[28]]]]
{phs[th, phk, ph2] -> phk,
t2[th, phk, ph2] ->
ArcCos[Cos[th] Sin[ph2] / Sqrt[1 - Cos[ph2]2 Cos[th]2]],
t1[th, phk, ph2] -> ArcCos[Cos[ph2] Cos[th]]}
First we define a function sphcart, which accepts two arguments: the dimension of a sphere, and
the arguments to the sin and cos functions which will appear in the
Cartesian parameterization of the unit
sphere of that dimension, which is the function output. We then set dim equal to D of the KerrD
metric we are interested in, and define xs and xk as the coordinates of the Schwarzschild and Kerr
metrics in D dimensions, respectively. fns is the Schwarzschild coordinates as functions of the Kerr
coordinates. xkcart and xscart are the Cartesian embeddings of the spherical portions of the Kerr and
Schwarzschild metrics, respectively, and sol is one solution of the 32 obtained by setting the two
embeddings equal to each other and solving for fns. We chose this particular solution for the simplicity
of its signs; the other solutions differed only by relative signs of some of the functions and/or
their arguments.
This process can be repeated in any dimension, and from it we can abstract the required
transformation as follows:
consider a coordinate transformation to {r, θ'i,
φ, t}:
θ = cos-1 ( Sqrt (
cos2 (θ'1) +
sin2 (θ'1) (
cos2 (θ'2) +
sin2 (θ'2) (
...
+ sin2 (θ'D-4)
cos2 (θ'D-3)
))))
θi = cos-1 (
cos (θ'i) / Sqrt (
cos2 (θ'i) +
sin2 (θ'i) (
...
+ sin2 (θ'D-4)
cos2 (θ'D-3)
))))
φ2 = cos-1 (
cos (θ'D-4) / Sqrt (
cos2 (θ'D-4)
+ sin2 (θ'D-4)
cos2 (θ'D-3)
))))
The resulting metric is of the form
ds'2 = dS'2 +
f(r, θ'i) dr2 +
h(r, θ'i) dφ2 +
2 p(r, θ'i) dφ dt +
q(r, θ'i) dt2
where dS'2 has NO nonzero elements! But in the limit a -> 0,
ds'2 becomes the Schwarzschild metric in D-dimensional
asymptotically spherical coordinates.
The following Mathematica code can be used to implement the coordinate transformation in any dimension, and
show the equivalence in the limit a -> 0:
xku = Flatten[ {Table[ Symbol["tk" <> ToString[i]], {i,dim - 5}], If[dim >= 5, ph2, {}], r, th, phk, t}];
rho = Sqrt[ r^2 + a^2 Cos[th]^2];
delta = mu / (r^(dim - 5) rho^2);
psi = r^(dim - 5) rho^2 / (r^(dim - 5) (r^2 + a^2) - mu);
gkll = 0*IdentityMatrix[dim];
Do[
gkll[[i, i]] = r^2 Cos[th]^2 Product[ Sin[ xku[[j - 1]]]^2, {j, 2, i}],
{i, dim - 4}];
gkll[[dim - 3, dim - 3]] = psi;
gkll[[dim - 2, dim - 2]] = rho^2;
gkll[[dim - 1, dim - 1]] = (r^2 + a^2) Sin[th]^2 + delta * a^2 Sin[th]^4;
gkll[[dim - 1, dim]] = delta * a * Sin[th]^2;
gkll[[dim, dim - 1]] = gkll[[dim - 1, dim]];
gkll[[dim, dim]] = -1 + delta;
gkll = simpler[gkll];
gksll = Simplify[ gkll /. a -> 0];
xsu = Flatten[ {r, Table[ Symbol["t" <> ToString[i]], {i,dim - 3}], phs, t}];
f[r] = 1 - mu / r^(dim - 3);
gsll = 0*IdentityMatrix[dim];
Do[
gsll[[i, i]] = r^2 Product[ Sin[xsu[[j]]]^2, {j, 2, i - 1}],
{i, 2, dim - 1}];
gsll[[1, 1]] = 1 / f[r];
gsll[[dim, dim]] = -f[r];
gsll = simpler[gsll];
fns = Flatten[ {
Table[ Apply[xku[[i]], Take[xsu, {2, dim - 1}]], {i, dim - 4}],
Table[ Apply[xku[[i]], Take[xsu, {2, dim - 1}]], {i, dim - 2, dim - 1}]}];
xkcart = Flatten[ {
r * Cos[fns[[dim - 3]]] sphcart[dim - 4, fns],
r * Sin[fns[[dim - 3]]] Cos[fns[[dim - 2]]],
r * Sin[fns[[dim - 3]]] Sin[fns[[dim - 2]]]}];
Print["Check: ", Simplify[ Sum[xkcart[[i]]^2, {i, dim - 1}] == r^2]];
xscart = r * sphcart[dim - 2, Take[xsu, {2,dim - 1}]];
Print["Check: ", Simplify[ Sum[xscart[[i]]^2, {i, dim - 1}] == r^2]];
csexpr[nav_, stop_, ii_] :=
If[ii == stop, Cos[xsu[[nav - ii + stop + 1]]]^2,
csexpr[nav, stop, ii - 1] Sin[xsu[[nav - ii + stop + 1]]]^2 + Cos[xsu[[nav - ii + stop + 1]]]^2];
rules[] := Flatten[{ Table[
fns[[i]] -> ArcCos[ Cos[xsu[[i + 1]]] / Sqrt[ csexpr[dim - 3, i, dim - 3]]],
{i, dim - 4}],
fns[[dim - 3]] -> ArcCos[ Sqrt[ csexpr[dim - 3, 1, dim - 3]]],
fns[[dim - 2]] -> phs}];
Print["Using ", rules[]];
Print["Check: ", PowerExpand[ Simplify[
((xkcart == xscart) /. rules[]) //.
Sqrt[x_] Sqrt[y_] -> Sqrt[ Simplify[x * y]]] //.
Sqrt[x_] / Sqrt[y_] -> Sqrt[ Simplify[x / y]]]];
Print["Xform check: ", Simplify[ (
(gksll = Simplify[ coordxform[gkll, xku, (xku /. Thread[Head /@ fns -> fns]) /. rules[], xsu]]) /. a -> 0)
== gsll]];
The variables xku and gkll correspond to the KerrD metric in the original coordinates,
while xsu and gsll correspond to the Schwarzschild metric in asymptotically spherical
coordinates. The variable gksll is the KerrD metric in the limit a->0, and the "cart" suffix
indicates the use of Cartesian Coordinates. As before, the sphcart function generates
a list of Cartesian Coordinates
as functions of the asymptotically spherical coordinates. The function csexpr recursively
generates the expressions
used to create the coordinate transformation rules by the function "rules".
The replacement operators "//." involving the square
roots are there to simplify expressions that Mathematica should perhaps handle automatically but doesn't.
Invariants for KerrD
We present here the nonzero invariants for the KerrD metrics
(of those we have chosen to examine) for D = 4 to 11:
| D | Ra b c d Ra b c d |
|---|
| 4 | - 12 μ2 (a c - r) (a c + r) (a2 c2 - 4 a c r + r2) (a2 c2 + 4 a c r + r2) / |
| (a2 c2 + r2)6 |
| 5 | 24 μ2 (a2 c2 - 3 r2) (3 a2 c2 - r2) / |
| (a2 c2 + r2)6 |
| 6 | 12 μ2 (a8 c8 + 5 a6 c6 r2 + 11 a4 c4 r4 - 5 a2 c2 r6 + 20 r8) / |
| r6 (a2 c2 + r2)6 |
| 7 | 24 μ2 (3 a8 c8 + 15 a6 c6 r2 + 30 a4 c4 r4 + 27 a2 c2 r6 + 25 r8) / |
| r8 (a2 c2 + r2)6 |
| 8 | 12 μ2 (20 a8 c8 + 99 a6 c6 r2 + 195 a4 c4 r4 + 189 a2 c2 r6 + 105 r8) / |
| r10 (a2 c2 + r2)6 |
| 9 | 24 μ2 (25 a8 c8 + 122 a6 c6 r2 + 235 a4 c4 r4 + 220 a2 c2 r6 + 98 r8) / |
| r12 (a2 c2 + r2)6 |
| 10 | 12 μ2 (105 a8 c8 + 505 a6 c6 r2 + 951 a4 c4 r4 + 855 a2 c2 r6 + 336 r8) / |
| r14 (a2 c2 + r2)6 |
| 11 | 24 μ2 (98 a8 c8 + 465 a6 c6 r2 + 858 a4 c4 r4 + 745 a2 c2 r6 + 270 r8) / |
| r16 (a2 c2 + r2)6 |
| D | Ra b c d Re fa b Rc d e f |
|---|
| 4 | 12 μ3 r (3 a2 c2 - r2) (3 a6 c6 - 27 a4 c4 r2 + 33 a2 c2 r4 - r6) / |
| (a2 c2 + r2)9 |
| 5 | - 192 μ3 (a c - r) (a c + r) (a2 c2 - 2 a c r - r2) (a2 c2 + 2 a c r - r2) / |
| (a2 c2 + r2)9 |
| 6 | 12 μ3 (a12 c12 + 4 a10 c10 r2 - 28 a6 c6 r6 + 21 a4 c4 r8 - 80 a2 c2 r10 + 130 r12) / |
| r9 (a2 c2 + r2)9 |
| 7 | 24 μ3 (8 a12 c12 + 57 a10 c10 r2 + 186 a8 c8 r4 + 382 a6 c6 r6 + |
| 576 a4 c4 r8 + 513 a2 c2 r10 + 310 r12) / |
| r12 (a2 c2 + r2)9 |
| 8 | 12 μ3 (130 a12 c12 + 996 a10 c10 r2 + 3387 a8 c8 r4 + 6676 a6 c6 r6 + |
| 8212 a4 c4 r8 + 5936 a2 c2 r10 + 2135 r12) / |
| r15 (a2 c2 + r2)9 |
| 9 | 48 μ3 (155 a12 c12 + 1180 a10 c10 r2 + 3906 a8 c8 r4 + 7264 a6 c6 r6 + |
| 8079 a4 c4 r8 + 5116 a2 c2 r10 + 1484 r12) / |
| r18 (a2 c2 + r2)9 |
| 10 | 12 μ3 (2135 a12 c12 + 15960 a10 c10 r2 + 51270 a8 c8 r4 + 91084 a6 c6 r6 + |
| 94887 a4 c4 r8 + 55188 a2 c2 r10 + 14196 r12) / |
| r21 (a2 c2 + r2)9 |
| 11 | 24 μ3 (2968 a12 c12 + 21777 a10 c10 r2 + 68160 a8 c8 r4 + 116886 a6 c6 r6 + |
| 116228 a4 c4 r8 + 63745 a2 c2 r10 + 15180 r12) / |
| r24 (a2 c2 + r2)9 |
| D | Ra b c d Reafc Rb e d f |
|---|
| 4 | 6 μ3 r (3 a2 c2 - r2) (3 a6 c6 - 27 a4 c4 r2 + 33 a2 c2 r4 - r6) / |
| (a2 c2 + r2)9 |
| 5 | - 96 μ3 (a c - r) (a c + r) (a2 c2 - 2 a c r - r2) (a2 c2 + 2 a c r - r2) / |
| (a2 c2 + r2)9 |
| 6 | 6 μ3 (a12 c12 + 10 a10 c10 r2 + 43 a8 c8 r4 + 100 a6 c6 r6 + |
| 127 a4 c4 r8 - 110 a2 c2 r10 + 85 r12) / |
| r9 (a2 c2 + r2)9 |
| 7 | 6 μ3 (16 a12 c12 + 129 a10 c10 r2 + 438 a8 c8 r4 + 782 a6 c6 r6 + |
| 720 a4 c4 r8 + 297 a2 c2 r10 + 290 r12) / |
| r12 (a2 c2 + r2)9 |
| 8 | 6 μ3 (85 a12 c12 + 636 a10 c10 r2 + 1992 a8 c8 r4 + 3316 a6 c6 r6 + |
| 3097 a4 c4 r8 + 1736 a2 c2 r10 + 770 r12) / |
| r15 (a2 c2 + r2)9 |
| 9 | 12 μ3 (145 a12 c12 + 1040 a10 c10 r2 + 3122 a8 c8 r4 + 5028 a6 c6 r6 + |
| 4673 a4 c4 r8 + 2612 a2 c2 r10 + 868 r12) / |
| r18 (a2 c2 + r2)9 |
| 10 | 12 μ3 (385 a12 c12 + 2685 a10 c10 r2 + 7845 a8 c8 r4 + 12362 a6 c6 r6 + |
| 11331 a4 c4 r8 + 6129 a2 c2 r10 + 1743 r12) / |
| r21 (a2 c2 + r2)9 |
| 11 | 6 μ3 (1736 a12 c12 + 11865 a10 c10 r2 + 34008 a8 c8 r4 + 52710 a6 c6 r6 + |
| 47572 a4 c4 r8 + 24905 a2 c2 r10 + 6420 r12) / |
| r24 (a2 c2 + r2)9 |
| D | Ra b c d Reafc Rb f d e |
|---|
| 4 | 3 μ3 r (3 a2 c2 - r2) (3 a6 c6 - 27 a4 c4 r2 + 33 a2 c2 r4 - r6) / |
| (a2 c2 + r2)9 |
| 5 | - 48 μ3 (a c - r) (a c + r) (a2 c2 - 2 a c r - r2) (a2 c2 + 2 a c r - r2) / |
| (a2 c2 + r2)9 |
| 6 | 3 μ3 (a12 c12 + 16 a10 c10 r2 + 86 a8 c8 r4 + 228 a6 c6 r6 + |
| 233 a4 c4 r8 - 140 a2 c2 r10 + 40 r12) / |
| r9 (a2 c2 + r2)9 |
| 7 | 24 μ3 (2 a12 c12 + 18 a10 c10 r2 + 63 a8 c8 r4 + 100 a6 c6 r6 + |
| 36 a4 c4 r8 - 54 a2 c2 r10 - 5 r12) / |
| r12 (a2 c2 + r2)9 |
| 8 | 3 μ3 (40 a12 c12 + 276 a10 c10 r2 + 597 a8 c8 r4 - 44 a6 c6 r6 - |
| 2018 a4 c4 r8 - 2464 a2 c2 r10 - 595 r12) / |
| r15 (a2 c2 + r2)9 |
| 9 | - 24 μ3 (5 a12 c12 + 70 a10 c10 r2 + 392 a8 c8 r4 + 1118 a6 c6 r6 + |
| 1703 a4 c4 r8 + 1252 a2 c2 r10 + 308 r12) / |
| r18 (a2 c2 + r2)9 |
| 10 | - 3 μ3 (595 a12 c12 + 5220 a10 c10 r2 + 19890 a8 c8 r4 + 41636 a6 c6 r6 + |
| 49563 a4 c4 r8 + 30672 a2 c2 r10 + 7224 r12) / |
| r21 (a2 c2 + r2)9 |
| 11 | - 48 μ3 (154 a12 c12 + 1239 a10 c10 r2 + 4269 a8 c8 r4 + 8022 a6 c6 r6 + |
| 8582 a4 c4 r8 + 4855 a2 c2 r10 + 1095 r12) / |
| r24 (a2 c2 + r2)9 |
| D | Ra b c d; e Ra b c d; e |
|---|
| 4 | 180 μ2 (a2 c2 - μ r + r2) (a4 c4 + 4 a3 c3 r - 6 a2 c2 r2 - 4 a c r3 + r4) |
| (a4 c4 - 4 a3 c3 r - 6 a2 c2 r2 + 4 a c r3 + r4) / |
| (a2 c2 + r2)9 |
| 5 | - 192 μ2 ( -5 a8 c6 + 9 a8 c8 - 4 a6 c6 μ + 9 a6 c4 r2 - 54 a6 c6 r2 + 49 a4 c4 μ r2 + |
| 9 a4 c2 r4 - 58 a2 c2 μ r4 - 5 a2 r6 + 54 a2 c2 r6 + 9 μ r6 - 9 r8) / |
| (a2 c2 + r2)9 |
| 6 | 12 μ2 ( -15 a12 c12 μ + 15 a14 c12 r - 112 a10 c10 μ r2 + |
| 120 a12 c10 r3 + 7 a12 c12 r3 - 358 a8 c8 μ r4 + 407 a10 c8 r5 + 63 a10 c10 r5 - |
| 644 a6 c6 μ r6 + 792 a8 c6 r7 + 210 a8 c8 r7 - 903 a4 c4 μ r8 + 525 a6 c4 r9 + |
| 1022 a6 c6 r9 + 700 a2 c2 μ r10 + 560 a4 c2 r11 - 357 a4 c4 r11 - 700 μ r12 + |
| 525 a2 r13 - 525 a2 c2 r13 + 700 r15) / |
| r9 (a2 c2 + r2)9 |
| 7 | 576 μ2 ( -3 a12 c12 μ + 3 a14 c12 r2 - 22 a10 c10 μ r2 + |
| 23 a12 c10 r4 + 2 a12 c12 r4 - 69 a8 c8 μ r4 + 75 a10 c8 r6 + 16 a10 c10 r6 - |
| 120 a6 c6 μ r6 + 135 a8 c6 r8 + 54 a8 c8 r8 - 124 a4 c4 μ r8 + 140 a6 c4 r10 + |
| 104 a6 c6 r10 - 64 a2 c2 μ r10 + 102 a4 c2 r12 + 86 a4 c4 r12 - 50 μ r12 + |
| 42 a2 r14 + 72 a2 c2 r14 + 50 r16) / |
| r12 (a2 c2 + r2)9 |
| 8 | 12 μ2 ( -700 a12 c12 μ - 5060 a10 c10 μ r2 + |
| 700 a14 c12 r3 - 15631 a8 c8 μ r4 + 5220 a12 c10 r5 + 540 a12 c12 r5 - 26724 a6 c6 μ r6 + |
| 16560 a10 c8 r7 + 4131 a10 c10 r7 - 27222 a4 c4 μ r8 + 28936 a8 c6 r9 + 13419 a8 c8 r9 - |
| 16464 a2 c2 μ r10 + 29916 a6 c4 r11 + 24030 a6 c6 r11 - 6615 μ r12 + 18900 a4 c2 r13 + |
| 24786 a4 c4 r13 + 5880 a2 r15 + |
| 17199 a2 c2 r15 + 6615 r17) / |
| r15 (a2 c2 + r2)9 |
| 9 | 960 μ2 ( -30 a12 c12 μ - 214 a10 c10 μ r2 + |
| 30 a14 c12 r4 - 651 a8 c8 μ r4 + 219 a12 c10 r6 + 25 a12 c12 r6 - 1092 a6 c6 μ r6 + |
| 679 a10 c8 r8 + 186 a10 c10 r8 - 1085 a4 c4 μ r8 + 1155 a8 c6 r10 + 588 a8 c8 r10 - |
| 632 a2 c2 μ r10 + 1155 a6 c4 r12 + 1022 a6 c6 r12 - 196 μ r12 + 670 a4 c2 r14 + |
| 1047 a4 c4 r14 + 180 a2 r16 + 648 a2 c2 r16 + 196 r18) / |
| r18 (a2 c2 + r2)9 |
| 10 | 36 μ2 ( -2205 a12 c12 μ - 15540 a10 c10 μ r2 - |
| 46590 a8 c8 μ r4 + 2205 a14 c12 r5 - 76692 a6 c6 μ r6 + 15820 a12 c10 r7 + |
| 1925 a12 c12 r7 - 74173 a4 c4 μ r8 + 48105 a10 c8 r9 + 14025 a10 c10 r9 - |
| 41184 a2 c2 μ r10 + 79920 a8 c6 r11 + 43362 a8 c8 r11 - 11088 μ r12 + 77407 a6 c4 r13 + |
| 73458 a6 c6 r13 + 42372 a4 c2 r15 + 72985 a4 c4 r15 + 10395 a2 r17 + |
| 41877 a2 c2 r17 + 11088 r19) / |
| r21 (a2 c2 + r2)9 |
| 11 | 192 μ2 ( -980 a12 c12 μ - 6832 a10 c10 μ r2 - |
| 20213 a8 c8 μ r4 + 980 a14 c12 r6 - 32704 a6 c6 μ r6 + 6930 a12 c10 r8 + 882 a12 c12 r8 - |
| 30863 a4 c4 μ r8 + 20727 a10 c8 r10 + 6318 a10 c10 r10 - |
| 16450 a2 c2 μ r10 + 33747 a8 c6 r12 + 19170 a8 c8 r12 - |
| 4050 μ r12 + 31815 a6 c4 r14 + 31752 a6 c6 r14 + 16695 a4 c2 r16 + 30618 a4 c4 r16 + |
| 3850 a2 r18 + 16650 a2 c2 r18 + 4050 r20) / |
| r24 (a2 c2 + r2)9 |
| D | Euler Class |
|---|
| 4 | 3 μ2 (a c - r) (a c + r) (a2 c2 - 4 a c r + r2) (a2 c2 + 4 a c r + r2) / |
| (8 π2 (a2 c2 + r2)6) |
| 6 | μ3 (6 a6 c6 + 31 a4 c4 r2 + 60 a2 c2 r4 - 45 r6) / |
| (8 π3 r7 (a2 c2 + r2)7) |
| 8 | 3 μ4 (117 a6 c6 + 269 a4 c4 r2 - 133 a2 c2 r4 - 525 r6) / |
| (32 π4 r18 (a2 c2 + r2)8) |
| 10 | 45 μ5 (65 a6 c6 + 60 a4 c4 r2 - 243 a2 c2 r4 - 294 r6) / |
| (32 π5 r33 (a2 c2 + r2)9) |
| D | εa b c ... εe f g...
Rb c eh Rf g a h |
|---|
| 4 | - 24 μ2 (a c - r) (a c + r) (a2 c2 - 4 a c r + r2) (a2 c2 + 4 a c r + r2) / |
| (a2 c2 + r2)6 |
| 5 | 96 μ2 (a2 c2 - 3 r2) (3 a2 c2 - r2) / |
| (a2 c2 + r2)6 |
| 6 | 144 μ2 (a8 c8 + 5 a6 c6 r2 + 11 a4 c4 r4 - 5 a2 c2 r6 + 20 r8) / |
| r6 (a2 c2 + r2)6 |
| 7 | 1152 μ2 (3 a8 c8 + 15 a6 c6 r2 + 30 a4 c4 r4 + 27 a2 c2 r6 + 25 r8) / |
| r8 (a2 c2 + r2)6 |
| 8 | 2880 μ2 (20 a8 c8 + 99 a6 c6 r2 + 195 a4 c4 r4 + 189 a2 c2 r6 + 105 r8) / |
| r10 (a2 c2 + r2)6 |
| 9 | 34560 μ2 (25 a8 c8 + 122 a6 c6 r2 + 235 a4 c4 r4 + 220 a2 c2 r6 + 98 r8) / |
| r12 (a2 c2 + r2)6 |
| 10 | 120960 μ2 (105 a8 c8 + 505 a6 c6 r2 + 951 a4 c4 r4 + 855 a2 c2 r6 + 336 r8) / |
| r14 (a2 c2 + r2)6 |
| 11 | 193536 μ2 (98 a8 c8 + 465 a6 c6 r2 + 858 a4 c4 r4 + 745 a2 c2 r6 + 270 r8) / |
| r16 (a2 c2 + r2)6 |
As mentioned above, all invariants depending on Ra b and Ra b c d; a are zero.
All invariants depend only on r, c and the Kerr parameters, and
Ra b c d; e Ra b c d; e vanishes on the ergosphere for D = 4 only.
The last invariant examined is an integer multiple of the Kretschmann Invariant.
All of the invariants demonstrate the essential singularity
at the zero of r2 + a2 c2, commonly called the "ring singularity", and for
D > 5, r = 0 is an essential singularity as well. We suspect that this means that the
Kruskal Extensions for
these metrics are topologically different from those for Kerr4 and Kerr5.
We note that
Ra b c d Re fa b Rc d e f +
4 (Ra b c d Reafc Rb f d e -
Ra b c d Reafc Rb e d f) = 0,
which is also true for the membranes discussed below, but not in general.
It is interesting to note that if the structure of the invariants are any indication, the
torus is a far more complicated object geometrically than the black hole.
For D = 4 through 7, the Kretschmann Invariant of the Kerr metric has but 4 or 5 terms, while for the
torus the number of terms grows from 31 to 4896 over the same range of dimensions!
Nonzero Cosmological Constant
Kerr solutions with nonzero cosmological constant
[Stuchlik]
exist in any dimension. Let
ρ2 = r2 + a2
cos2 (θ)
Δ(D) = (1 - 2 Λ r2 / ((D - 1) (D - 2)))
(r2 + a2) - μ / rD-5
ψ(D) = 1 + 2 a2 Λ
cos2 (θ) / ((D - 1) (D - 2))
Σ(D) = 1 + 2 a2 Λ / ((D - 1) (D - 2))
Then the metric in D dimensions is
ds2 = r2 cos2 (θ) dΩ2 +
ρ2 dr2 / Δ(D) +
ρ2 dθ2 /
ψ(D) +
(ψ(D) (r2 + a2)2 - Δ(D)
a2 sin2 (θ))
sin2 (θ)
dφ2 / (Σ2(D)
ρ2) +
2 a sin2 (θ) (ψ(D) (r2 + a2) -
Δ(D))
dφ dt / (Σ2(D)
ρ2) -
(Δ(D) - a2 ψ(D)
sin2 (θ)) dt2 / (Σ2(D)
ρ2)
This metric is an Einstein Manifold.
The invariants
R
Ra b Ra b
Ra b c d Ra b c d
Ra b Rca Rb c
Ra b c d Ra c Rb d
Ra b; c Ra b; c
Ra b; c Ra c; b
Ra b; a Rcb; c and
Ra b c d; a Reb c d; e
are all a simple sum of the corresponding invariants for
(A)dSD and the Kerr solution with
Λ = 0 (of course, the last four are identically zero).
For the other invariants of interest we find
Ra b c d Rea Rb c d e =
that for (A)dSD +
Λ
Ra b c d Ra b c d (Λ=0) / (D - 2)
Ra b c d Re fa b Rc d e f =
that for (A)dSD + that for KerrD(Λ=0) +
12 Λ
Ra b c d Ra b c d (Λ=0) / ((D - 1) (D - 2))
Ra b c d Reafc Rb e d f =
that for (A)dSD + that for KerrD(Λ=0) -
3 Λ
Ra b c d Ra b c d (Λ=0) / ((D - 1) (D - 2))
Ra b c d Reafc Rb f d e =
that for (A)dSD + that for KerrD(Λ=0) -
6 Λ
Ra b c d Ra b c d (Λ=0) / ((D - 1) (D - 2))
Ra b c d; e Ra b c d; e =
that for KerrD(Λ=0)
(1 + Λ f(r, c, μ, a))
and
εa b c i ...
εe f gi ...
Rb c eh Rf g a h =
that for (A)dSD + that for KerrD(Λ=0)
Ra b c d; e Ra b c d; e has a simplified form for the Schwarzschild solution:
Ra b c d; e Ra b c d; e = - 2 (D + 1) (D - 1) (D - 2) (D - 3)
μ2 ((D - 1) (D - 2) (μ - rD - 3) / 2 +
Λ rD - 1) / r3 (D - 1)
The Euler class for D = 4 and D = 6 are
that for (A)dS4 + that for Kerr4(Λ=0)
and
that for (A)dS6 + that for Kerr6(Λ=0) +
12 εa b c i ...
εe f gi ...
Rb c eh Rf g a h (Λ=0) / 5
respectively. The particularly simple forms which these invariants take is suggestive of
the difference in geometry engendered by the cosmological constant. These forms were most easily
found using the following Mathematica function:
Collect[Expand[#], lambda, simpler]&
The nonzero components of the first Pontrjagin Class
for the Kerr metrics are
| D | P1r c φ t |
|---|
| 4 | (- 9 a c μ2
r (a2 c2 - 3 r2) (3 a2 c2 - r2)) /
(4 (3 + a2 Λ)2 π2
(a2 c2 + r2)5) |
| 5 | (72 a c μ2 (a c - r) r (a c + r)) /
((6 + a2 Λ)2 π2
(a2 c2 + r2)5) |
| 6 | (- 25 a c μ2
(a2 c2 + 5 r2) (a4 c4 -
a2 c2 r2 + 10 r4)) / (3 (10 + a2
Λ)2 π2 r5
(a2 c2 + r2)5) |
| 7 | (- 225 a c μ2
(a2 c2 + 3 r2) (a4 c4 +
2 a2 c2 r2 + 5 r4)) / |
|
(2 (15 + a2
Λ)2 π2 r7
(a2 c2 + r2)5) |
| 8 | (- 441 a c μ2
(3 a2 c2 + 7 r2) (2 a4 c4 +
5 a2 c2 r2 + 7 r4)) / |
|
(4 (21 + a2
Λ)2 π2 r9
(a2 c2 + r2)5) |
| 9 | (- 1568 a c μ2
(a2 c2 + 2 r2) (5 a4 c4 +
13 a2 c2 r2 + 14 r4)) / |
|
(3 (28 + a2
Λ)2 π2 r11
(a2 c2 + r2)5) |
| 10 | (- 324 a c μ2
(5 a2 c2 + 9 r2) (5 a4 c4 +
13 a2 c2 r2 + 12 r4)) / |
|
((36 + a2
Λ)2 π2 r13
(a2 c2 + r2)5) |
| 11 | (- 2025 a c μ2
(3 a2 c2 + 5 r2) (7 a4 c4 +
18 a2 c2 r2 + 15 r4)) / |
|
(2 (45 + a2
Λ)2 π2 r15
(a2 c2 + r2)5) |
Note that all are proportional to both M and J, and vanish both on the equatorial hyperplane and in the
Schwarzschild limit.
Schwarzschild/Anti-deSitter in D=4
An interesting question arises when considering a black hole in an anti-deSitter background. We take D=4, a=0 and e=0 for simplicity.
Λ for this background can be written as -1/LAdS2, where LAdS is the anti-deSitter
length scale. The metric is then
ds2 = dr2 / (1 - 2 M / r + (r / LAdS)2 / 3) + r2 dθ2 +
r2 sin2 θ - dt2 (1 - 2 M / r + (r / LAdS)2 / 3),
and the asymptotically flat Schwarzschild solution is obtained in the limit LAdS→∞.
The scalar curvature for this metric is -4/LAdS: spacelike hypersurfaces have constant negative curvature, which means that
the neighborhood of every point is a "3-dimensional saddle". LAdS determines the relative size of those saddles.
For a spacelike hypersurface, the volume element is
r2 sin θ / √(1 - 2 M / r + (r / LAdS)2 / 3),
so the volume grows more slowly with r when LAdS is finite, and goes to zero as LAdS→0. Setting η=LAdS/M,
the horizon is located at
rhor = η2/3 (η2/3 - (√(η2 + 9) - 3) M / (√(η2 + 9) - 3)1/3
so that when:
- LAdS = 3 M / 2, rhor = LAdS;
- LAdS < 3 M / 2, rhor > LAdS;
- LAdS > 3 M / 2, rhor < LAdS.
Nothing in the equations of motion prohibit the first two possibilities, but what does it mean physically to suggest that the AdS length
scale is smaller than the black hole horizon? Small values of LAdS imply that space is highly curved over short distances;
how does this affect, for instance, geodesic motion?
Denoting the timelike Killing vector as ξ, the energy as measured by an observer with 4-velocity u is
E = - gμ ν ξμ uν
= (1 - 2 M / r + (r / LAdS)2 / 3) dt / dτ
and is of course a constant of the motion (τ is the proper time). We see that the vacuum energy increases the energy measured by the observer,
more for small LAdS.
There is a second constant of the motion associated with the azimuthal Killing vector:
the angular momentum
L = r2 dφ / dτ.
If we consider the null geodesic equations in the equatorial plane (which of course is perfectly general for a spherical system), we
can divide the equations for r(τ) and φ(τ) to obtain
dr / dφ = √(r (2M - r + (E2 / L2 - 1 / (3 LAdS2)) r3).
Writing L in terms of the apparent impact parameter b (as seen by a distant observer; see Wald, section 6.3), we have
dr / dφ = √(r (2M - r + (1 / b2 - 1 / (3 LAdS2)) r3).
The effect of finite LAdS is to increase the effective value of the impact parameter; light rays do not appear to be bent as much as they "should" be
by the black hole.
To find the distance of closest approach, we require dr/dφ=0 and
d2r / dφ2 = M - r + 2 r3 (1 / b2 - 1 / (3 LAdS2)) > 0.
Using the Mathematica function Reduce to find conditions for such solutions, we find
b < √3 LAdS
b > 3√3 M LAdS / √(LAdS2 + 9 M2)
rclosest = the real root of the polynomial equation
-6 M b2 LAdS2 + 3 b2 LAdS2 x +
(b2 - 3 LAdS2) x3 = 0
Because the effective potential has not been modified by LAdS, the location of the
potential barrier (and closest unstable circular orbit) has not changed; the root of the polynomial remains 3M.
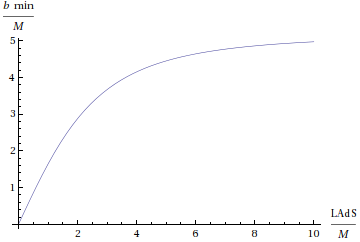
But the minimum apparent impact parameter below which light rays are captured by the black hole decreases with LAdS:
So as LAdS → 0, light rays can appear to come arbitrarily close to the center of the horizon without falling in, even though they
never get closer than 3M; the intense curvature allows them to bend completely around the black hole and appear to come out the other side. As
LAdS goes to ∞, the closest apparent impact parameter approaches its value for the asymptotically flat Schwarzschild solution of
3√3.
The next section examines inhomogeneous collapsing dust.
©2013, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.