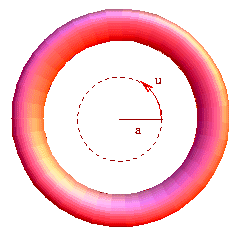

The round torus metric is most easily constructed via its embedding in a Euclidean space of one higher dimension. As with the sphere, this is not necessary for its definition: intrinsically, Tn is defined as a tensor product of n circles.
Let us begin with T2 embedded in R3. If a is the distance from the center of the hole to the center of the tube of the torus, and b (< a) is the radius of the tube:


then the torus is described by
(a - (x2 + y2)1/2)2 + z2 = b2.This can be parameterized by
x = cos(u)(a - b cos(v)),where the polar coordinate ρ = a - b cos(v) and u and v run from 0 to 2 π. Transforming to the intrinsic coordinate chart, we havey = sin(u)(a - b cos(v)) and
z = b sin(v).
gij = δk l dxk / dui dxl / dujand obtain the metric
ds2 = (a - b cos(v))2 du2 + b2 dv2.For T3 embedded in R4, we have
(b - ((a - (x2 + y2)1/2)2 + z2)1/2)2 + z22 = c2with parameterization
x = cos(u) (a + cos(v)(-b + c cos(w))),which yields the metricy = sin(u) (a + cos(v)(-b + c cos(w))),
z = sin(v) (b - c cos(w)) and
z2 = c sin(w),
ds2 = (a + cos(v)(-b + c cos(w)))2 du2 + (b - c cos(w))2 dv2 + c2 dw2.Note that b > c and a > b + c in order to avoid degeneracy singularities.
T4 embedded in R5 proceeds in exactly the same fashion, with embedding
(c - ((b - ((a - (x2 + y2)1/2)2 + z2)1/2)2 + z22)1/2)2 + z32 = d2and parameterization
x = cos(u) (a - cos(v) (b + cos(w) (-c + d cos(q)))),yielding the metricy = sin(u) (a - cos(v) (b + cos(w) (-c + d cos(q)))),
z = sin(v) (b + cos(w) (-c + d cos(q))),
z2 = sin(w) (c - d cos(q)) and
z3 = d sin(q)
ds2 = (a - cos(v) (b + cos(w) (-c + d cos(q))))2 du2 + (b - cos(w) (c - d cos(q)))2 dv2 +Once again, c > d, b > c + d and a > b + c + d in order to avoid degeneracy singularities.(c - d cos(q))2 dw2 + d2 dq2.
We can use the following Mathematica code to generate and verify a metric for Tn:
xu = Table[Symbol["t" <> ToString[i]], {i, dim}];Notice that we include code to verify that the metric satisfies the embedding equations. When constructing metrics in this fashion, it is always a good idea to make sure that the code always works. It is all too easy to generalize an algorithm which works fine for small dimensions and in the process introduce bugs which only show up when the dimension is large.rads = {ra, rb, rc, rd, re, rf, rg, rh, ri, rj, rk};
xcu = {rads[[dim]] Sin[xu[[dim]]]};
Do[
PrependTo[xcu, Simplify[ Sin[xu[[j]]] (rads[[j]] - xcu[[1]] Cot[xu[[j + 1]]])]],PrependTo[ xcu, Cot[xu[[1]]] xcu[[1]]];{j, dim - 1, 1, -1}];
chk = xcu[[1]]^2;
Do[
chk = simpler[ Simplify[ (rads[[j - 1]] - Sqrt[chk + xcu[[j]]^2])^2]],Print[ "Check: ", simpler[ Simplify[ chk]]];{j, 2, dim + 1}];
gll = simpler[ Simplify[ Table[ Table[ simpler[ Simplify[
Sum[ D[xcu[[k]], xu[[i]]] D[xcu[[k]], xu[[j]]], {k, dim + 1}]]],{j, dim}], {i, dim}]]];
After transforming from angular to cosine coordinates, we have for n = 2:
ds2 = (ra - c2 rb)2 dc12 +for n = 3:rb2 / (1 - c22) dc22
ds2 = (ra - c2 rb + c2 c3 rc)2 dc12 +and for n = 4:(rb - c3 rc)2 / (1 - c22) dc22 +rc2 / (1 - c32) dc32
ds2 = (ra - c2 rb + c2 c3 rc - c2 c3 c4 rd)2 dc12 +Note that in each case we have introduced coordinate singularities at ci > 1 = +- 1. These can be covered by translation of the original angle.(rb - c3 rc + c3 c4 rd)2 / (1 - c22) dc22 +(rc - c4 rd)2 / (1 - c32) dc32 +
rd2 / (1 - c42) dc42
The nonzero Christoffel Symbols for n = 2, 3 and 4 are
| n = 2 | n = 3 | n = 4 | |
| Γ11 2 | rb / (- ra + c2 rb) | (rb - c3 rc) / | (rb - c3 rc + c3 c4 rd) / |
| (- ra + c2 rb - c2 c3 rc) | (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd) | ||
| Γ11 3 | c2 rc / (ra - c2 rb + c2 c3 rc) | c2 (rc - c4 rd) / | |
| (ra - c2 rb + c2 c3 rc - c2 c3 c4 rd) | |||
| Γ11 4 | c2 c3 rd / (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd) | ||
| Γ21 1 | - (1 - c22) (- ra + c2 rb) / | - (1 - c22) (- ra + c2 rb - c2 c3 rc) / | - (1 - c22) (- ra + c2 rb - c2 c3 rc + |
| rb | (rb - c3 rc) | c2 c3 c4 rd) / (rb - c3 rc + c3 c4 rd) | |
| Γ22 2 | c2 / (1 - c22) | c2 / (1 - c22) | c2 / (1 - c22) |
| Γ22 3 | rc / (- rb + c3 rc) | (rc - c4 rd) / (- rb + c3 rc - c3 c4 rd) | |
| Γ22 4 | c3 rd / (rb - c3 rc + c3 c4 rd) | ||
| Γ31 1 | - c2 (1 - c32) (ra - c2 rb + c2 c3 rc) / | - c2 (1 - c32) (ra - c2 rb + c2 c3 rc - | |
| rc | c2 c3 c4 rd) / (rc - c4 rd) | ||
| Γ32 2 | - (1 - c32) (- rb + c3 rc) / | - (1 - c32) (- rb + c3 rc - c3 c4 rd) / | |
| ((1 - c22) rc) | ((1 - c22) (rc - c4 rd)) | ||
| Γ33 3 | c3 / (1 - c32) | c3 / (1 - c32) | |
| Γ33 4 | rd / (- rc + c4 rd) | ||
| Γ41 1 | - c2 c3 (1 - c42) (- ra + c2 rb - c2 c3 rc + | ||
| c2 c3 c4 rd) / rd | |||
| Γ42 2 | - c3 (1 - c42) (rb - c3 rc + c3 c4 rd) / | ||
| ((1 - c22) rd) | |||
| Γ43 3 | - (1 - c42) (- rc + c4 rd) / ((1 - c32) rd) | ||
| Γ44 4 | c4 / (1 - c42) |
Naively, we see that the cn direction is geodesic, and there are n - 2 geodesic hypersurfaces defined by {ci ... cn} for i from 2 to n - 1. But note that for specific values of ci, other directions are geodesic as well. In general, ci is a geodesic direction when ci+1 through cn are equal to +-1. But since the origin of the ci can be translated by a constant without changing the Christoffel Symbols, we see that in fact every direction is a geodesic direction. This is of course consistent with the topology of the torus as a tensor product of circles, and indicates that the business of analyzing the Christoffel Symbols for geodesic behavior is a mildly dangerous one, since they are not invariant with respect to diffeomorphisms.
For the same reason, the components of the Riemann and Ricci Tensors are less useful than the invariants which we are examining for the purpose of building geometric intuition. We will nonetheless continue to present them in "natural coordinates" for the sake of completeness, and in order to allow students to check their work. The nonzero components of the Riemann Tensor for n = 2, 3 and 4 are
| n = 2 | n = 3 | n = 4 | |
| R1 2 1 2 | c2 rb (- ra + c2 rb) / | c2 c32 (- rb + c3 rc) * | c2 c32 c42 (rb - c3 rc + c3 c4 rd) * |
| (1 - c22) | (ra - c2 rb + c2 c3 rc) / (1 - c22) | (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd) / (1 - c22) | |
| R1 3 1 3 | c2 c3 rc (ra - c2 rb + c2 c3 rc) / | c2 c3 c42 (- rc + c4 rd) * | |
| (1 - c32) | (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd) / (1 - c32) | ||
| R1 4 1 4 | c2 c3 c4 rd (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd) / (1 - c42) | ||
| R2 3 2 3 | c3 rc (- rb + c3 rc) / | c3 c42 (- rc + c4 rd) (rb - c3 rc + c3 c4 rd) / | |
| ((1 - c22) (1 - c32)) | ((1 - c22) (1 - c32)) | ||
| R2 4 2 4 | c3 c4 rd (rb - c3 rc + c3 c4 rd) / ((1 - c22) (1 - c42)) | ||
| R3 4 3 4 | c4 rd (- rc + c4 rd) / ((1 - c32) (1 - c42)) |
The nonzero components of the Ricci Tensor for n = 2, 3 and 4 are
| n = 2 | n = 3 | n = 4 | |
| R1 1 | c2 (- ra + c2 rb) / rb | c2 c3 (- rb + 2 c3 rc) (ra - c2 rb + c2 c3 rc) / (rc (- rb + c3 rc)) | c2 c3 c4 (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd) (- rb rc + c3 rc2 + 2 c4 rb rd - 4 c3 c4 rc rd + 3 c3 c42 rd2) / (rd (- rc + c4 rd) (rb - c3 rc + c3 c4 rd)) |
| R2 2 | c2 rb / ((1 - c22) (- ra + c2 rb)) | c3 (- rb + c3 rc) (ra - c2 rb + 2 c2 c3 rc) / ((1 - c22) rc (ra - c2 rb + c2 c3 rc)) | c3 c4 (rb - c3 rc + c3 c4 rd) (ra rc - c2 rb rc + c2 c3 rc2 - 2 c4 ra rd + 2 c2 c4 rb rd - 4 c2 c3 c4 rc rd + 3 c2 c3 c42 rd2) / ((1 - c22) rd (- rc + c4 rd) (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd)) |
| R3 3 | c3 rc (ra - 2 c2 rb + 2 c2 c3 rc) / ((1 - c32) (- rb + c3 rc) (ra - c2 rb + c2 c3 rc)) | c4 (- rc + c4 rd) (- (ra rb) + c2 rb2 + c3 ra rc - 2 c2 c3 rb rc + c2 c32 rc2 - 2 c3 c4 ra rd + 4 c2 c3 c4 rb rd - 4 c2 c32 c4 rc rd + 3 c2 c32 c42 rd2) / ((1 - c32) rd (rb - c3 rc + c3 c4 rd) (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd)) | |
| R4 4 | c4 rd (- (ra rb) + c2 rb2 + 2 c3 ra rc - 4 c2 c3 rb rc + 3 c2 c32 rc2 - 2 c3 c4 ra rd + 4 c2 c3 c4 rb rd - 6 c2 c32 c4 rc rd + 3 c2 c32 c42 rd2) / ((1 - c42) (- rc + c4 rd) (rb - c3 rc + c3 c4 rd) (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd)) |
The invariants we have chosen to examine, for n = 2 and 3, are
| R | 2 c2 / | 2 c3 (ra - 2 c2 rb + 3 c2 c3 rc) / |
| (rb (- ra + c2 rb)) | (rc (- rb + c3 rc) (ra - c2 rb + c2 c3 rc)) | |
| Ra b Ra b | 2 c22 / | (2 c32 (ra2 - 3 c2 ra rb + 3 c22 rb2 + 4 c2 c3 ra rc - 8 c22 c3 rb rc + 6 c22 c32 rc2)) / |
| (rb2 (- ra + c2 rb)2) | (rc2 (- rb + c3 rc)2 (ra - c2 rb + c2 c3 rc)2) | |
| Ra b c d Ra b c d | 4 c22 / | (4 c32 (ra2 - 2 c2 ra rb + 2 c22 rb2 + 2 c2 c3 ra rc - 4 c22 c3 rb rc + 3 c22 c32 rc2)) / |
| (rb2 (- ra + c2 rb)2) | (rc2 (- rb + c3 rc)2 (ra - c2 rb + c2 c3 rc)2) | |
| Ra b Rca Rb c | 2 c23 / | (c33 (2 ra3 - 9 c2 ra2 rb + 15 c22 ra rb2 - 10 c23 rb3 + 12 c2 c3 ra2 rc - 36 c22 c3 ra rb rc + 36 c23 c3 rb2 rc + 24 c22 c32 ra rc2 - 48 c23 c32 rb rc2 + 24 c23 c33 rc3)) / |
| (rb3 (- ra + c2 rb)3) | (rc3 (- rb + c3 rc)3 (ra - c2 rb + c2 c3 rc)3) | |
| Ra b c d Ra c Rb d | 2 c23 / | (2 c33 (ra3 - 4 c2 ra2 rb + 6 c22 ra rb2 - 4 c23 rb3 + 5 c2 c3 ra2 rc - 17 c22 c3 ra rb rc + 17 c23 c3 rb2 rc + 12 c22 c32 ra rc2 - 24 c23 c32 rb rc2 + 12 c23 c33 rc3)) / |
| (rb3 (- ra + c2 rb)3) | (rc3 (- rb + c3 rc)3 (ra - c2 rb + c2 c3 rc)3) | |
| Ra b c d Rea Rb c d e | 2 c23 / | (c33 (2 ra3 - 7 c2 ra2 rb + 9 c22 ra rb2 - 6 c23 rb3 + 8 c2 c3 ra2 rc - 20 c22 c3 ra rb rc + 20 c23 c3 rb2 rc + 12 c22 c32 ra rc2 - 24 c23 c32 rb rc2 + 12 c23 c33 rc3)) / |
| (rb3 (- ra + c2 rb)3) | (rc3 (- rb + c3 rc)3 (ra - c2 rb + c2 c3 rc)3) | |
| Ra b c d Re fa b Rc d e f | 8 c23 / | (8 c33 (ra3 - 3 c2 ra2 rb + 3 c22 ra rb2 - 2 c23 rb3 + 3 c2 c3 ra2 rc - 6 c22 c3 ra rb rc + 6 c23 c3 rb2 rc + 3 c22 c32 ra rc2 - 6 c23 c32 rb rc2 + 3 c23 c33 rc3)) / |
| (rb3 (- ra + c2 rb)3) | (rc3 (- rb + c3 rc)3 (ra - c2 rb + c2 c3 rc)3) | |
| Ra b c d Reafc Rb e d f | 0 | (6 c22 c34) / |
| (rc2 (- rb + c3 rc)2 (ra - c2 rb + c2 c3 rc)2) | ||
| Ra b c d Reafc Rb f d e | - 2 c23 / | (- 2 c33 (ra2 - c2 ra rb + c22 rb2) (ra - 2 c2 rb + 3 c2 c3 rc)) / |
| (rb3 (- ra + c2 rb)3) | (rc3 (- rb + c3 rc)3 (ra - c2 rb + c2 c3 rc)3) | |
| Ra b; c Ra b; c | 2 (1 - c22) ra2 / | |
| (rb4 (- ra + c2 rb)4) | ||
| Ra b; c Ra c; b | (1 - c22) ra2 / | |
| (rb4 (- ra + c2 rb)4)) | ||
| Ra b; a Rcb; c | (1 - c22) ra2 / | |
| (rb4 (- ra + c2 rb)4)) | ||
| Ra b c d; e Ra b c d; e | 4 (1 - c22) ra2 / | |
| (rb4 (- ra + c2 rb)4) | ||
| Ra b c d; a Reb c d; e | 2 (1 - c22) ra2 / | |
| (rb4 (- ra + c2 rb)4) | ||
| εa b c i ... εe f gi ... Rb c eh Rf g a h | (- 8 c2 c32 (- (ra rb) + c2 rb2 + 2 c3 ra rc - 4 c2 c3 rb rc + 3 c2 c32 rc2)) / | |
| (rc2 (- rb + c3 rc)2 (ra - c2 rb + c2 c3 rc)2) |
Eulern = 4 = (3 c2 c32 c43) / (4 π2 rd (- rc + c4 rd) (rb - c3 rc + c3 c4 rd) (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd))
Eulern = 6 = (15 c2 c32 c43 c54 c65) / (8 π3 rf (- re + c6 rf) (rd - c5 re + c5 c6 rf) (- rc + c4 rd - c4 c5 re + c4 c5 c6 rf) (rb - c3 rc + c3 c4 rd - c3 c4 c5 re + c3 c4 c5 c6 rf) (- ra + c2 rb - c2 c3 rc + c2 c3 c4 rd - c2 c3 c4 c5 re + c2 c3 c4 c5 c6 rf))
Note the simlilarity among the invariants for T2, and the corresponding lack of simliarity for T3. In general, the complexity of the results make them rather useless for larger dimension. For instance, for the Kretschmann Invariant, there are 31 terms for n = 4, 163 terms for n = 5, 882 terms for n = 6 and 4896 terms for n = 7. It is interesting to note that for all invariants we computed, the denominator is equal to a power of the numerator of the determinant of the metric. Hence all are regular. The zeroes obviously have no invariant meaning since they can be removed by simple translation of the angular coordinates.
The next section explores cosmological solutions to Einstein's Equations.
©2005, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.