(prev)

(top)

(next)

Electrical Potential

1. Electric charge is quantized in units of e = 1.60218 * 10^-19 Coulombs. (C): q = n e.

   Electric charge is the source of the electric field. A field is a smooth function which has a value at every point in space. The value may be a scalar or a vector.

2. The (scalar) electric potential field due to a distribution of electric charges is

   V(x,y,z) = (1 / (4 π ε)) ∫ dq / r

   where the integral is a sum over all of the charges and the denominator of the integrand is the distance from each bit of charge to the field point (x,y,z).

   Assuming a uniform medium, ε is the electrical permittivity, often written as

   ε ≡ κ ε₀,

   where κ is the dielectric constant (≥ 1) and ε₀ is the permittivity of the vacuum, equal to 8.8542 * 10^-12 C² / (N m²). The permittivity is a measure of how "effective" the field is in the medium.

   V is measured in Volts; 1 V = 1 J / C, so the electrical potential energy of a charge at a point in space is

   U = q_t V

   where q_t is the test charge: an artifice used to measure the field without contributing to it. Think of the electric potential as the potential energy per unit charge at every point in space.

   This applet will allow you to experiment with the potentials due to various charge configurations.

3. We often define uniform volume, surface and linear charge densities:

   ρ ≡ Q / V,
   σ ≡ Q / A, or
   λ ≡ Q / L,

   so that in the integrals for the field:

   dq = ρ dV,
   dq = σ dA, or
   dq = λ dL.

   Note that dl, dA and dV are implicitly positive; when expressing them in terms of coordinates, pay close attention to integration limits! Check yourself by noting that V should have the same sign as the charge density involved.

   Consider a wire of length b, with constant linear charge density λ, extending from the origin at an angle θ:

   

   Choosing the field point to be (x, y), and calling the distance from the origin to the source point (along the wire) "s", we have

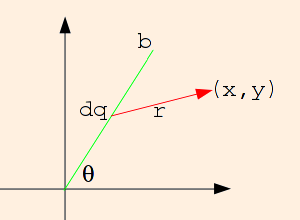
   r = (x - s cos θ, y - s sin θ)

   r = √ (s² + x² + y² - 2 s (x cos θ + y sin θ))

   Since s is manifestly positive, dq is equal to λ ds. So

   V(x, y) = (1 / (4 π ε)) ∫₀^b λ ds / √ (s² + x² + y² - 2 s (x cos θ + y sin θ)).

   Substituting

   u = s - (x cos θ + y sin θ)

   = s - a

   will put this integral into a simpler form (since the quantity in parentheses is a constant with respect to the integration variable, we have chosen to call it "a"). Since ds = du, integrating gives us

   V(x, y) = (1 / (4 π ε)) ∫_{- a}^{b - a} λ du / √ (u² + x² + y² - a²)

   = (λ / (4 π ε)) ln (u + √ (u² + x² + y² - a²) |_{- a}^{b - a}

   = (λ / (4 π ε)) ln ((b - a + √ (b² + x² + y² - 2 b a)) / (√ (x² + y²) - a))

   (Note that this derivation fails if the field point is collinear with the wire; but of course, that is an easy special case to do "by hand"!)

   We can easily compute the potential due to a line of charge extending from (-b,0) to (b,0) as

   V(x,y) | θ=0 + V(x,y) | θ=π

   = V(x,y) | a=x + V(x,y) | a=-x

   = (λ / (4 π ε)) (ln ((b - x + √ ((b - x)² + y²)) / (√ (x² + y²) - x)) +

   ln ((b + x + √ ((b + x)² + y²)) / (√ (x² + y²) + x)))

   = (λ / (4 π ε)) ln ((b - x + √ ((b - x)² + y²))(b + x + √ ((b + x)² + y²)) / y²).

   If the field point is on the y axis, this becomes

   (λ / (2 π ε)) ln ((b + √ (b² + y²)) / y).

4. A conductor has freely mobile valence electrons. In any charged conductor, the valence electrons will distribute themselves equidistantly on the surface so as to minimize their potential energies. This makes the conductor an equipotential volume.

(prev)

(top)

(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.