
When you pet your cat on a dry day, the fur will rise to meet your hand, defying gravity in the name of "static electricity". We explain this behavior by saying that there was a transfer of electric charge from the cat's fur to your hand: negative charge has been rubbed off on to your hand, leaving the cat positively charged. The fur is then attracted to your negatively charged hand. While the assignment of the words negative and positive are purely conventional, the fact remains that charge comes in two types. Charges with the same sign repel each other and charges with the opposite sign are attracted to each other.
The sizes of these charges are measured in Coulombs (abbreviated C), which is a new fundamental unit for us.
While the cat and your hand are certainly macroscopic objects, physicists have identified the two objects which account for the vast majority of freely moving electrical charge in the universe as microscopic electrons and protons. For the present, we will simply consider them as VERY small point-like particles: the electron is negative (by convention) and the proton is positive. The mass of the electron is 9.109 * 10-31 kg, the mass of the proton is 1.673 * 10 -27 kg, and the magnitude of their electrical charge is
But all this presents a fundamental problem to our intuition. With the notable exception of gravity, the forces and pressures we have studied have been communicated by physical contact. How can the electric and gravitational forces act at a distance, without direct contact?
We can construct a model of this simple phenomenon using one of the most universally applicable ideas in physics: action at a distance is caused by the interaction of a test charge with the potential field created by a source charge. The source charge is imagined to be glued in place. The field which it creates has a value at every point in space. In a fictional scenario which allows us to measure the field due to a single charge, we pretend that the test charge DOES NOT AFFECT the field created by the source. Since any two charges will either attract or repel each other, the placement of a test charge in the field of a source means that the test charge has a nonzero potential energy. The value of the field at any point in space is the energy per unit charge that the test charge has due to the presence of the source.
The electrical potential at a distance r from a source charge q is
In the equation for V, r as the argument of the function V specifies a location (the field point) where we want to compute the field; this is the location of the test charge. Since the only coordinate V depends on is r, we say that V has spherical symmetry. This is due to the use of a dimensionless point to represent the source of the field. Around such a point, all directions are equivalent, and so the field can only depend on the radial distance from the point.
V has SI units of J / C (also denoted by V for Volts), and the energy of a test charge in the presence of V is called its electrical potential energy:
As was the case with the gravitational potential energy, measurement of the electric potential is relative. As you might guess from the units, electric potential can be measured with an ordinary voltmeter. But the value of the measurement is the potential difference between the two probes. We commonly designate the potential of the Earth's surface as zero (in analogy to the gravitational potential) and measure V relative to "ground".
The potential field at a point due to a collection of source charges is equal to the sum of the fields due to the individual charges, at that point:
Similarly, the energy of a test charge in the presence of such a field is simply the sum of its energies relative to each of the source charges. We say that the fields superpose, and that the sum field is the superposition of the fields due to the individual sources.
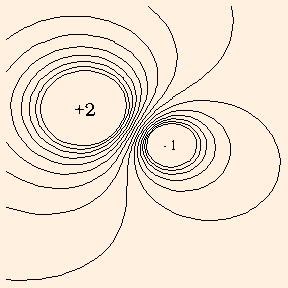
If we were to plot the electrical potential field due to a pair of source charges, we would see that there are lines, called equipotentials, on which the electrical potential has the same value everywhere:
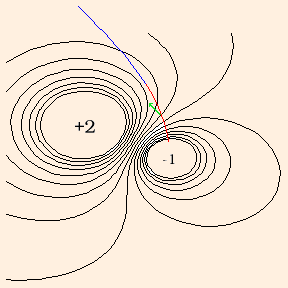
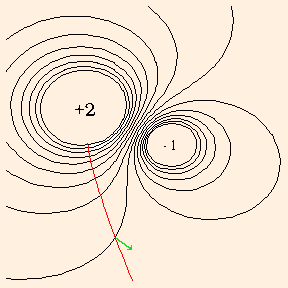
The potential is analogous to temperature: there is a different temperature at every point in space, and the temperature gradients tell you where heat flows. At any point, the gradient is the direction the field changes most quickly; this direction is of course perpendicular to the lines where the field is constant. Hence heat flows perpendicularly to isothermals, and charges move perpendicularly to equipotentials. Since charges move in the direction of least energy a test particle will accelerate along the gradient toward a charge or charges of the opposite sign:
Here the red and blue line represents the motion of a negative test charge, with the velocity always tangent to the trajectory. The line is colored red while the speed is increasing, and blue as it slows under the influence of the positive source charge. The acceleration is always perpendicular to the equipotentials; the buildup of momentum causes the trajectory to deviate from the acceleration at any point. The acceleration at one equipotential is drawn in green. The following graph represents the motion of a positive test charge:
The gravitational potential field is exactly analogous to the electrical potential field, with mass replacing charge as the source of the field:
The most significant differences between the electric and gravitational fields is that the gravitational sources are always positive, and the constant of proportionality is much smaller, indicating that the gravitational field is much weaker.
The following applet will give you some exercise with potential fields. It will work with both electrical and gravitational fields; if the problem is specified as an electrical problem, charges will be measured in units of e and distances will be measured in Angstroms (1 A = 10-10 m), and if the problem is a gravitational one, masses will be measured in Solar masses (1 MS = 2 * 1030 kg) and distances will be measured in Astronomical Units (1 AU = 1.5 * 1011 m). Each grid square is one distance unit: coordinates range from (-3,-3) to (3,3).
Click on the grid to place your charges (or masses), and specify their values by clicking on the source buttons. By pushing the potential button, you will cause the applet to draw a color temperature plot of the potential. In this plot, positive values increase from black to red to orange to yellow, and negative values decrease from black to green to cyan (light blue). Equipotentials are therefore lines which border different colors. Pushing the grid button will remove the color plot so that the coordinates of the charges can be clearly seen. After specifying a test charge location and value, you will be asked for the magnitude of the potential or energy, and for the direction of the acceleration of the test charge.
As you do these problems, try some symmetrical source charge configurations: sets of charges which are symmetric with respect to reflection about some line. A test charge which starts on a line of symmetry will stay on that line forever as it accelerates. Can you see why this must be so? Also try some lattices: regular, alternating positive and negative source charges make a good model of an ionic crystal.
What meaning can we assign to the concept of negative potential energy?
When U = m g h, the meaning is clear: the y coordinate is simply negative in the coordinate system we have chosen. Since
in these situations, y=0 is generally chosen to be at the Earth's surface at some location, a negative value of y, and hence of U, simply
means we are in a hole in the ground.
In the more general cases of electrical or gravitational potential energy,
U represents the amount of energy that needs to be expended to bring the test charge or mass to the field point from
infinity, which is usually where the potential is taken to be zero (since as r tends to infinity, U tends to zero).
Hence a negative electrical potential energy implies that the test charge "wants" to be at the field point: not only does it
not take an expenditure of energy to get it there, it takes an expenditure of energy to keep it away!
In general, a test particle whose potential energy is negative is bound to the source(s).
The next section explains how the potential field gives rise to forces.
©2008, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
e = 1.6 * 10-19 C.
All free electric charge appears to be quantized in units of e; free charges less than e have never been observed, and all charges are integer multiples of e:
q = n e.
Why this is so, and why e has the value it has, are two of the fundamental mysteries of the universe; and two of the most interesting problems in physics! Because the unit of charge is so small, the charge lost by your cat was a LARGE number of electrons. The typical charge on your cat might be 10-9 C, indicating a deficit on the order of 1010 electrons. By contrast, the charge in the average lightning stroke is around 30 C.
Potential Fields
V(r) = q / 4 π ε r,
where ε (the Greek letter epsilon) is the electrical permittivity of the medium in which the field exists. ε is a measure of the effectiveness with which the electrical force is felt across the medium. It is often written as the product of κ and ε0, where ε 0 = 8.85 * 10-12 C2 / N m2 is the electrical permittivity of the vacuum, and κ is the dielectric constant of the medium (1 for the vacuum, 1.00059 for air, 80 for water at 20 degrees C). Note that for the vacuum, 1 / 4 π ε is approximately 9 * 109 N m2 / C2.
U = qt Vs,
where t indicates the test charge and s indicates the field (at the field point) due to the source.
Vq1 + q2 = q1 / 4 π ε r1 + q2 / 4 π ε r2,
where r1 is the distance from q1 to the field point, and r2 is the distance from q2 to the field point.
Equipotentials
Gravitational Fields
V(r) = - G M / r.
Here G is Newton's Constant, equal to 6.673 * 10-11 N m2 / kg2. The minus sign indicates that the potential always results in an attractive force; the gravitational potential energy of a test mass:
U = Mt Vs
is always negative, just as the electrical potential energy is negative for source and test charges of opposite sign, which feel an attractive force.