(prev)(top)(next)

Electrical Circuits

  1. Two resistors in series have the same current so with Ohm's law,
    ΔVeq = ΔV1 + ΔV2
    becomes
    Req = R1 + R2
    Two resistors in parallel have the same voltage drop so with Ohm's law,
    Ieq = I1 + I2
    becomes
    1/ Req = 1 / R1 + 1 / R2

  2. Conservation of charge gives Kirchhoff's junction rule: Σjunction I = 0.

    Conservation of energy gives Kirchhoff's loop rule: Σclosed loop ΔV = 0.

  3. In an RC circuit we have from the loop rule:
    V - q / C - I R = 0

    (q - C V) = - R C dq / dt

    dq / (q - C V) = - dt / (R C)

    ln (q - C V) = a - t / (R C)

    q(t) = C V + b e - t / (R C)

    If q(0) = 0 and V > 0 (charging),
    q(t) = C V (1 - e - t / (R C))
    If q(0) = Q and V = 0 (discharging),
    q(t) = Q e - t / (R C)
    The time constant is τ ≡ R * C.
    This plot shows the current (dq/dt) charging the capacitor in blue and the current through the resistor in red:
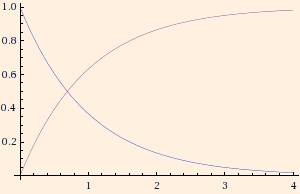
    Note that as the capacitor charges, the current shifts from it to the resistor. When the capacitor is fully charged, it is effectively open and all of the current flows through the resistor.

  4. This applet will allow you to practice analysis of some simple RC networks.

(prev)(top)(next)

©2012, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.