(prev)

(top)

(next)

Waves

1. Consider a string of mass per unit length μ and tension T. The y coordinate can be considered as a function of both x and t.

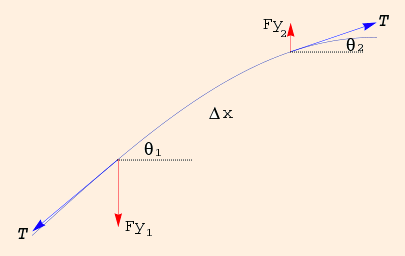
   For a segment of length Δx (almost horizontal, but blown up here for clarity):

   
   • F_y = T sin θ ≈ T tan θ = T Δy/Δx.
   • F = ma takes the form

     μ Δx d²y/dt² = F_y2 - F_y1

     = T ((Δy/Δx)|_{x + Δx} - (Δy/Δx)|_x)

     and in the limit Δx → 0:

     μ/T d²y/dt² = d²y/dx².

   This is called the wave equation. Note that it is linear: if y₁ and y₂ are both solutions, so is y₁ + y₂ (the superposition of the two solutions).
2. The general solution is

   y(x,t) = f(x - c t) + g(x + c t).

   These are "right-movers" and "left-movers", respectively. With u = x - c t:

   μ/T d²f(u)/dt² = d²f(u)/dx²

   μ/T (-c) df'(u)/dt = df'(u)/dx

   μ/T c² f''(u) = f''(u)

   Both "movers" have propagation (translation) velocity c = √(T/μ), so the wave equation has the general form

   d²y/dt² = c² d²y/dx².

3. Let f(x - c t) = A sin(k x - ω t + φ) (recall the simple harmonic oscillator). Then

   f(x - c t) = A sin(k (x - ω t / k) + φ)

   and

   c = ω / k.

4. From the periodicity of this function we see that k = 2 π / λ, where λ is the wavelength (the horizontal distance spanned by one cycle) and k is the wave number (the number of radians per unit length).

   The propagation velocity is then c = λ ν, where ν is the frequency.

   See this applet for how changes in wave number and phase angle affect a wave.

5. The preceding analysis of transverse waves on a string (where the direction of wave displacement is normal to the direction of wave propagation) is much more general than it appears. It applies to any linear wave motion in a medium which has attributes corresponding to inertia and tension; in particular, to linear waves in fluid media (ie., air or water), to longitudinal waves (where the wave displacement is parallel to the direction of wave propagation), and as we shall see, to linear electromagnetic waves in any medium.

   It does not, however, apply to nonlinear waves.

6. The power flowing through the point x is the product of the upward force (-T dy/dx) with the upward velocity (dy/dt). Integrating this at x = 0 over one period, and dividing by the period, gives the average power delivered per cycle:

   P = μ ω² A² c / 2.

(prev)

(top)

(next)

©2011, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.