(prev)

(top)

(next)

Diffraction

1. For 2 slit diffraction and gratings, constructive and destructive interference are determined by

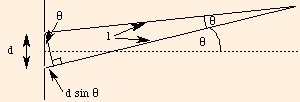
   Δpath length = d sin θ = m or (m + 1/2) λ,

   respectively, where d is the separation between slits (grating spacing), θ is measured from the normal to the slits and m is a non-negative integer:
   

   Note that since sin θ ≤ 1, m or (m + 1/2) must be ≤ d / λ.

2. These applets demonstrates diffraction.
3. For single slit diffraction, the intensity is

   I_single = I_max (sin(π a (sin θ) / λ) / (π a (sin θ) / λ))².

   This can only be solved numerically for constructive interference, but for destructive interference we find the path length

   Δpath length = a sin θ / (2 m),

   where a is the slit width and m is a nonzero integer. This is equivalent to dividing the slit into an even number of parts, each of which acts as a point source.

   For double slit diffraction, the intensity is I_single cos(π d (sin θ) / λ)², from which we retrieve the conditions above.

4. For diffraction in crystals, Δpath length = 2 d sin θ, where d is the lattice spacing. The factor of two comes from the fact that diffraction is taking place between two adjacent planes in the crystal.
5. The smallest angle of resolution (in radians) for a circular aperture is 1.22 λ / d, where d is the aperture diameter.

(prev)

(top)

(next)

©2010, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.