Notes for Calculus-based Physics

(prev) (top) (next)

Vectors

Except when velocities approach the speed of light, or in large gravitational fields, motions in any three perpendicular directions are completely independent.

A vector has one component for each independent direction of interest. In three dimensions,

V = (v_x, v_y, v_z)
= v_x i + v_y j + v_z k,

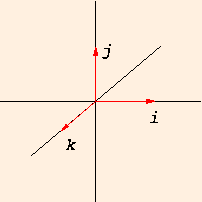
where i, j and k are unit vectors (of length 1) in the x, y and z directions, respectively. If i and j are in their usual positions in the plane of the page, the direction of k is out of the page, pointing towards you:

Position, velocity and acceleration are all vectors. We will denote vectors in red bold type in these notes.

The sum or difference of two vectors U and V is

U ± V = (u_x ± v_x, u_y ± v_y, u_z ± v_z).

It is often called the resultant.

The vector from the point u to the point v is v - u.

The inner product or dot product of two vectors U and V is

U ⋅ V ≡ u_x * v_x + u_y * v_y + u_z * v_z

Note that it is zero if U and V are perpendicular. Think of the dot product as the component of U along the direction of V, times the magnitude of V.

The length (or magnitude) of a vector V is

V ≡ |V| = √ (V ⋅ V).

V / V is the unit vector in the direction of V.

Note that the sum of vector magnitudes is in general meaningless.

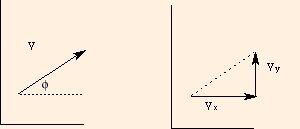
In two dimensions, using ordinary polar coordinates (φ measured counterclockwise from the positive x axis, 0 ≤ φ < 2π),
v_x = V cos φ, and
v_y = V sin φ.
Note that tan φ = v_y / v_x.
Note that these equations are only valid for φ measured counterclockwise from the positive x axis. If you label a different angle as φ, you may have v_x = V sin φ, etc.
In general, the length of a vector is the length of the hypotenuse of a right triangle whose sides are the vector components:

See this applet for examples.

When motion is on an inclined plane, resolve the relevant vectors into components parallel and normal to the plane:

The vector product or cross product of two vectors U and V is
U ⊗ V ≡ (U_y V_z - U_z V_y, U_z V_x - U_x V_z, U_x V_y - U_y V_x)
and is perpendicular to both U and V. This implies

i ⊗ j = k j ⊗ i = -k i ⊗ i = 0

j ⊗ k = i k ⊗ j = -i j ⊗ j = 0

k ⊗ i = j i ⊗ k = -j k ⊗ k = 0

Note that it is zero if U and V are (anti-)parallel. Think of the cross product as the component of U perpendicular to the direction of V, times the magnitude of V.

(prev) (top) (next)

©2010, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.