
It is often helpful for us to have a shorthand notation for quantities with both x and y coordinates. Since the x and y directions are perpendicular to each other, nothing that happens in the x direction has any effect on what happens in the y direction, and vise versa (ignoring for the moment the subject of magnetism). The x and y directions are mutually independent. This means that when we discuss the motion of an object in two dimensions, we need four independent equations instead of two, with eleven independent unknowns instead of six (x, x0, vx, vx0, ax , y, y0, vy, vy0, ay and t ):
x = x0 + vx0 t + ax t2 / 2,andvx = vx0 + ax t
y = y0 + vy0 t + ay t2 / 2,vy = vy0 + ay t.
The additional unknowns represent the doubling of the spatial degrees of freedom: from motion on a line (in the x direction only), we now have motion in a plane. Here, each of the x and y components of the initial velocity and the acceleration must be specified separately; hence the additional subscripts. Remember that in the above equations, the acceleration is still a constant; there are separate constant accelerations in the x and y directions.
The "vector" is a notation which enables us to capture the similarity of the above equations and write them as one. Here we define the vector "V":
V = (Vx, Vy).
The vector V is a pair of real numbers Vx and Vy, which are called the "x component" and "y component" of the vector. It indicates the direction and distance one would go by walking Vx in the x direction, and then walking Vy in the y direction (or vise versa; the order is unimportant):
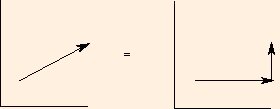
Note that we will encounter many vectors which represent quantities with a direction in space but whose magnitude has nothing to do with distance.
The position vector is a shorthand for the coordinates of an object:
X = (x, y).Likewise, an object which lives in two dimensions (ie., on the plane of a blackboard) also has a two dimensional velocity:
V = (vx, vy)and a two dimensional acceleration:
A = (ax, ay).In vector notation, the four equations for uniform accelerated motion become
X = X0 + V0 t + A t2 / 2and
V = V0 + A t.X0 and V0 are the initial position and velocity vectors, respectively. Note that these equations are isomorphic to the first two pairs of equations; each is really two equations in one. The x component of each equation is the first pair of the above four equations, and the y component of each equation is the second. Notice also that we have not lost any unknowns. Since each of the five vectors in these equations have two components, we still have eleven unknowns in four equations.
If we consider a cat jumping from a chair, we find that the components of the vectors necessary to compute its trajectory are
X0 = (0, h0),andV0 = (vx0, vy0)
A = (0, - g),where we take the origin to be under the cat, we must specify the x and y components of the initial velocity separately, and we ignore air resistance so that there is no acceleration in the x direction. The vector equations thus obtained yield the following component equations:
x = vx0 t,andvx = vx0,
y = h0 + vy0 t - g t 2 / 2,
vy = vy0 - g t.Because the vectors live on a plane, they have direction as well as magnitude. The direction of a position vector is the direction from the origin to the position of the object. The magnitude of a position vector is the distance from the origin to the object. Likewise, the direction of a velocity vector is the direction of its motion, and the direction of an acceleration vector is the direction of its acceleration. Note that the direction of the acceleration vector is independent of the direction of the velocity vector. When the acceleration vector points in a different direction from the velocity vector, it means that the object is changing direction (ie., from V1 to V2):

If we measure a vector, we can use right triangle trigonometry to find its components. For a triangle with acute angle "θ", hypotenuse of length "h", and sides of length "a" and "o" adjacent and opposite to the angle θ, respectively,
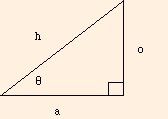
the sine and cosine of the angle are given by
sin θ = o / hand
cos θ = a / h.Similarly, given the vector with length V and direction θ from the horizontal:
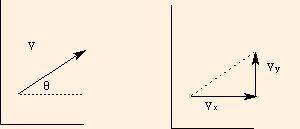
We find its x component as
Vx = V cos θand its y component as
Vy = V sin θ.Implicit in these equations is the fact that the original vector V is drawn along the hypotenuse of a right triangle. The right triangle was constructed by drawing a horizontal line from the origin of the vector and dropping a perpendicular from its other end to the horizontal line. The components of the vector (relative to the angle θ) always correspond to the adjacent and opposite sides.
It is important to note that the connection of cosine to x component and sine to y component is not invariant. In the following drawing,
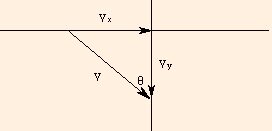
we have
Vx = V sin θand
Vy = V cos θ,because of the way the angle was labeled. Similarly, we can find the components of a vector V which are parallel and normal (perpendicular) to a given direction W:
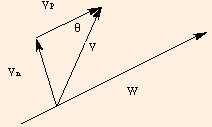
by
Vp = V cos θand
Vn = V sin θ.That is, we are not tied to the x and y axes when using vectors. Here we drew the triangle by raising a perpendicular (to W) from the origin of the vector, and then drawing a line (which is parallel to W) to the other end of the vector. It is also useful to be able to find the angle of a vector from the horizontal (or some other reference direction), given its components:
θ = tan-1 (Vy / Vx),since
Vy / Vx = sin θ / cos θThere are several operations on vectors which we will have need to perform:= tan θ.
Addition:We will also define a "unit vector" for a vector V:V1 + V2 = (V1x + V2x, V1y + V2y)Subtraction:V1- V2 = (V1x - V2x, V1y - V2y)Length:Length (V) = Sqrt (Vx2 + Vy2).
v = V / Length (V),which is a vector of length one pointing in the same direction as V. Note that the equation for the length of a vector is simply Pythagoras' celebrated theorem.
The abstraction of vectors to three dimensions is straight forward, but we will have little occasion to need them in this course.
This applet will give you some practice in converting between vector representations; when you have answered all of the questions correctly,
it will show you the sum vector in green. Hints: 1) since vectors can be used to describe any quantity which has length and direction,
this program does not check units; and, 2) the angle between the sum vector and the x axis is always taken to be positive!
Conservation of momentum, when applied to two objects colliding in two dimensions, can be expressed as
Consider the following collision:
The numbers refer to angles relative to the coordinate axes (remember that we must establish a coordinate system to analyze any vector problem). Assume that the objects are both of mass 1 kg, and the object approaching from the left (#1) is moving at 2 m / s, while the one approaching from the bottom (#2) is moving at 1 m / s. The problem is to find their final speeds.
The momenta are
P 1 y before = 2 sin 30,
P 2 x before = 0,
P 2 y before = 1,
P 1 x after = - P 1 cos 75,
P 1 y after = P 1 sin 75,
P 2 x after = P 2 cos 45
These have the solution
©2006, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
A Physical Example: Conservation of Momentum
P 1 x before + P 2 x before = P 1 x after + P 2 x after
and
P 1 y before + P 2 y before = P 1 y after + P 2 y after.
In these equations, the number refers to the object and the letter refers to the component of the vector.
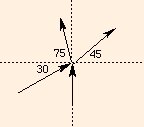
P 1 x before = 2 cos 30,
and
P 2 y after = P 2 sin 45.
The conservation equations are then
2 cos 30 + 0 = - P 1 cos 75 + P 2 cos 45
and
2 sin 30 + 1 = P 1 sin 75 + P 2 sin 45.
P 1 = 0.22 kg m / s
and
P 2 = 2.53 kg m / s.