Isometries
- Every isometry of Rn is a composition of at most n+1 reflections in hyperplanes. (Ratcliffe, Th. 4.1.2)
- O(n) is the isometry group of Sn-1.
SO(4) is isomorphic to (S3 ⊗ S3) / C2
(Thurston, pp. 64,107) - Let En be the one-point compactification of Rn with the point at ∞ (homeomorphic to Sn).
A Moebius transformation of En is a finite composition of inversions in spheres.
An inversion smoothly exchanges the interior with the exterior, keeping the sphere fixed. Inversions are conformal: they preserve angles. They also preserve orientation.
These transformations form the Moebius group. The group of Euclidean isometries is a sub-group of the Moebius group. (Ratcliffe, p. 111) - The Moebius group Moeb(En-1) is the isometry group of Hn. (Ratcliffe, p. 132)
- Euclidean similarities are generated by O(n), scalar dilations and translations. There are no hyperbolic or spherical similarities.
The subgroup of Moebn-1 which takes an Sk to itself is isomorphic to Moebk ⊗ O(n-k).
Moebn is equivalent to the homeomorphisms of Sn which map Sn-1s to each other.
(Thurston, pp. 61, 62, 83)
On Surfaces
- The sum of the interior angles of a flat n-gon is (n-2) π radians.
If the n-gon is embedded in a surface of positive curvature, the sum is greater; if it is embedded in a surface of negative curvature, the sum is less.
- A compact oriented surface S embedded in a manifold M is
incompressible if it is not a topological disc
and for every element in π1(S) there
is a unique matching element in π1(M) (the
inclusion π1(S) → π1(M) is
injective; π1(M) may have more
elements than π1(S)). (Marden, section 3.7)
Alternatively, a disc D embedded in M whose boundary is embedded in S is a compression disc for S if the boundary of D does not bound a disc in S. If such a disc exists, S is compressible. (Purcell, p. 150)
For example, let S be a genus 2 torus and D be a disc whose boundary intersects S between the holes. D is a compression disc. D divides the genus 2 torus into two genus 1 tori (with appropriate surgery).
-
An essential surface S is embedded in a manifold M such that
the intersection of S and ∂M is ∂S, where the components of ∂S
are not homotopic to a point in ∂M.
The latter rules out a disc which "slices" a piece off the "end" of a solid torus.
A compression disc is essential. (Marden, section 3.7) -
Every orientable surface bounds a compact 3-manifold.
Every non-orientable surface of even genus bounds a compact 3-manifold. (Hirsch, p. 193, 194) - No complete C2 surface of constant negative curvature can be embedded in R3. (Ratcliffe, p. 12)
A closed hyperbolic surface can be smoothly (C∞) and isometrically embedded in R17. A noncompact hyperbolic surface can be smoothly and isometrically embedded in R51. (Marden, section 2.7)
-
The area of a closed surface of genus g, with n punctures and m cone points (orders ri) is
2π/k (2 - 2g - n - Σ (1 - 1/ri))
(k = 1 for S2 / G, -1 for H2 / G) (Marden, section 3.14)
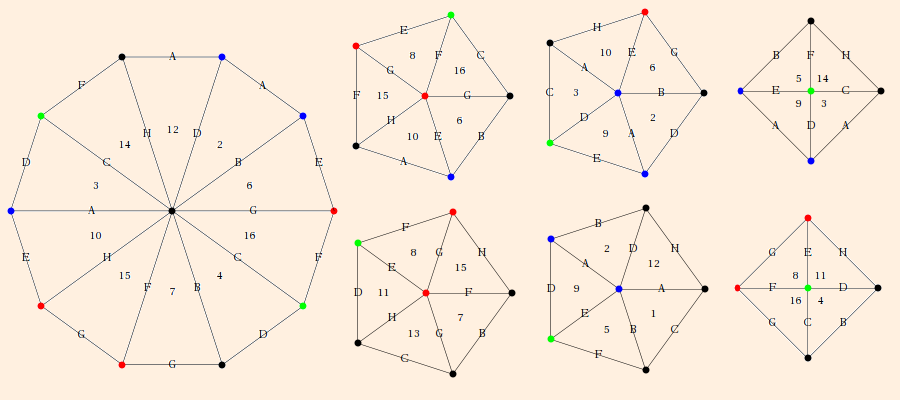
Examples
- Some planar constructions:
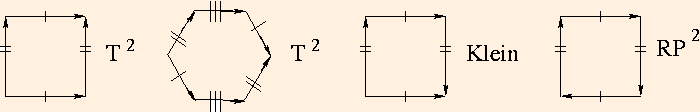
The two tori represent rectangular and hexagonal tilings of the Euclidean plane, respectively.
After identifying the single-hashed sides of the hexgonal torus, the resultant "penne" must be twisted 180 degrees before the other sides will match up. (Thurston, p. 5)
Omit the singly-hashed identification on the Klein bottle to make a Moebius strip. (Henle, p. 106, 111, 112)If you want to construct these, use a large piece of cloth and safety pins. Make each identified edge pair a noticeably different length, and pin them in the order of longest to shortest. It helps to use an additional set of pins for the identified vertices to keep them organized as you pin.
Since the boundary of a Moebius strip is S1, we can remove a B2 from an S2 and glue in a Moebius strip to obtain RP2. Do it twice to obtain a Klein bottle. This operation is termed adding a cross-cap.A simple notation is often used in such constructions. Label each singly-hatched side "a", each doubly-hatched side "b" and each triply-hatched side "c" (etc.). Then, typically starting with an "a" side whose direction is clockwise, proceed clockwise; whenever the side's arrow is parallel to your clockwise direction, write the letter; when the side has an arrow which is in the opposite direction, write the letter as an inverse. Hence we have:
- rectangular torus: a b-1 a-1 b
- hexagonal torus: a b-1 c-1 a-1 b c
- Klein bottle: a b a-1 b
- RP2: a b a b
A sphere with g cross-caps has χ = 2 - g. (Edelbrunner and Harer, p. 34, 36)
-
The torus can tile the Euclidean plane because at each vertex, four tori meet, and the interior angles add
up to 2π. Similarly with the hexagonal torus: at each vertex, three tori meet, and again, the sum of
the interior angles is 2π. For surfaces of higher genus (often called handlebodies), a
Euclidean tiling is not possible. But a tiling of H2 is.
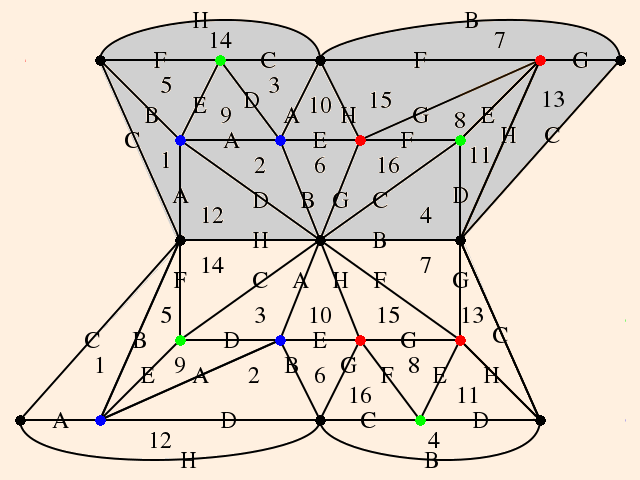
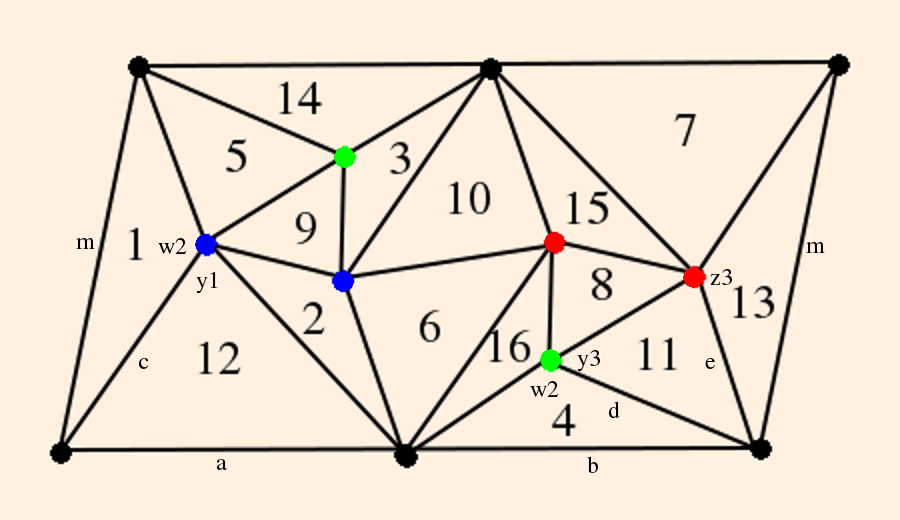
Consider a surface of genus 2. A two-holed torus can be constructed using identifications on an octagon:
a b a-1 b-1 c d c-1 d-1
(Another construction identifies parallel sides; this can also be done with a decagon to produce a genus-2 torus.)An interior angle of a regular octagon is 3π/4. At each vertex, two octagons is not enough and three is too many. But as we see below, χ for the genus-2 torus is -2, which means that it can only be given a hyperbolic structure. When the octagon is embedded in H2, the sides become curved; by an appropriate choice of size for the octagon, the interior angles will be π/4, and the octagon can then be used to tile H2.
(Thurston, section 1.2)
-
An identification of the sides of a 4g-gon of the form
a1 b1 a1-1 b1-1 ... ag bg ag-1 bg-1
will produce a genus-g torus. There are many identifications which will produce the same handlebody. In most cases twists (as in the hexagonal torus) will be requiredAn identification of the sides of a 2g-gon of the form
a1 a1 ... ag ag
will produce a non-orientable genus-g surface. All non-orientable surfaces can be obtained this way. Any two non-orientable closed surfaces with the same χ are homeomorphic.(Thurston, p. 26)
-
(Gray, p. 46 (1)) (Henle, p. 167 (2), 193 (3), 295 (4)) (Hu, p. 28 (5))surface b1 b2 χ π1 E2 0 1 2 0 H2 0 1 2 0 annulus 1 1 0 Z cylinder 1 1 0 Z disc 0 1 1 0 S2 0 1 2 (4) 0 T2 2 1 0 (2) Z ⊗ Z Riemann surface genus g 2 g 1 2 - 2 g (4) Z 2g | aba-1b-1cdc-1d-1... = 1 (Bott and Tu, p. 240) Moebius strip 1 0 0 Z Klein bottle 2 (3) 1 (3) 0 (2) Z ⊗ Z | abab-1 = 1 RP2 0 0 1 (2) Z2 connected sum of n RP2 n - 1 0 2 - n (4) Zn | aabbcc... = 1 (1) non-orientable surface genus g g - 1 (5) 0 (5) 2 - g - If P is an irreducible (unfactorable) polynomial of two complex variables, P=0 describes a Riemann surface.
xn + yn = 1 for n>1 describes a Riemann surface of genus ½(n-1)(n-2).
The Uniformization Theorem states that a simply connected Riemann surface can be conformally mapped into exactly one of S2 (if χ > 0), C (if χ = 0) or B2 (if χ < 0).
The group of conformal automorphisms of a Riemann surface is discrete IFF π1 is nonabelian. For g ≥ 2, it has at most 84(g-1) elements.
A Riemann surface admits a positive-definite metric of the form ds2 = E du2 + 2 F du dv + G dv2. Such a metric has area element √ (E G - F2) du ∧ dv.Every Riemann surface whose π1 is nonabelian admits a hyperbolic metric compatible with its complex structure. It has finite hyperbolic area IFF it is a closed surface with n punctures (open discs removed) and 2g+n≥3.
(Marden, sections 2.7, 2.9)
Classification
- Every oriented, closed 2-manifold is the quotient of either S2, E2 or H2, by
a discrete subgroup of isometries acting freely on it.
(Borisenko, p. 2)
Every closed 2-manifold is homeomorphic to S2, a connected sum of tori, a connected sum of tori and one projective plane, or a connected sum of tori and one Klein bottle. (Averett, p. 4)
Every compact, connected 2-manifold is topologically equivalent to a sphere (2-cell notation aa-1), a connected sum of tori (aba-1b-1cdc-1d-1...), or a connected sum of projective planes (aabbccdd...). Every compact, connected 2-manifold with boundary is equivalent as just stated, with some finite number of discs removed. (Henle, p. 122, 129) (Christenson, p. 439)
Every compact connected surface is diffeomorphic to S2 - some number of B2, with either I2 or Moebius bands connecting the holes.
Two surfaces are diffeomorphic iff they have the same genus, Euler characteristic and number of boundary components.
Two surfaces are diffeomorphic iff they have the same Euler characteristic and number of boundary components, and are both either orientable or non-orientable.
Every connected compact orientable 2-manifold is diffeomorphic to the surface obtained from an orientable surface of genus 1 - (χ + δ) / 2 by the removal of δ disjoint B2. (Hirsch, p. 189, 205, 207)
Every open surface admits a hyperbolic structure. (Scott, p. 421)
- The Euler characteristic of a surface can be computed from its triangulation as
χ = #vertices - #edges + #faces
A closed surface has hyperbolic, Euclidean or spherical (elliptical) structure iff its Euler characteristic is negative, zero or positive, respectively.
This holds for surfaces in general, except that surfaces homeomorphic to R2, S1 ⊗ R or the Moebius strip can be given both Euclidean and hyperbolic structures. (Thurston, p. 28, 118) - Removal of an open disc reduces the Euler characteristic by 1.
The Euler characteristic of a surface formed by gluing two surfaces with boundary along a boundary component is the sum of the original Euler characteristics.
Note that RP2 is equal to a Moebius strip glued to a disc.
The Euler characteristic of the union of two surfaces is equal to the sum of their Euler characteristics minus the Euler characteristic of their intersection.A sphere with g handles, c cross-caps and d open discs removed has Euler characteristic
χ = 2 - 2g - c - d
Isometries
-
Moebius transformations on E2 can be written as
f(z) = (a z +b) / (c z + d),
where a, b, c and d are complex numbers subject to a d ≠ b c (the usual normalization is a d - b c = 1, which makes the group isomorphic to PSL(2,C)). These are the most general functions on E2 which map circles to circles.f(z) is often represented as a matrix:
Conjugation can be used to effect a coordinate transformation on an iterated Moebius map {z, f(z), f2(z),...}.
(also denoted ((a,b),(c,d))). If the trace of f(z) (Tr(f) = a+d) isa b c d - <-2 or >2, f is loxodromic: a screw motion (conjugate to z → λ2z, |λ|>1);
- <-2 or >2 and real, f is hyperbolic: a loxodromic transformation with λ>1 (this term sometimes is used to include loxodromic);
- >-2 and <2 and real, f is elliptic: a rotation (conjugate to z → e2iθz, θ ≠ π; NB: z → -z is conjugate to z → 1/z);
- equal to ±2, f is parabolic: a Euclidean translation on the sphere at ∞ (conjugate to z → z+1).
A parabolic map has a single fixed point; a loxodromic, hyperbolic or elliptic map has two fixed points.
Some convenient trace identities are:- Tr(f) = Tr(f-1)
- Tr(gfg-1) = Tr(f) (Tr is unchanged by conjugation)
- Tr(product) is unchanged under cyclic permutation of the product
- Tr(fg) = Tr(f-1g-1)
- Tr(fg) + Tr(f-1g) = Tr(f) Tr(g)
If Tr(f) = 0, f2 = I (so f is elliptic).
Suppose groups G and H of Moebius transformations are each generated by two parabolic elements. G and H are conjugate (therefore isomorphic) if their invariants Tr(ab)-2 are equal up to sign. (Lyndon and Ullman, p. 1388)
The set of all points in E2 that can be reached by iteration of the maps in a Moebius sub-group G is called the regular set (Ω(G)) of the group. It has either one, two, or infinitely many connected components, each of which is either simply connected or contractible (to a point).
Considering the quotient space obtained by Ω(G) / G.Λ(G) ≡ E2 - Ω(G) is called the limit set. These are the fixed points of G. If G has only elliptic elements, it is finite and Λ(G) is empty. If Λ(G) is not empty, it has one, two, or uncountably infinite points.
In the latter case it is a closed set, whose components are either topologically circles, fractal sets, or totally disconnected (every component is a point). (Marden, sections 2.4.1, 2.8)
(Series, p. 8)It turns out that if G has no elliptic elements, the quotient space is the boundary of a hyperbolic 3-manifold M = H3 / G, where π1(M) = G and ∂M ≡ Ω(G) / G. If G contains elliptic elements, M is an orbifold. Unless specified below, we will assume G contains no elliptic elements.
Restricting ourselves to 2-generator groups, generators a and b with inverses A and B, respectively:The fundamental group of ∂M is isomorphic to G, which means the Kleinian groups constitute representations of the fundamental group for a given quotient space topology.
- if G is a translation, ∂M is T2;
- if G is a hyperbolic group of rank n operating on 2n disjoint Jordan
(simple plane closed) curves
(with disjoint interiors) such that each group element maps the inside of one curve
to the outside of a second,
and the inside of the second to the outside of the first (such curves are
paired),
∂M is a surface of genus n (G is a
Schottky group), and Λ(G) is totally disconnected:

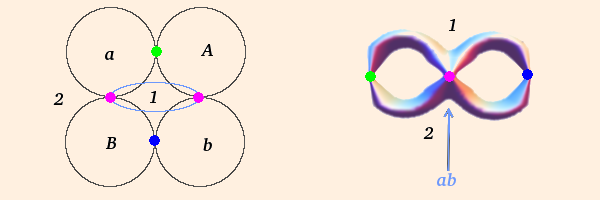
- if G is a hyperbolic group of rank two operating on mutually tangent paired curves
(a paired to A, b paired to B, as below),
whose points of tangency are fixed, and whose commutator
abAB has trace -2, ∂M is
a surface of genus two with a cusp pinch (puncture); a pair
of once-punctured tori:
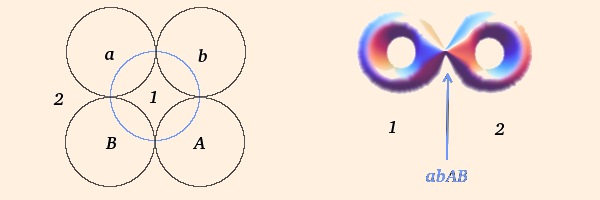
The limit set passes through the points of tangency, which are fixed by cyclic permutations of abAB, and the group is called a quasifuchsian group. If the curve is a circle (as above) the group is Fuchsian and the traces of all the group elements are real.
The region exterior to the paired curves is made up of two disjoint tiles (labeled "1" and "2" above), which become the two sides of the torus separated by the puncture. All quasifuchsian groups yield the same type of quotient surface.
rank 2 with 1 parabolic → genus 2 with 1 element of π1 pinched → 2 once-punctured tori
Λ(G) of such a group (with Tr(abAB) = -2) is a closed curve: a quasicircle, which separates Ω(G) into two disjoint regions; one is tiled by the ideal quadralateral "1", the other is tiled by the ideal quadralateral "2":
In general, if tr(abAB) = 2, a and b share a fixed point; a point fixed by a parabolic operator induces a puncture on ∂M, and each puncture increases the dimension of π1 by 1;
The images here and below are the results of randomly iterating nontrivial products of a, b, A and B, up to 200 factors each, on the fixed points of a, b, A, B, abAB, AbaB, BabA and ABab, for a reasonably large number of iterations on each fixed point.
- if G is a parabolic group of rank two (a and b are both parabolic) operating on two disjoint pairs of tangent circles (one pair for each
generator), ∂M is a surface of genus two with two punctures, equivalent to a sphere with four punctures:
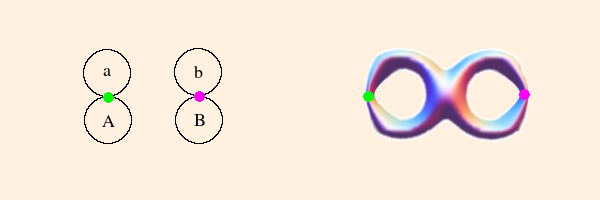
The green point is the fixed point of a, and the magenta point is the fixed point of b. The region external to the circles corresponds to the surface of the 4-punctured sphere.
rank 2 with 2 parabolic → genus 2 with 2 elements of π1 pinched → 4-punctured sphere
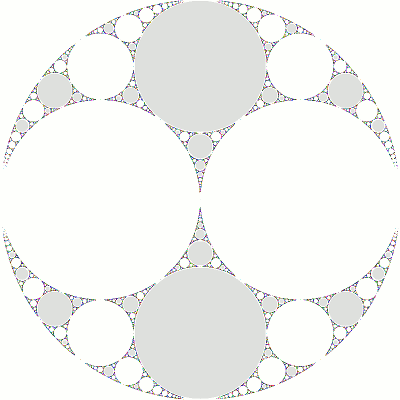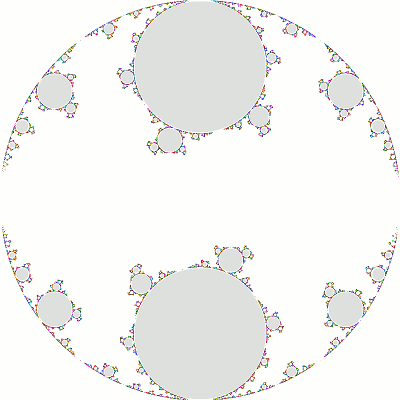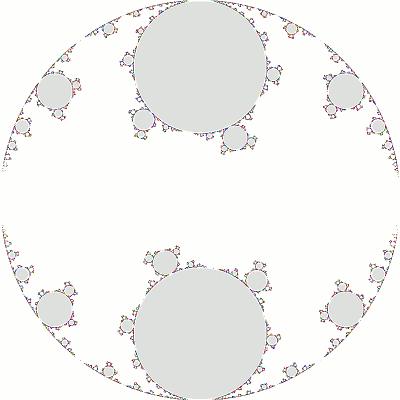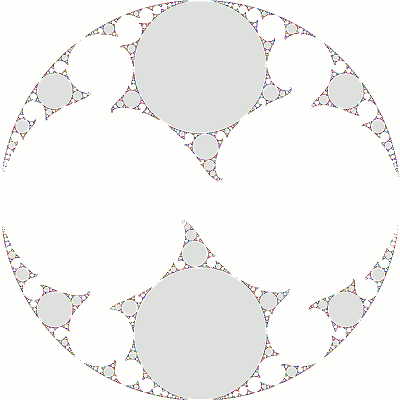
Using the Riley parameter λ, we have a = ((1,2),(0,1)) and b = ((1,0),(λ,1)). Tr(ab) is 2(1+λ) and Tr(abAB) is 2(1+2λ2). The Riley slice is the corresponding 1-complex-dimensional slice of Teichmuller space for groups of two generators. The only point of contact with the Maskit slice (below) is the point λ=i, corresponding to the (0,1) gasket (μ=-2i).
The Riley slice is symmetric about both the real and imaginary axes. Here is a portion of the limit set for λ=0.05+0.93i:

To make this image, a and b were conjugated by ((i,-1),(1,-i))/√2 so that the points at real ∞ have been translated to (0,i) and the origin has been translated to (0,-i).
- if G is a parabolic group of rank two (a and b are both parabolic) operating on mutually tangent paired curves (as below) with Tr(abAB) = -2, ∂M is a surface of genus two with three punctures, equivalent to a pair of triply-punctured spheres:
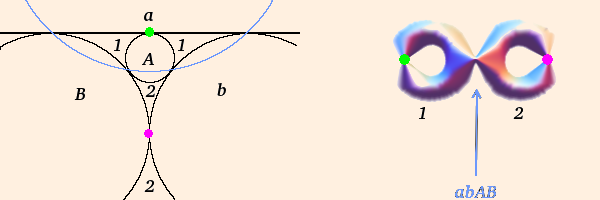
As drawn, the radius of circle "a" is infinite; the green point is the fixed point of a, and the magenta point is the fixed point of b.
rank 2 with 3 parabolic → genus 2 with 3 elements of π1 pinched → 2 thrice-punctured spheres
For each additional independent parabolic element (besides abAB), one half of the regular set closes up into a set of tangent discs:
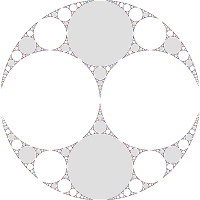
The sets of tiles (on each side) are disjoint from each other.
When constructing the quotient space ∂M, all of the gray discs are identified, and the white discs will similarly be identified
(the gray region outside the limit set is a disc after adding in the point at ∞).
NB: The map maps circles, not discs; here we have colored them in to facilitate identification.
The circles are also iteratively mapped, so not all circles which should be gray are necessarily colored in.We will call such groups gasket groups (also called double-cusp groups).
An acylindrical manifold is boundary incompressible and contains no essential cylinders. Such a manifold M of genus g with n punctures has 3g+n-3 simple loops which divide M into 2g+n-2 "pairs of pants", and whose corresponding group elements can become parabolic in the algebraic limit. Hence each of the loops can be pinched to become a puncture, and each pair of pants becomes a component of ∂M.
(Marden, section 5.3)
- if G is a modular group of rank two (all matrix elements ∈ Z), with both generators and their product parabolic, operating on paired curves (as below), ∂M is a joined pair of triply-punctured spheres:
(Here, the blue circle represents the actions of ab and ba.)
This modular group is unique up to conjugation, and the space is rigid (Marden, section 2.10);
- if G is a group of rank two where there exist group elements which are parabolic permutations of apBq (p and q relatively prime integers), ∂M includes a once-punctured torus component with a (p,q) Dehn twist.
Here, only one side of Ω(G) has closed up into a set of tangent discs; the part of ∂M corresponding to them is a triply-punctured sphere. The other side is simply connected, and its portion of ∂M is the once-punctured torus:
It is instructive to look at the discrete groups associated with the first few values of p and q. There are only 9 independent ones for p or q ≤ 5 because translations of μ by ±2k (k ∈ Z) are equivalent; also, the negative of the complex conjugate of μ yields the same limit set, but reflected in the imaginary axis. For each limit set below, the associated parabolic word is in parentheses: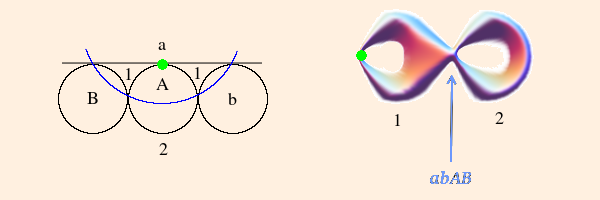

rank 2 with 2 parabolic → genus 2 with 2 elements of π1 pinched → 1 once-punctured torus plus 1 thrice-punctured sphere
G is a single-cusp group.An apBq group element can be found by constructing the set starting with {1}, adding q or subtracting p so that the elements are always positive and never greater than p+q, until you return to 1. The group element is the product of a's and B's created from writing an a for each subtraction and a B for each addition (in reverse order). For instance, the 2,5 set is
{1, 6, 4, 2, 7, 5, 3, 1}
and the corresponding group word is aaaBaaB. This is simply an arithmetic prescription for a consistent winding of q a's and p B's around the torus.If we want G to be a gasket group, we will force Tr(b) to be 2 and look for a p,q element to be the other parabolic element (abAB will be parabolic with our parameterization). ∂M will then be a pair of triply-punctured spheres.
Parameterizing a by the Maskit parameter μ we have a = ((-iμ, -i), (-i, 0)) and b = ((1, 2), (0, 1)). The trace of the 2,5 group element is
-i (μ5 - 4μ4 + 9μ3 - 12μ2 + 9μ - 4),
which must be ±2, from which we can obtain μ.- Since -1 < im(μ) < 1 cannot yield a discrete group,
- and μ and its complex conjugate yield conjugate groups,
- we need only consider μ with im(μ) ≥ 1
- (im(μ) > 2 always yields a discrete group).
We therefore have three possible solutions: 0.375189 + 1.30024i, 1.06548 + 1.2824i and 0.766588 + 1.64214i. When generating Λ(G)s of the first two, one obtains chaotic, overlapping patterns characteristic of non-discrete groups; but the last one yields a discrete group (see below).
For p or q < 0, begin with -p,1, for which the parabolic word is abp, and 0,1 (parabolic word a). For any p,q find relatively prime integers r,s for which ps - rq = ±1. A new parabolic word will be
w(p+q),(r+s) = wp,qwr,s.
So, for example, w-1,2 = w-1,1w0,1 = aba.(This construction works for positive p and q as well.)
p,q and -p,-q will produce the same word.So we can generalize that ±p,q are equivalent under reflection, and that p+kq,q (k ∈ Z) are equivalent under translations.0,1 (a) 
0,3 (aaa) 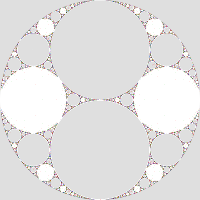
0,4 (aaaa) 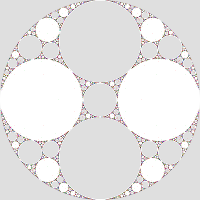
0,5 (aaaaa) 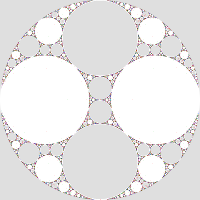
1,2 (aaB) 
1,3 (aaaB) 
1,4 (aaaaB) 
1,5 (aaaaaB) 
2,5 (aaaBaaB) 
±1,1 and ±2,1 and ±3,1 and ±4,1 and ±5,1 are translations of 0,1 (0,2 is the same as 0,1);
-5,2 and -3,2 and -1,2 and 1,2 and 3,2 and 5,2 are equivalent under translation;
-5,3 and -2,3 and 1,3 and 4,3 are equivalent under translation;
-4,3 and -1,3 and 2,3 and 5,3 are equivalent to 1,3 under reflection (and translation);
-3,4 and 1,4 and 5,4 are equivalent under translation;
-5,4 and -1,4 and 3,4 are equivalent to 1,4 under reflection (and translation);
-4,5 and 1,5 are equivalent under translation;
-1,5 and 4,5 are equivalent to 1,5 under reflection (and translation);
-3,5 and 2,5 are equivalent under translation; and
-2,5 and 3,5 are equivalent to 2,5 under reflection (and translation).Note that 0,3 and 0,4 and 0,5 are non-free; in each case the associated parabolic word is -I (where I is the identity matrix). The limit sets do not bound discs; they are fractal dust. The same holds true (up to sign) for all 0,q for q > 2.
- Limit sets for groups which are not discrete are essentially random; given an infinite amount of time, the program will eventually fill the complex plane:

G is discrete iff Λ(G) has no points in the interior of H3. (Purcell, p. 102)
- There are relatively prime integers r and s such that ps - qr = ±1. If α is a simple geodesic loop with slope p/q and β is a simple loop with slope r/s, the geometric intersection number
ι = | ps = qr |
is the number of times α crosses β on the quotient surface. (Marden, problem 2.6)- Values of μ associated with irrational windings produce singly (below left) or doubly (below right) degenerate groups: one or both sides of Ω(G) has zero area, and Λ(G) (of dimension 2) completely fills the region(s):


On the left, μ = 0.7056734968-1.6168866453i; on the right, a = ((1,0),(1,1)) and b = ((1,ei π/3),(0,1)) , corresponding to the figure 8 knot complement (below).
In both cases, Λ(G) is incomplete; on the left, given infinite time the program would completely fill in the white region outside the gray circles (which constitute, with the exterior region, the non-degenerate part of Ω(G)); on the right, given infinite time the program would fill the entire complex plane (the voids are near parabolic fixed points which correspond to infinite word lengths).Degenerate groups are discrete and geometrically infinite (but M(G) may have finite volume).
The limit set of a doubly degenerate discrete group is the entire sphere at ∞. This is also true for closed hyperbolic manifolds. (Thurston, p. 172)
The irrational slope of the winding is the ending lamination for the associated cusp. (Marden, problem 2.6)- Groups for which some product of generators is equal to the identity are not free; they are not quasifuchsian (their limit sets are fractal dust).
- Groups with three or more generators and tangent paired curves yield more complex quotient spaces (tori with multiple punctures, spheres with more punctures, etc.)
For example, let
a = ((1 + 2i, 4), (1, 1 - 2i)),
a and b have trace 2, and c, aB and cbCB have trace -2. This group corresponds to Mumford et. al., figure 11.6; the limit set is conjugate to their figure 11.7:
b = ((1 + 1.5i, 1), (2.25, 1 - 1.5i)) and
c = ((-13 - 4i, 8i), (-12 + 16i, 11 + 4i)).Groups exist for which any of the disjoint sets of circular components can become degenerate (these are called partially degenerate groups).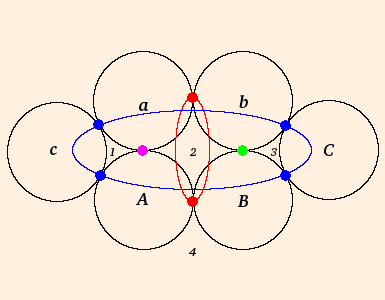
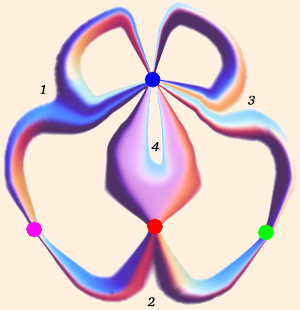

The magenta and green points correspond to the fixed points of a and b, respectively; the red circle corresponds to the action of aB, and the blue circle corresponds to the action of acBC. The quotient surface is four triply-punctured spheres. The limit set has four mutually disjoint sets of components, corresponding to the four numbered tiles.
rank 3 with 6 parabolic → genus 3 with 6 elements of π1 pinched → 4 thrice-punctured spheres
(Mumford et. al., chs. 3, 4, 6, 7, 9, 10)
For any two sets of three points, there is exactly one element of PSL(2,C) which maps the first set to the second. (Thurston, p. 87)
- The moduli space of a surface is the quotient of the space of metrics admissible to the surface, by the action of the diffeomorphisms of the surface (Diff).
The Teichmuller space restricts the diffeomorphisms to those homotopic to the identity by a homotopy which takes the boundary into itself at all times (Diff0).
The mapping class group is Diff S / Diff0 S. Therefore the moduli space is the quotient of the Teichmuller space by the mapping class group.If a surface has empty boundary, two structures of S are equivalent in moduli space iff they have the same holonomy group (up to conjugacy). They are equivalent in Teichmuller space iff they have the same holonomy map.
The mapping class group of T2 is PSL(2,Z) (the projective special linear group acting on pairs of integers).
The Teichmuller space of a compact surface that admits a hyperbolic structure is homeomorphic to R 3 |χ|.
The maximum number of disjoint, non-parallel simple closed curves on a hyperbolic surface is 3g - 3. Cutting the surface along the corresponding geodesics divides the surface into 2g - 2 surfaces homeomorphic to S2 - 3 B2 (pairs of pants). The Teichmuller space of the original surface corresponds to the degrees of freedom defining the lengths of the boundary components of the pants, along with the number of twists with which the pants are glued back together.
The mapping class group of a closed surface is isomorphic to the outer automorphism group of its fundamental group.If there are n punctures, the dimension is 3 |χ| - n (or 6g + 2n - 6). (Marden, sect. 2.10)
For groups of two generators, the quotient space has χ = -2, so the Teichmuller space is 6-dimensional. We can parameterize it by the complex traces Tr(a), Tr(b) and Tr(ab).
The Maskit slice is a 1-complex-dimensional slice of Teichmuller space corresponding to Tr(b) = 2 and Tr(abAB) = -2. The slice has translational symmetry because Tr(ab) = Tr(a) ± 2k, k ∈ Z. From our considerations above, we need only examine the region 0 ≤ Re(μ) < 2, 1 ≤ Im(μ).
On the left, Im(μ) = 2 and Re(μ) varies from 0 to 1.9; on the right, Re(μ) = 1 and Im(μ) varies from 4 to 1.5:

The region outside the unit circle in these plots should be gray, but we have left it white to better show how the limit set "bleeds" out of the unit circle.
As Im(μ) decreases (right), the first seven frames correspond to single-cusp groups: their topology is a triply-punctured sphere (gray discs) plus a (simply-connected) once-punctured torus (white region). As the torus "closes up" (the last remaining loop of π1 becomes "tighter"), the group approaches a double-cusp group. The eighth frame is the (1,2) gasket, and the last three frames are non-discrete. The latter show an increasing "overlap" in the limit sets, but with sufficient time, the limit set will fill all three frames.The "essential" portion of the slice is shown here (with some groups identified by (p,q):
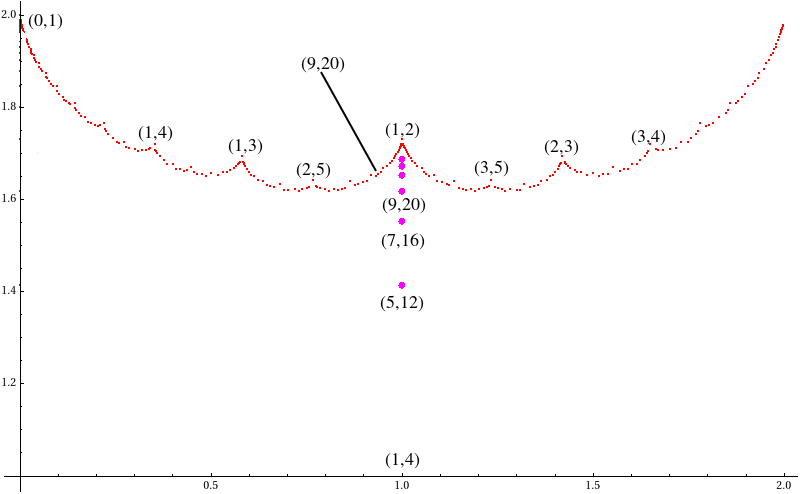
The red points indicate the gasket groups on the Maskit boundary. Groups with values of μ above the boundary are single-cusp groups. Groups below the boundary are almost all non-discrete, with one class of exceptions: the magenta points are non-free groups. Note that a single value of (p,q) (i.e., 9,20) can have solutions to its trace equation which are a gasket and a non-free group (9,20 also has eight non-discrete groups). The non-free groups plotted above are (5,12), (7,16), (9,20), (11,24), (13,28) and (15,32).
Note that the region 0 ≤ Re(μ) < 2 appears to be symmetric about the line Re(μ) = 1. This is due to a combination of symmetries g(μ) ≈ g(μ*) ≈ g(-μ*) ≈ g(μ + 2), or equivalently, g(μ) ≈ g(2 - μ), where here "≈" denotes equivalence up to conjugacy (the "mirror image" groups labeled above are all conjugate).
The slice also shows a pattern in the ratio p/q:
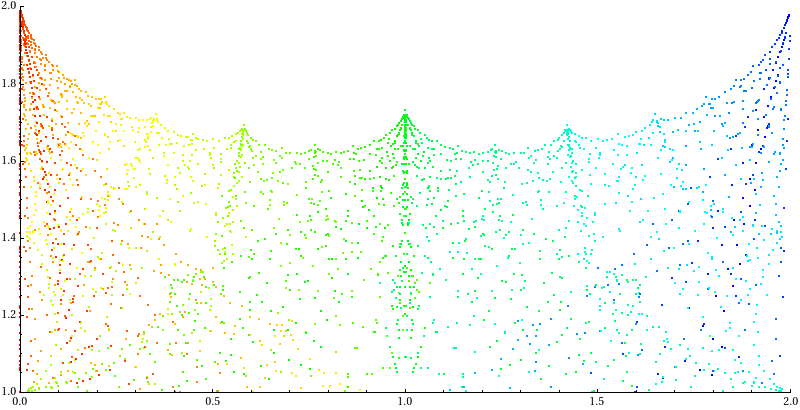
Here red corresponds to p/q = 0 and blue corresponds to p/q = 21/22 (the highest ratio computed for this data set).
(Mumford et. al., ch. 10)
The outer automorphism group is the conjugacy class under diffeomorphisms of maps of π1 into itself.
(Thurston, p. 260, 262, 264, 266, 271, 276, Thurston Notes, pp. 89-91)
On 3-manifolds
- All compact orientable 3-manifolds are boundaries. (Greenberg, p. 240)
- Every 3-manifold can be obtained by gluing together the boundaries of two solid tori of some genus.
This is called a Heegaard splitting.
(Thurston Notes, pp. 1-3)
For a given 3-manifold M, the minimum genus for all possible splittings is the Heegaard genus. The rank of π1(M) cannot be larger than the Heegaard genus. (Marden, section 2.8.1)
- A 3-dimensional gluing of tetrahedra is a manifold iff
χ = #vertices - (2 #edges - 3 #faces + 4 #tetrahedra) / 2
is zero. So χ = 0 for any closed 3-manifold.If X is a 3-space and it has k vertices vk,
When identifying faces of polyhedra, the total number of faces must be even, and every identification must be orientation-reversing between pairs of faces. This produces an oriented manifold except near the vertices, which must be removed in order for the identification to produce a manifold. (Thurston Notes, p. 3)χ(X) = k - ½ Σ χ(link(vk))
(Thurston, p. 122) - A closed 3-manifold is irreducible if every embedded S2 is the boundary of a B3
(there are no essential S2).
If M is orientable and irreducible, then π2(M) = 0. (Scott, p. 483)
- A closed 3-manifold is prime if every separating embedded S2 is the boundary of a B3. The three main classes are
Sphere / Prime Decomposition - every orientable closed 3-manifold has a finite connected sum decomposition into prime manifolds. (Borisenko, p. 8)- S3 / Γ, where Γ is a finite subgroup of SO(4)
acting freely by rotations; Γ = π1(M).
If Γ is cyclic, M is a lens space.
A (p,q)-lens space is generated by Γ = ((e2πi/p,0),(0,e2πiq/p)). Two lens spaces with indices (p,q) and (p',q') are homeomorphic iff p=p' and either q=±q'(mod p) or qq' = ±1(mod p). (Ratcliffe, p. 342)
- S1 ⊗ S2, with infinite cyclic fundamental group. It is the only orientable 3-manifold that is prime but not irreducible, and the only prime orientable 3-manifold with nontrivial π2.
- aspherical manifolds, irreducible with infinite noncyclic π1.
- S3 / Γ, where Γ is a finite subgroup of SO(4)
acting freely by rotations; Γ = π1(M).
If Γ is cyclic, M is a lens space.
- Torus Decomposition - every closed orientable irreducible 3-manifold has a finite collection of disjoint incompressible tori (i.e., cusp tori)
which decompose it into a finite collection of compact 3-manifolds with toral boundary, each of which is either torus-irreducible or Seifert fibered.
A Seifert fibration is a 3-manifold fibered by circles which are the orbits of a circle action which is free except on at most finitely many fibers.
(Borisenko, p. 6, 10)
Examples
- S2 ⊗ S1 is obtained by identifying corresponding points on a pair of S2, one inside the other; it can also be obtained by identifying corresponding points on two congruent solid tori. (Alexandroff, p. 11)
- S3 can be obtained by identifying the surfaces of two solid tori.
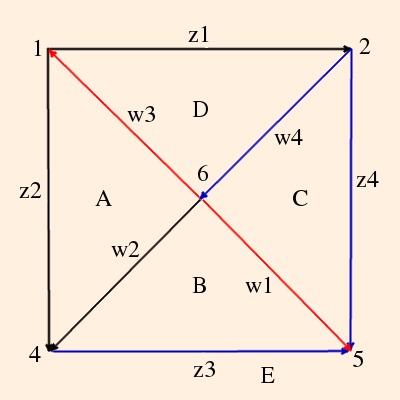
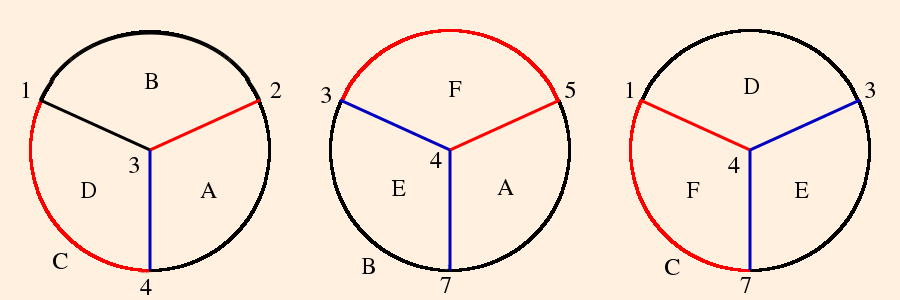
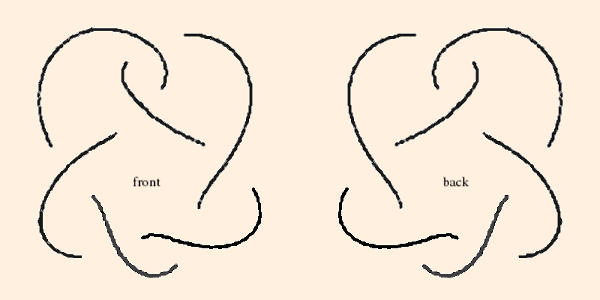
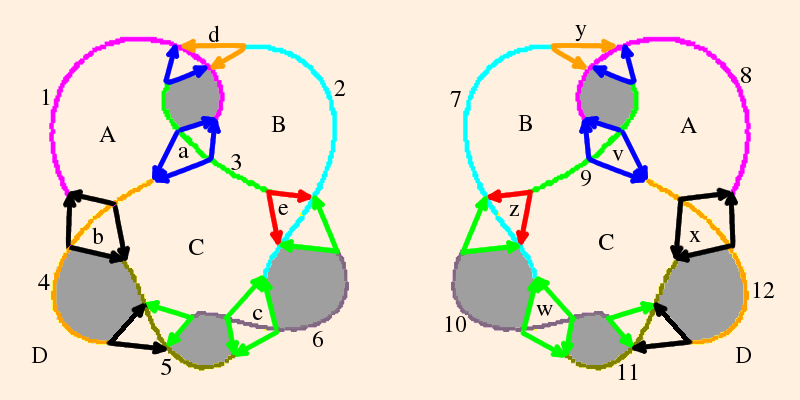
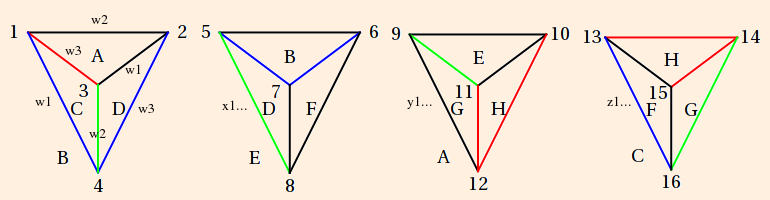
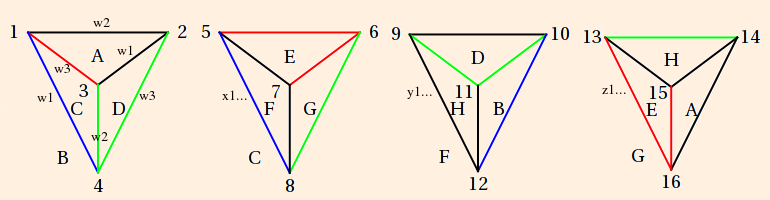
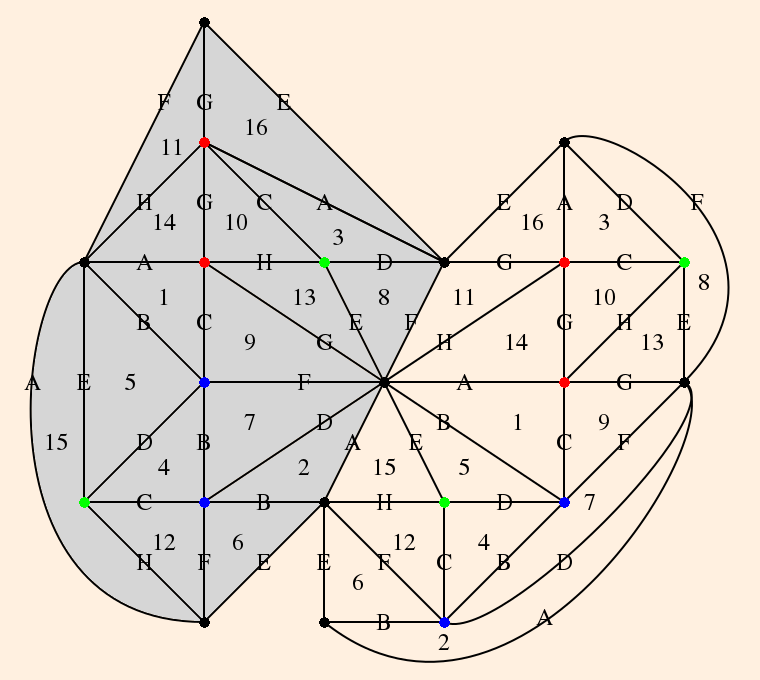
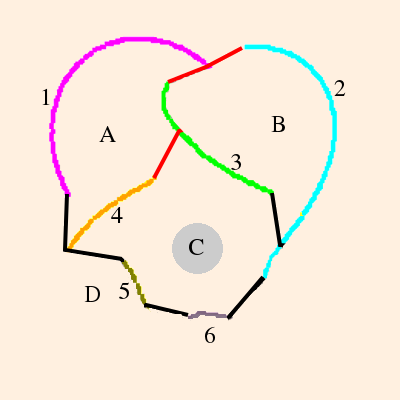
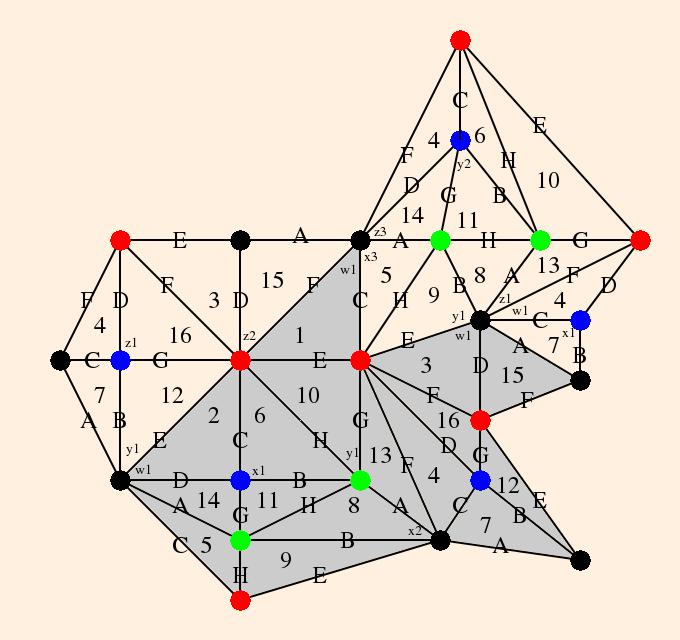
- The figure 8 knot complement is formed as follows. Beginning with the knot itself (notated "4_1"; also "m004"):
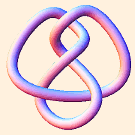
we first draw its (somewhat stylized) skeleton:
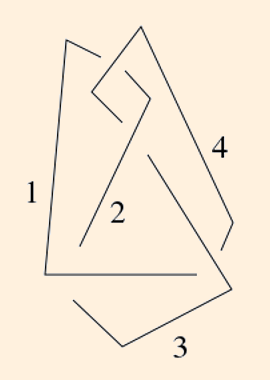
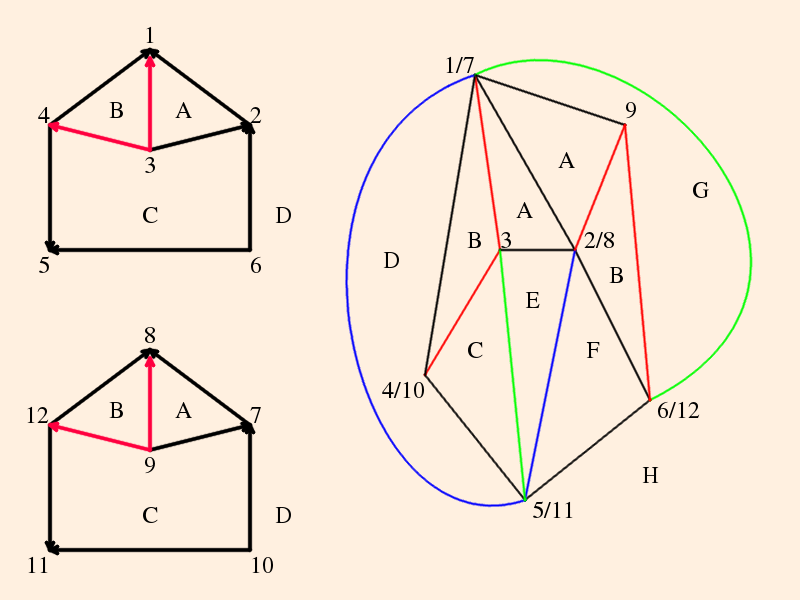
The topology of the knot complement is defined by the under/over-crossings. Since the knot itself is not in the complement, the numbered segments will each become an ideal vertex (located on the sphere at ∞). The crossings will become edges, and the regions in the plane of the knot projects will become triangles:
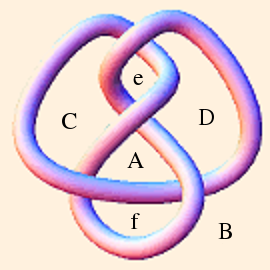
There will be one tetrahedron on this side of the plane, and one on the other (which we will attend to shortly). Triangles A, B, C and D will form the sides of the tetrahedron; regions e and f are bigons (a region bounded by exactly 2 edges and 2 vertices (Purcell, p. 9). These will be collapsed because their edges will be isotopic, by construction.
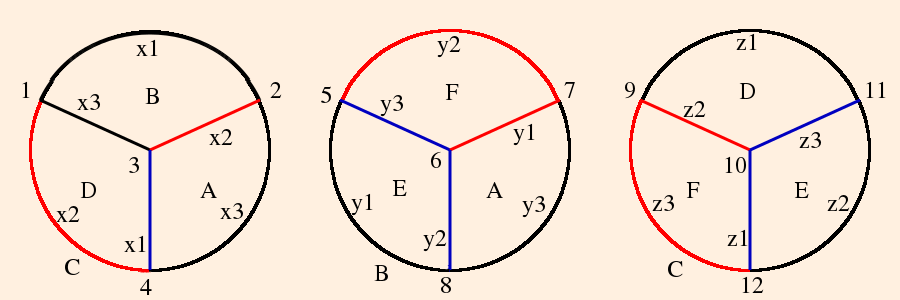
Following (Purcell, section 1.1), we draw in 4 copies of the edge at each crossing:
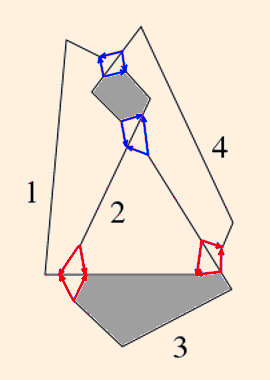
Edges can either be drawn from over-crossongs to under-crossings, or vise versa, but for any given crossing, they must all be one way or the other.
The shaded areas are the bigons, which we now consider collapsed.We see that
- vertex 1 has two red edges leading to it, from vertices 2 and 3, and one blue edge leading to it, from vertex 4;
- vertex 2 has two blue edges leading to it, from vertices 3 and 4, and one red edge leading away from it to vertex 1;
- vertex 3 has two red edges leading away from it, to vertices 1 and 4, and one blue edge leading away from it to vertex 2; and
- vertex 4 has two blue edges leading away from it, to vertices 1 and 2, and one red edge leading to it from vertex 3;
- thus vertices 1, 2 and 3 and their corresponding edges enclose triangle A;
- vertices 1, 3 and 4 and their corresponding edges enclose triangle B;
- vertices 1, 2 and 4 and their corresponding edges enclose triangle C; and
- vertices 2, 3 and 4 and their corresponding edges enclose triangle D.
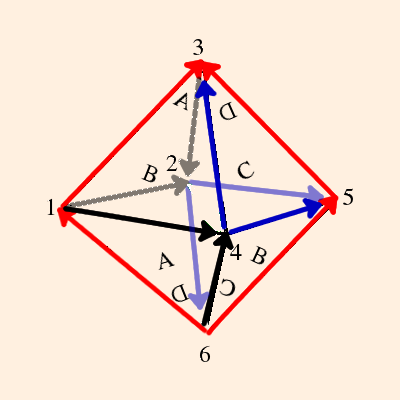
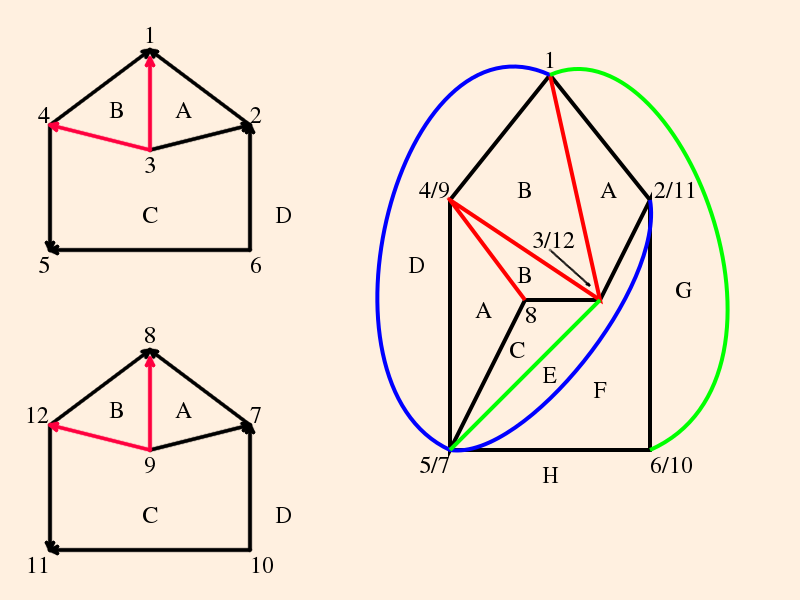
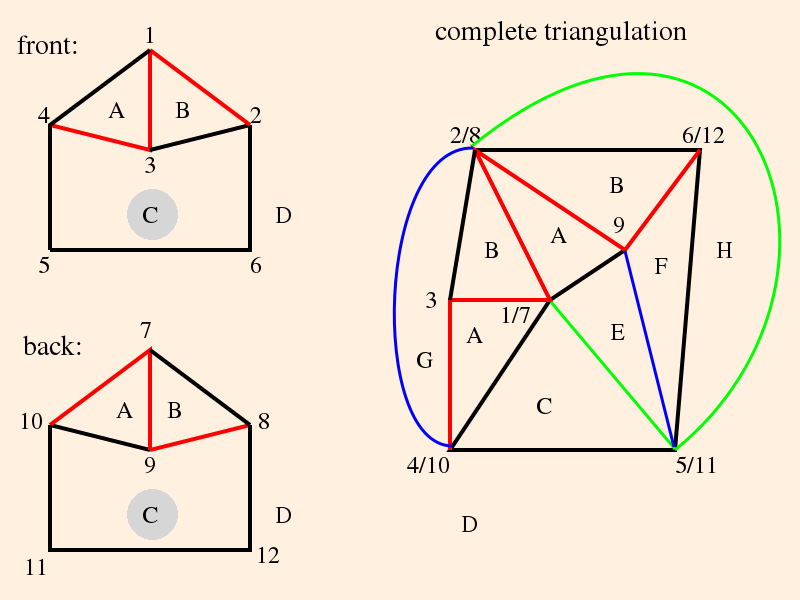
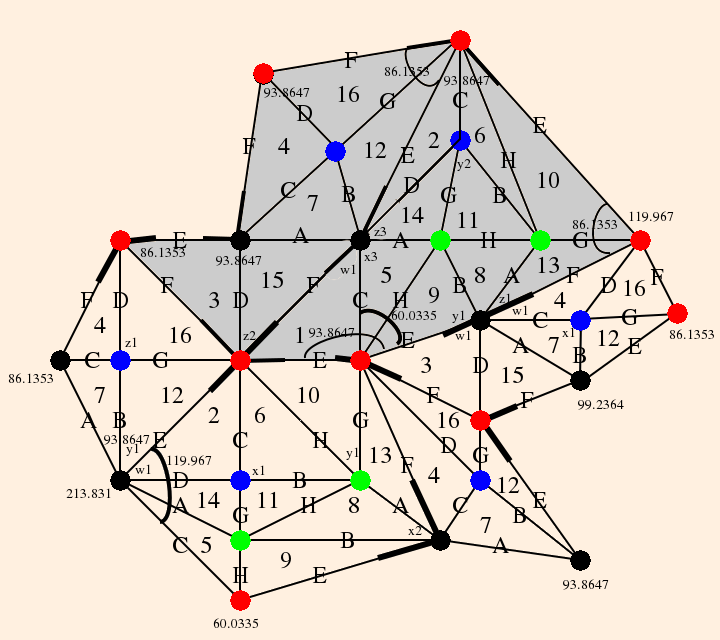
Thus the graph of the tetrahedron on this side of the plane is
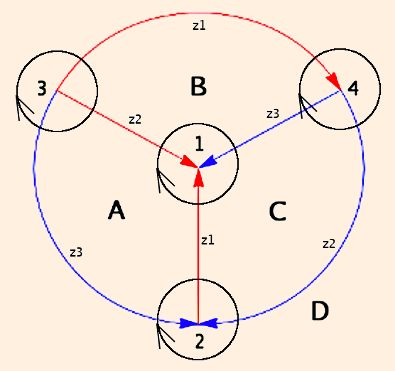
The zi are vertex invariants (defined below); after labeling the vertex angles, each edge opposite a given angle is labeled with that vertex invariant; opposite edges have the same vertex invariants.
The link of each vertex is denoted by the directed circles; since the tetrahedra are ideal, the links are Euclidean triangles.
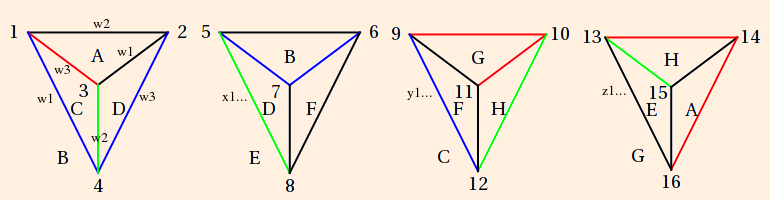
To construct the tetrahedron on the bottom side of the knot plane, we first must turn the knot over:
Notice that what were under-crossings are now over-crossings, and vise versa. Its skeleton is labeled with new vertex numbers to avoid confusion (they will all be identified at the end):
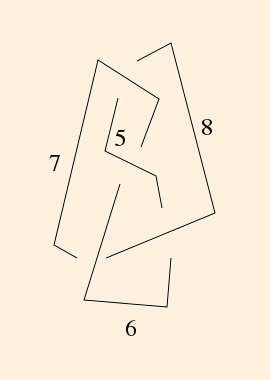

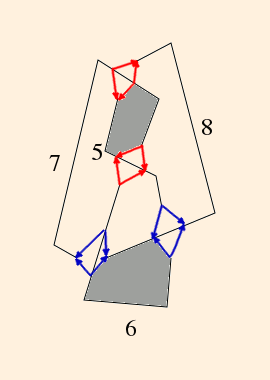
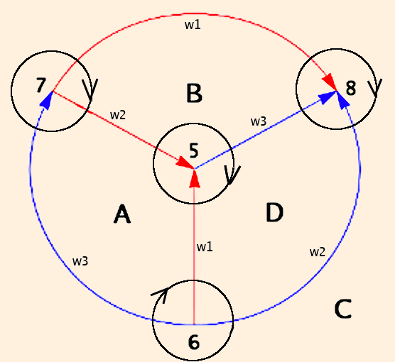
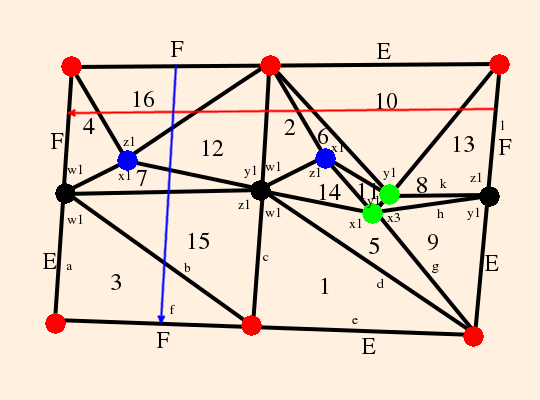
The graph of the tetrahedron on the underside of the knot plane is then
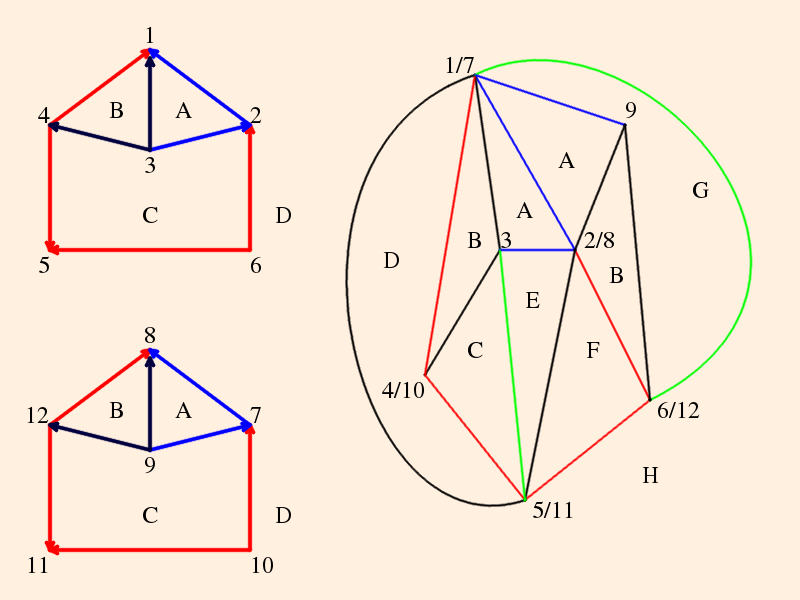
The figure 8 knot complement is composed from the identifications on this pair of ideal equilateral tetrahedra, and removal of the vertex:
- The vertices of the tetrahedra, numbered 1 through 4 and 5 through 8, are all identified,
- the faces of each tetrahedron are identified by letter, and
- all of the red edges are identified, as are all of the blue edges.
The identifications produce an object with 1 vertex, 2 edges, 4 sides and 2 tetrahedra; removal of the vertex (so that χ = 0) makes the object a 3-manifold.
(Any 3-manifold with toroidal boundary will have an equal number of edges and tetrahedra in its triangulation. (Purcell, p. 79))
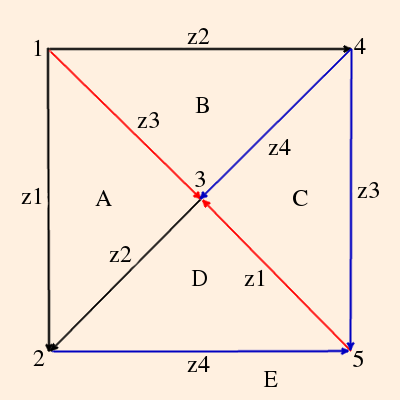
The vertex invariant of a vertex of a Euclidean triangle in the complex plane is the ratio of the adjacent sides. Labeling the vertices clockwise,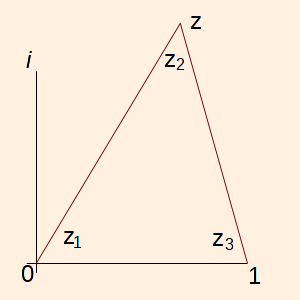
- z1 = z / 1
- z2 = (z - 1) / z
- z3 = 1 / (1 - z)
Note that z1 z2 z3 = -1.
The gluing consistency conditions may be obtained by multiplying the vertex invariants for each edge:
- red: z12 z2 w12 w2 ≡ 1
- blue: z2 z32 w2 w32 ≡ 1
w (w - 1) z (z - 1) ≡ 1.
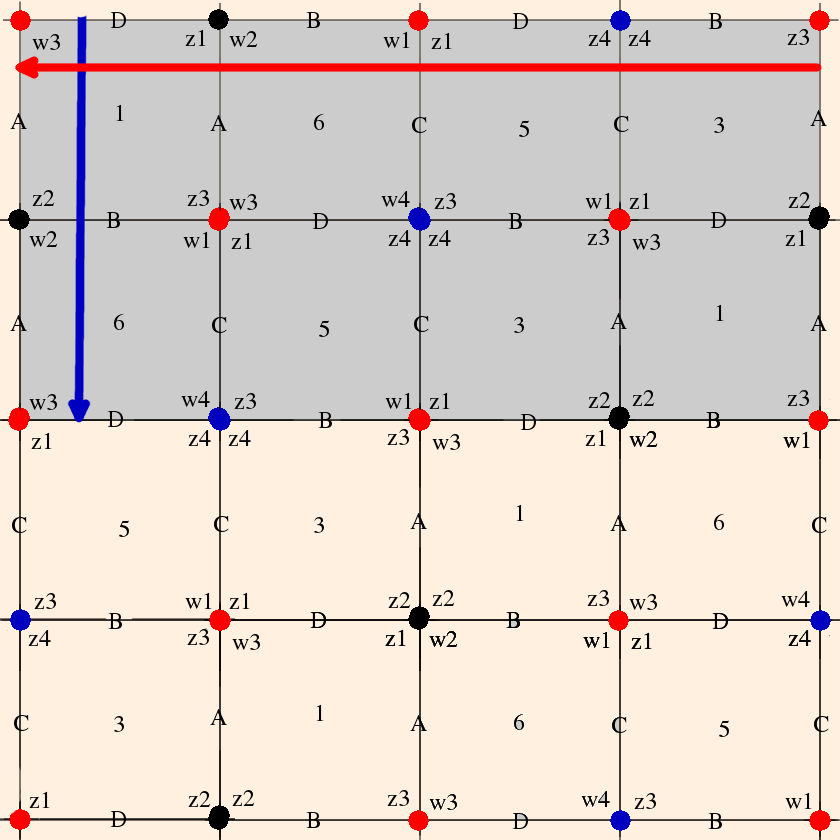
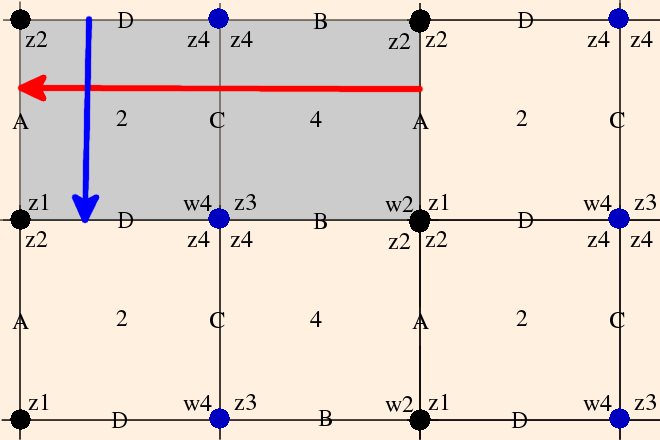
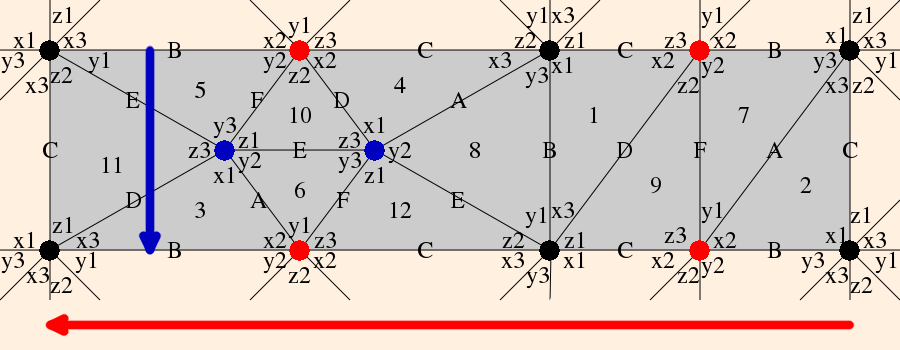
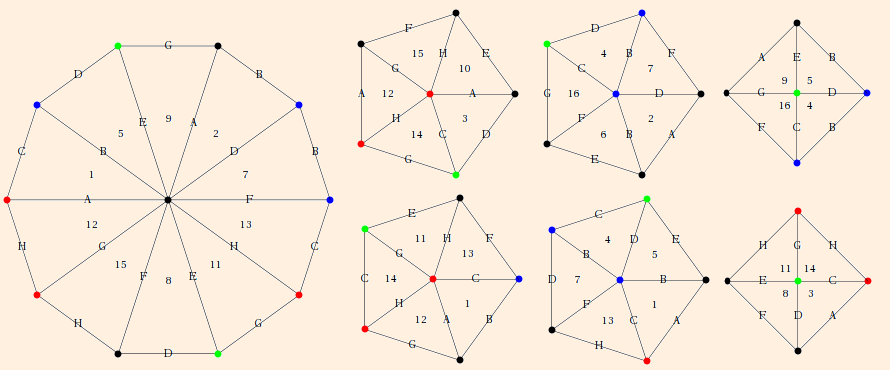
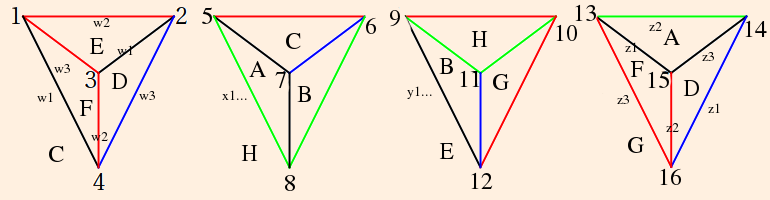
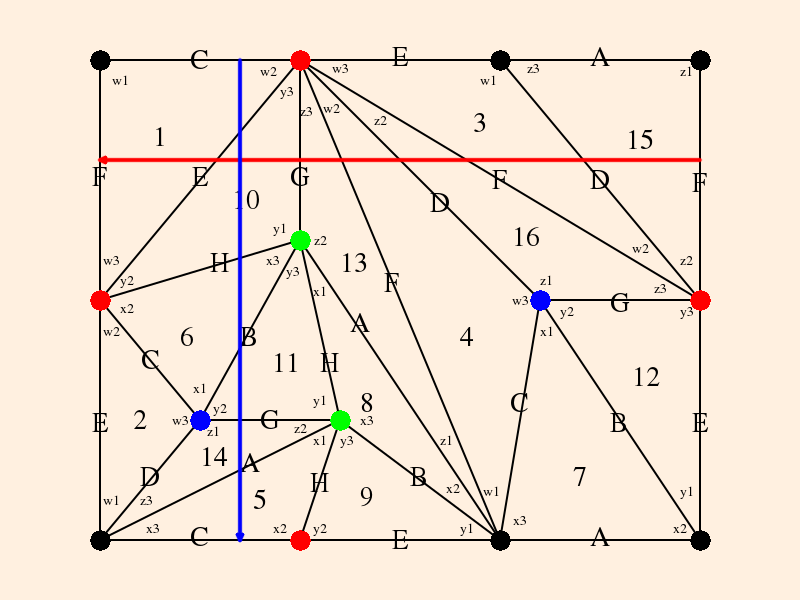
When these conditions are met, the link of the vertex is Euclidean and the manifold is (almost) complete. By considering the neighborhood of the removed vertex, we see that the boundary is a torus (the grayed area is a fundamental domain for the torus):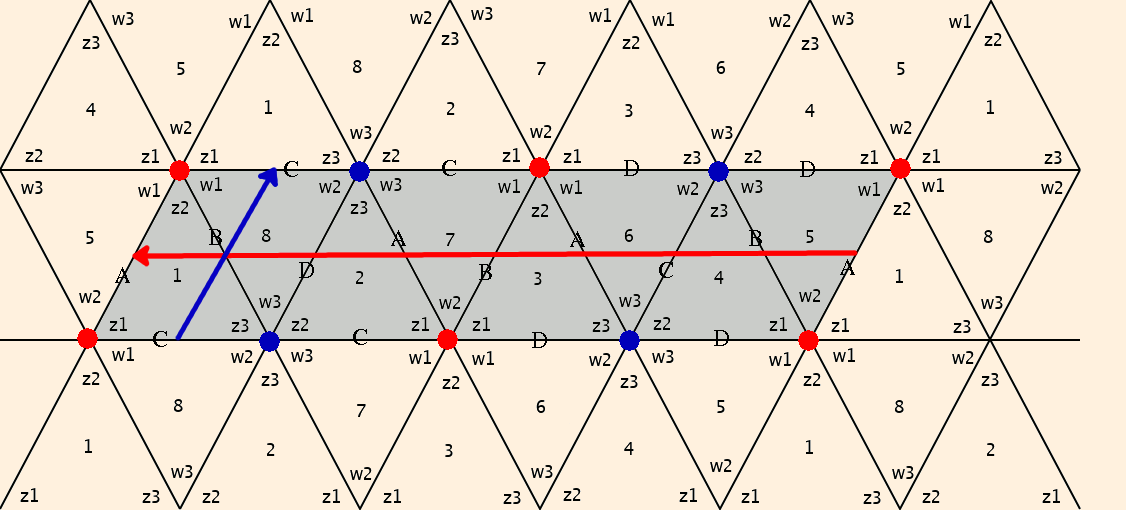
Here, the numbers indicate the vertices, the vertex invariants are labeled, and each triangle represents the link of its associated vertex. The red and blue dots represent the two edges (compare the consistency conditions). Note that the vertex invariants must be in cyclic order in each link, and link edges must share a face; for instance, going from z1 to z2 around vertex 1 you pass through face A; you must therefore pass through that same face when going from w1 to w2 around vertex 5.
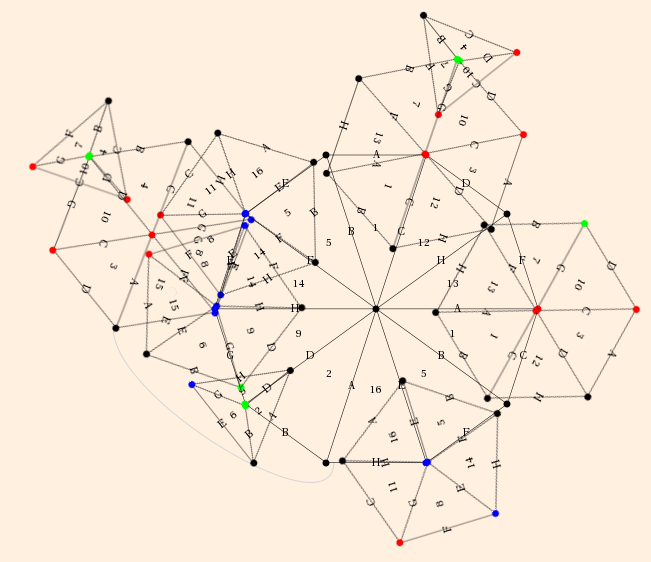
Let's take note of the fact that in the cusp neighborhood diagram, vertices now are faces, edges are now vertices (hubs), and faces are now edges. The hub valences will dictate much of the topology of the neighborhood.
Suppose the holonomy is H(l) for the longitude of the torus, and H(m) is the holonomy for the meridian of the torus. Consider transporting a vector between the red edges adjacent to vertex 1 (say, pointing up), along the red arrow (longitude) to its corresponding position at the end of the red arrow (again, pointing up). Rotation across a vertex invariant zi in a counterclockwise direction introduces a factor of zi in the numerator, while rotating across zi in a clockwise direction introduces a factor of zi in the denominator. We obtain:
- dH(l) / dl = w2 / z3 * w3 / z2 * w2 / z3 * w3 / z2
= z12 / w12 (after multiplying by z12z22z32 / w12w22w32 ≡ 1), and (for a meridianal vector pointing left along the blue arrow)
- dH(m) / dm = w1 / z3.
In addition, completeness imposes two other conditions: dH(l)/dl and dH(m)/dm must both equal one (the holonomy must be trivial). The first condition tells us that z=w; the second determines z:
z (1 - z) ≡ 1
Since we require solutions such that Im(z) > 0 (Im(w) > 0) (all dihedral angles positive and ≤ π), z = (-1)1/3 = eiπ/3 (the dihedral angles are all equal to π/3). Notes that this solution also satisfies the completeness conditions. We could have also seen this from the fact that the tetrahedra are ideal, and all ideal vertices have Euclidean links.Remember that the vertices 1 through 8 are identified, and that vertex is ideal, and so lies on the sphere at ∞. Tangent to that vertex is a family of Euclidean spheres called horospheres. They form the neighborhood of the cusp at the ideal vertex. All geodesics ending at the vertex are normal to the horospheres.
Since the vertex neighborhood (the cusp torus) is Euclidean, the ratio of the lengths of the longitude to the meridian is simply 4. The acute angle is 60 degrees, so the homological cusp shape isHere is an image of the figure 8 knot complement horospheres from SnapPy:

Here is the same image overlaid with the limit set above:

The void areas in the limit set are centered on the parabolic fixed points at the center of each horosphere.
4 eπ i / 3 = 2 + 3.464102 i.
(Adams et. al.)This agrees with SnapPy +2. In fact, out of SnapPy 2.8's CensusKnots with a single cusp, only 81 out of 1267 did not differ by a real integer when choosing the shortest lengths.
The figure 8 knot complement is H3 / G, where G is generated by
a(z) = z / (z + 1),
and G is doubly degenerate. (Marden, section 3.14)(a = ((1,0),(1,1)) and is therefore parabolic.)
b(z) = z + ei π/3,(b = ((1,ei π/3),(0,1)) and is also parabolic.)
a = {{1,1},{0,1}} and b = {{1,0},{-σ,1}}, where σ is a primitive cube root of 1, is also a representation of π1 of the figure 8 knot complement. ((Purcell, p. 101)
This means the figure 8 knot complement is located in the Riley slice at λ = -σ/2 = 0.25 + √3 i / 4. (Koehler (2020))
- The Whitehead link (denoted "L5a1") complement is constructed in almost the same fashion:
front:

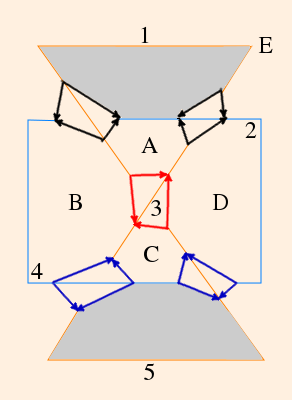
 back:
back:
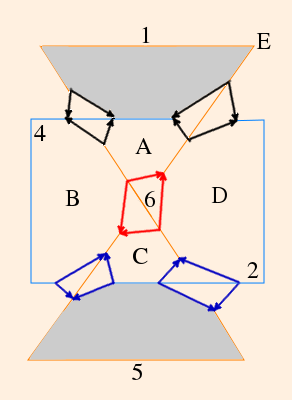
What we end up with, however, is two pyramids which join at face "E" to form an octahedron:
The faces with labels near vertices 3 and 6 are "behind" the octahedron; the others are in front.
Since the link of each vertex is a square, the old rules and relationships concerning zi no longer hold. The rules for constructing the cusp neighborhoods are always good, however.
Because the vertices lie on the S2 at ∞, they are all ideal, so all the vertex invariants are equal to eiπ/2. But we proceed as before.
Comparing faces we find that
- vertices 1, 3, 5 and 6 are identified, and
- vertices 2 and 4 are identified.
Note that we have 2 pyramids, 5 faces and 3 edges. The gluing conditions are:
- black: z1 z22 w2 ≡ 1
- red: z1 z3 w1 w3 ≡ 1
- blue: z3 z42 w4 ≡ 1
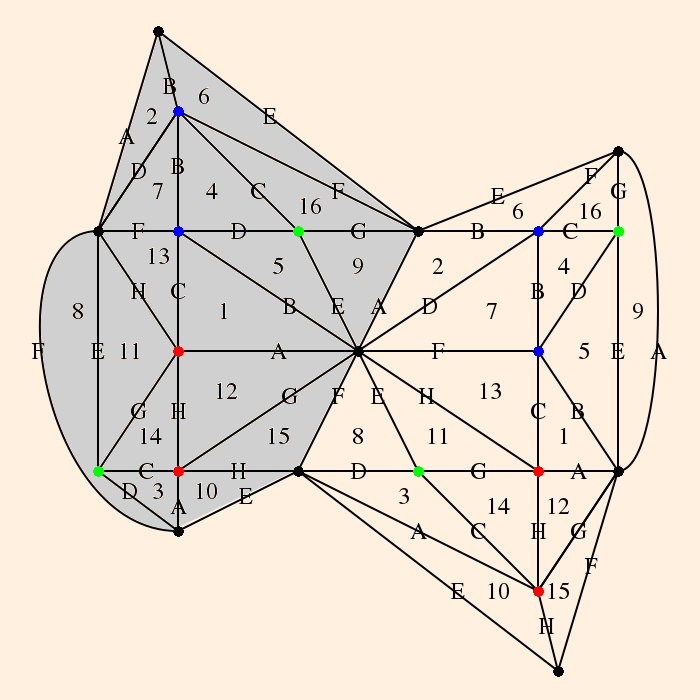
The cusp neighborhoods (one for each component of the link) are:
The holonomies for the first cusp are (following the arrows, as before, starting with a vector pointing up and a vector pointing to the left, respectively)
- dH(l) / dl = z1 z22 z32 w1 w3 w4 ≡ 1;
- dH(m) / dm = z1 z2 z32 z4 w12 w4 ≡ 1.
For the second cusp they are (from top to bottom and right to left)
- dH(l) / dl = z1 z3 w2 w4 ≡ 1;
- dH(m) / dm = z42 w42 ≡ 1.
The (already known) solution zi = wi = eiπ/2 satisfies all of these relationships.
Here are the SnapPy horospheres for the Whitehead link, overlaid with its limit set:

The limit set was generated by
- a = ((i, -i), (-1-i, 1))
- b = ((-1+2i, -2i), (-1-i, 1))
- The Borromean Rings (notated "L6a4") are 3 linked S1 such that cutting any one unlinks the other two.
Here is the front side:
On the octahedron drawing, faces A, D, G and H are "behind" the octahedron, and faces B, C, E and F are in front.
The back side of the rings looks like this:
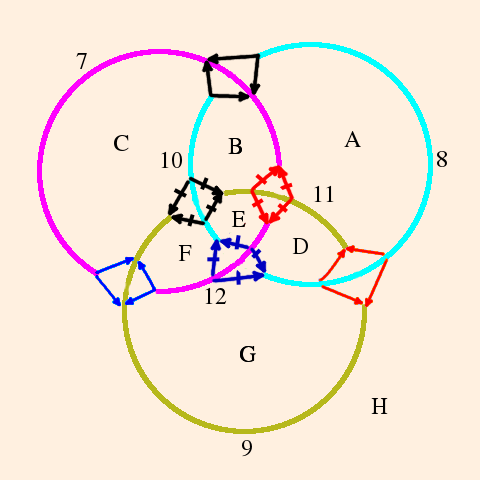
Note that all of the edges have been changed; this was done to avoid a trivial identification between the two octahedra.
The important thing is that each face must have the same edge types adjacent in back as in front.
Faces A, D, G and H are "behind" the octahedron, and faces B, C, E and F are in front.
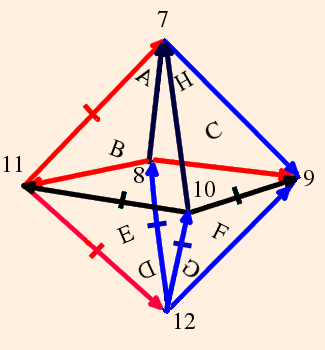
So we have 2 octahedra, 8 faces and 6 edges. The link of each vertex is once again a square. In order to assign vertex invariants, it helps to unfold the octahedra:
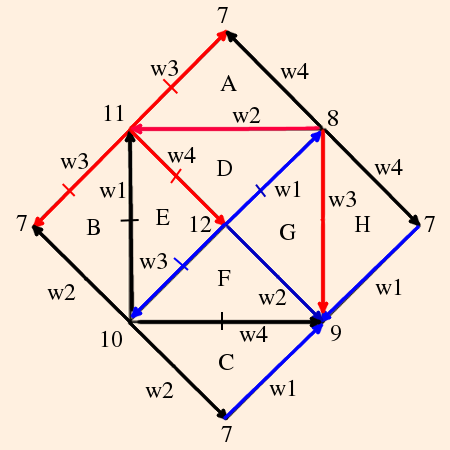
The gluing conditions are:
- black: z1 z3 w2 w4 ≡ 1
- hashed black: z2 z3 w1 w4 ≡ 1
- red: z1 z4 w2 w3 ≡ 1
- hashed red: z3 z4 w3 w4 ≡ 1
- blue: z1 z2 w1 w2 ≡ 1
- hashed blue: z2 z4 w1 w3 ≡ 1
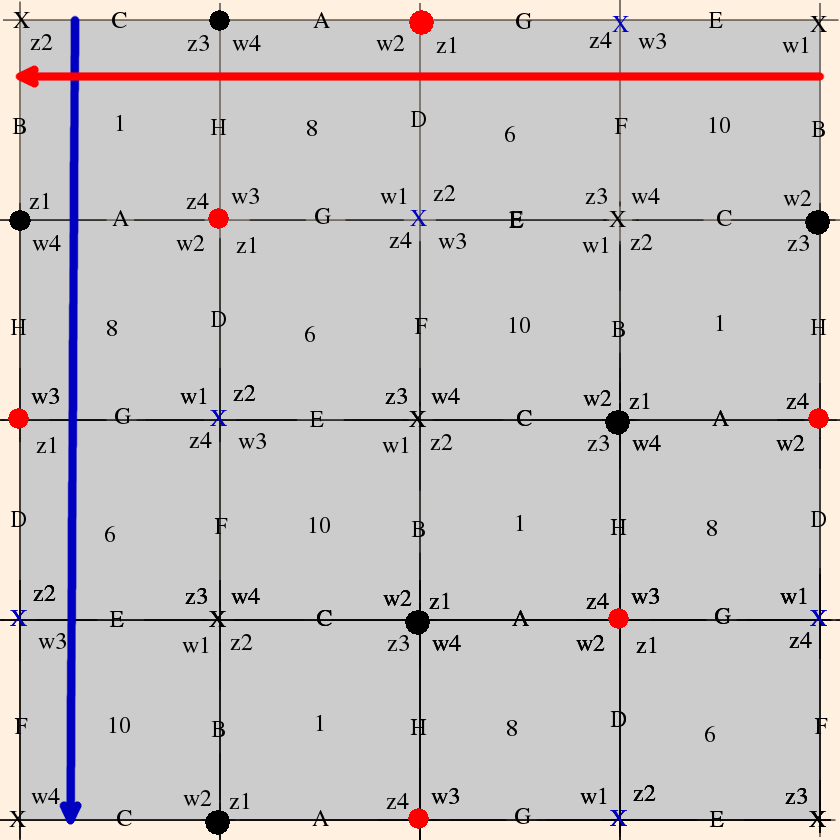
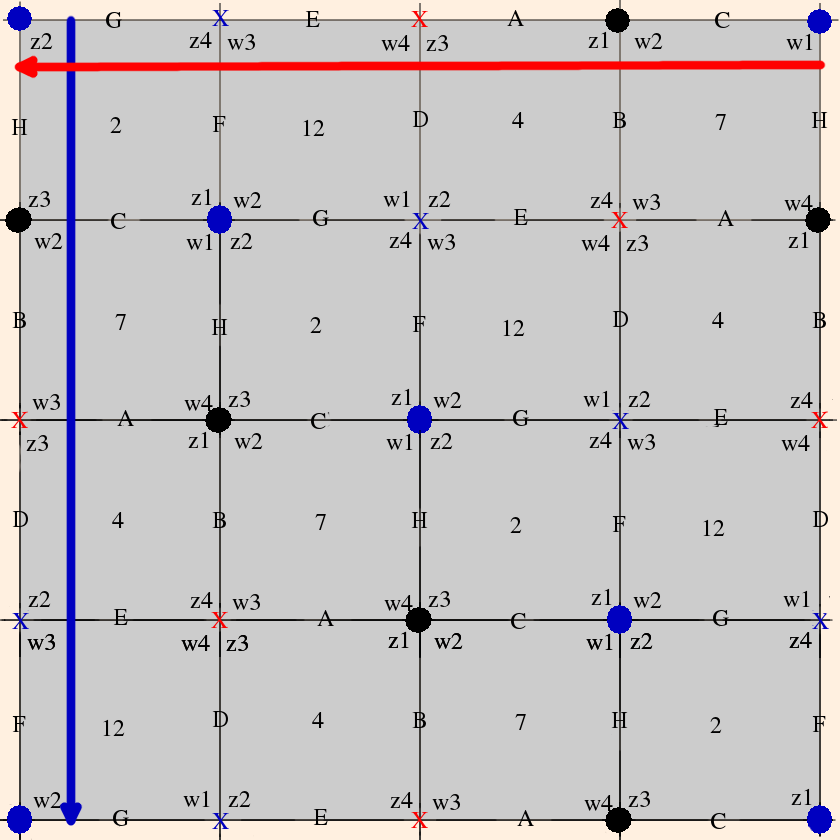
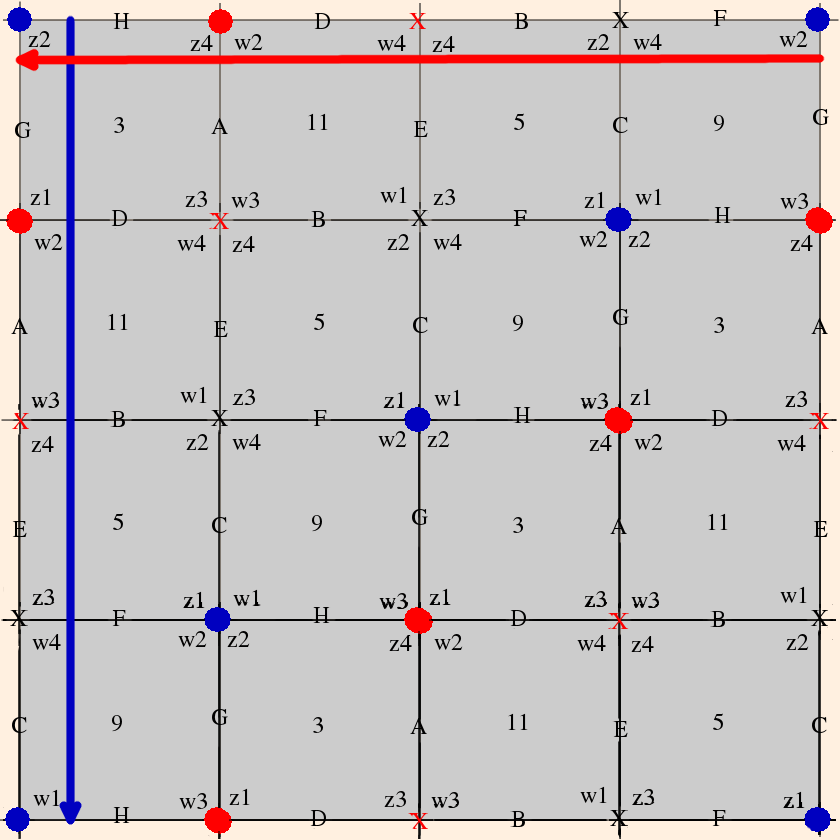
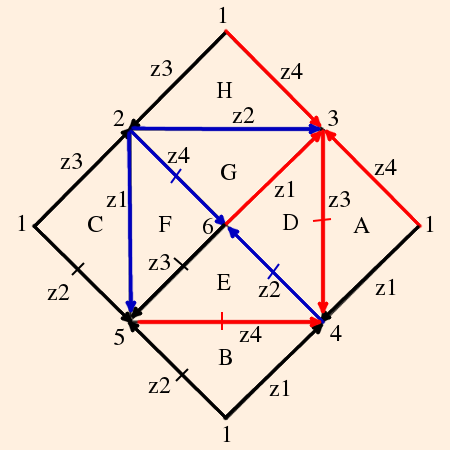
From the cusp neighborhoods, we see that
- vertices 1, 6, 8 and 10 are identified;
- vertices 2, 4, 7 and 12 are identified; and
- vertices 3, 5, 9 and 11 are identified.
- dH(l) / dl = w2 w4 z3 z2 w1 w3 z4 z1 ≡ 1;
- dH(m) / dm = z3 z4 w2 w1
z4 z3 w1 w2 ≡ 1, or
z32 z42 w12 w22 ≡ 1.
For the second cusp they are (from top to bottom and right to left)
- dH(l) / dl = w4 w3 z4 z2 w1 w2 z1 z3 ≡ 1 (same as the first cusp);
- dH(m) / dm = z4 z1 w1 w4 z1 z4
w4 w1 ≡ 1, or
z12 z42 w12 w42 ≡ 1.
For the third cusp they are (again, from top to bottom and right to left)
- dH(l) / dl = w3 w1 z1 z3 w1 w3
z3 z1 ≡ 1, or
z12 z32 w12 w32 ≡ 1;
- dH(m) / dm = z4 z3 w4 w1 z2 z1 w2 w3 ≡ 1 (same as the other two longitudinal holonomies).
As we expected, because each vertex is ideal and has a square link, the solution is again zi = wi = eiπ/2.
- I relied on Thurston's Notes extensively for the above. Let's look at the simplest hyperbolic knot after the
figure 8 knot, the 5_2 knot:
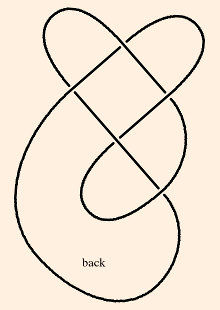
I would have liked to do this one solo, but the edge coloring and face assignment, not to mention the triangulation, seemed unfathomable. Looking for guidance, I found Takahashi's paper which, though he changes notation from one figure to the next, was extremely helpful.
One of the reasons I find this stuff so fascinating is that it forces me to widen my range of options into ideas which to me seem unintuitive. For instance, it seemed logical to me that vertices could only be identified if they connected the same edge types. I also expected that the face assignments for the front and back should mirror each other. I knew that face assignments to tetrahedra were fair game as long as the edges matched, but I had naively assumed that when Thurston said that the zi should cyclical, he meant the tetrahedra as well as the cusp neighborhood.
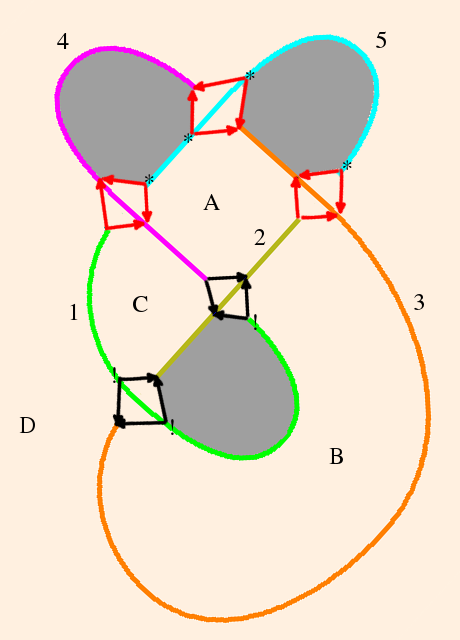
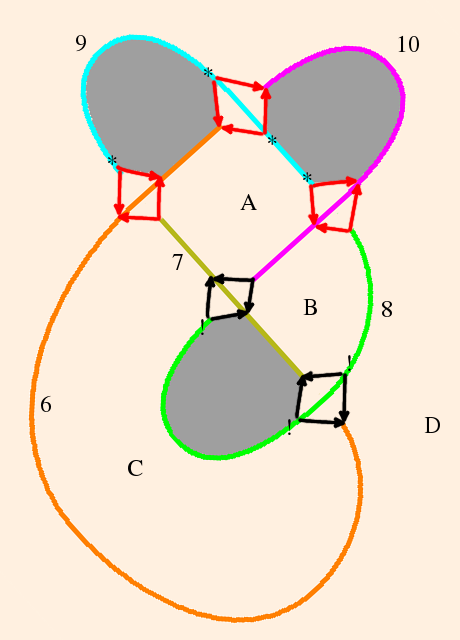
Note that in each diagram, the arrows (edges) with an asterisk at their base must all be the same color;
similarly, those marked with an exclamation point at their base must all be the same color.
Note also that faces with the same label must be bounded by the same edges types.Below on the left, we have two planar graphs consisting each of two triangles (B and C) and two quadrilaterals (A and D). These do not a polyhedron make.
There are several options here:
If, however, we glue the faces D together with a twist (vertices 1 to 6, 4 to 9, etc.) and triangulate the remaining quadrilaterals, we obtain the graph on the right:- glue faces A together (vertices 2 to 9, 4 to 10, etc.) and add edge 3-4; this would create 2 tetrahedra with 3 edges;
- glue face A to face D and vise versa (vertices 1 to 7, 3 to 10, etc.) and add edges 2-8, 2-5 and 3-4; this would create 4 tetrahedra with 3 edges;
- glue faces D together (vertices 1 to 8, 4 to 6, etc.) and add edges 3-4 and 5-7; this does create 3 tetrahedra with 3 edges, but the gluing conditions are wrong (this is where I really need help - how do you know without having a solution at hand?).
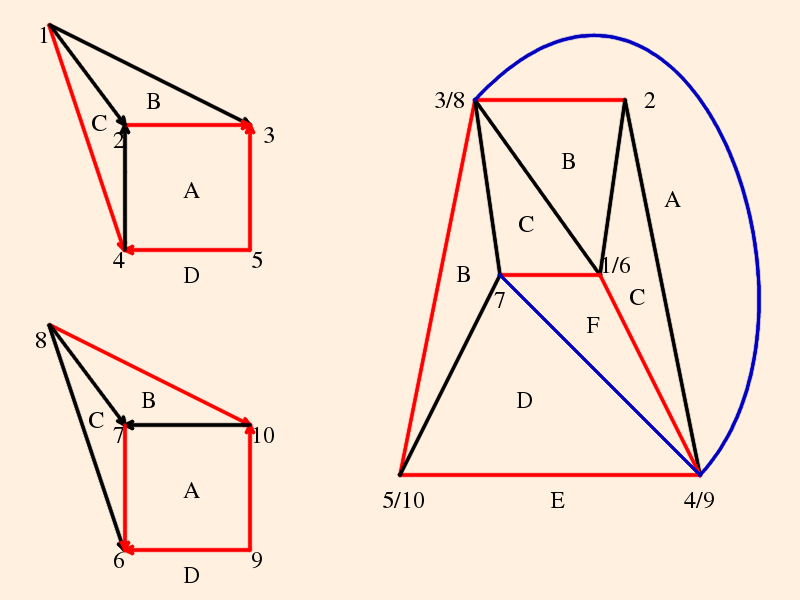
which can be decomposed into three tetrahedra (note that the edge 3-4 creates faces 1-3-4, which is face D, 3-4-7, which is face E and 3-4-5, which is face F; 4-5-7 was color matched to face A, since we already had two D faces):
We renumber the vertices in preparation for determining the cusp neighborhood, and add vertex invariants:
The gluing conditions are then:
- black: x1 x32 y1 y3 z1 z2 ≡ 1;
- red: x22 y1 y2 z2 z3 ≡ 1; and
- blue: x1 y2 y3 z1 z3 ≡ 1.
- dH(l) / dl = y1 / x3 * x3 / z2 * x1 / y3 *
y3 / z2 / z2 ≡ 1, or
x1 y1 ≡ z23;
- dH(m) / dm = z3 / (x3 y1) ≡ 1.
- x = 0.12256116687665364 + 0.7448617666197441 i
- y = 0.6623589786223728 + 0.5622795120623012 i
- z = 0.7849201454990264 + 1.3071412786820453 i
- m / Sin(Arg(x2)) == a / Sin(Arg(x3)),
- m / Sin(Arg(z1)) == b / Sin(Arg(z2)),
- m / Sin(Arg(y2)) == e / Sin(Arg(y3)),
- e / Sin(Arg(z3)) == c / Sin(Arg(z1)),
- m / Sin(Arg(z3)) == f / Sin(Arg(z2)) and
- f / Sin(Arg(x2)) == d / Sin(Arg(x1)).
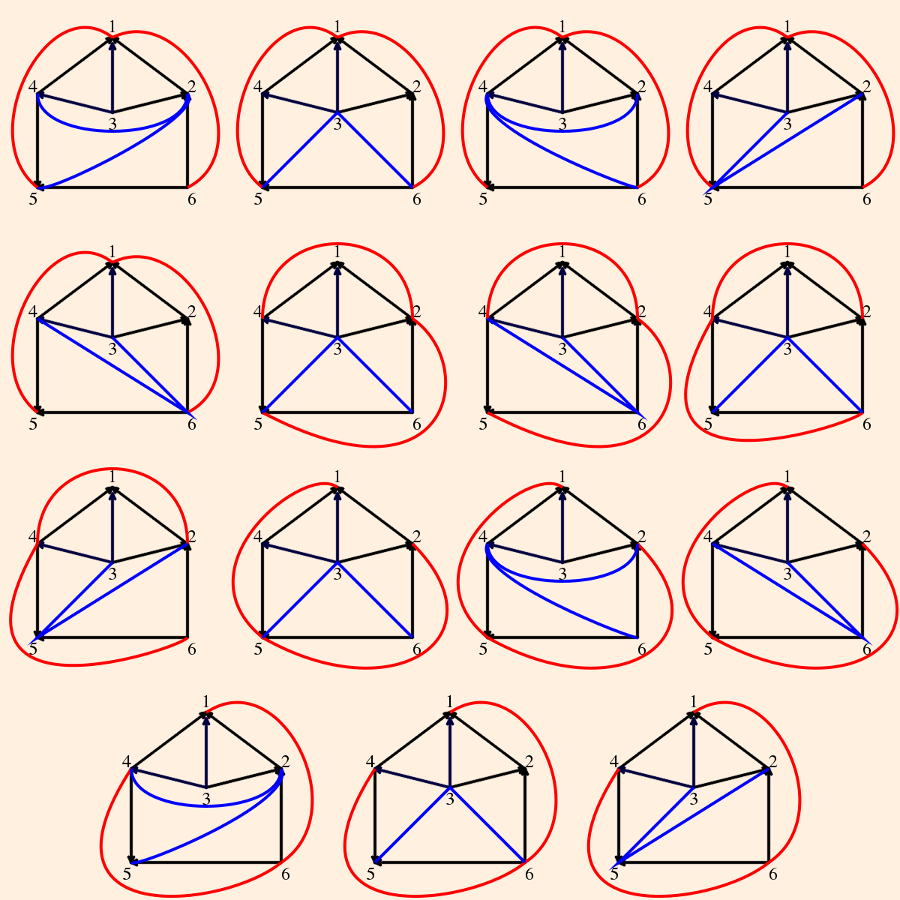
- The next most complicated hyperbolic knot is the 6_1 (or Stevedore) knot:
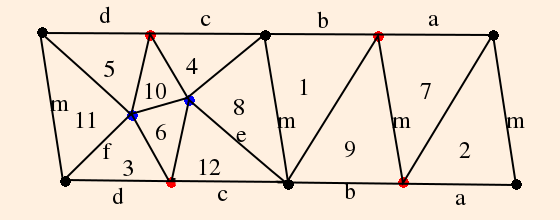
We know that we will have (eventually) 4 tetrahedra and 4 edges because we have 2 triangular faces and 2 pentagonal faces, and each of the latter will be divided into 3 triangular faces by 2 additional edges each, giving 8 faces. Comparing faces, we see that
- A: {a, a, b} ≡ {v, v, x}, which tells us that a≡v and b≡x (possibly a≡v≡b≡x);
- B: {a, d, e} ≡ {v, y, z}, which tells us that {d,e}≡{y,z};
- C: {a, b, c, c, e} ≡ {v, z, w, w, x}, which tells us that c≡w and e≡z (possibly c≡w≡e≡z);
- D: {b, b, c, c, d} ≡ {w, w, x, x, y}, which tells us that d≡y.
We have identified 5 edge classes, where all the members in a class must have the same type (color). In addition, there are 4 new edges which will be introduced when we triangulate the pentagons, each of which may have a different color. With 4 allowable edge types, there are then 49 = 262,144 possible color assignments. Since actual color is not important, this number overcounts the number of different edge assignments by a factor of 4! = 24. However, when programming this problem it is far easier to simply try them all and sort it out afterwards.
There are 15 ways to triangulate the two pentagons:
If we demand that at least one front-side polygon be identified with one back-side polygon, but allow any arrangement of vertex identifications, there are 320 possible outcomes of the identification.
Finally, one must assign vertex invariants for each tetrahedron in either a clockwise or a counterclockwise direction. For 4 tetrahedra, there are 16 possible ways to do this (all clockwise, one counterclockwise, two counterclockwise, three counterclockwise or all counterclockwise: 1+4+6+4+1 = 16). This gives a total of 19,000,197,120 possibilities.
Most of the possibilities will not be useful; in order to form a cusp neighborhood,
- every edge type must have a complete hub,
- for each complete hub, every "spoke" of a different edge type must be able to be "welded" to other complete hubs, and
- all of the complete hubs taken together must contain all vertices.
I use the term "weld" to avoid confusion with the traditional term gluing.
Having prototyped the computation in Mathematica, I wrote a C program to do this analysis. For each successful triangulation, the program outputs the graph after polygon identification and the sets of tetrahedra, along with metadata identifying the triangulation (color permutation, identification rule, added edges and vertex assignments). By specifying the metadata and extended debug options, the program can provide a complete list of the hubs it constructed for that triangulation.Note that this does not guarantee a complete cusp neighborhood; there can still be inconsistent overlap of adjacent hubs.
Guided by the examples above, I selected program options so that adjacent vertices in any hub must be from different tetrahedra. After about 74 minutes on a 3 GHz Intel CPU, it produced 16 unique sets of tetrahedra, with edge multiplicities ranging from 3 to 12, and face multiplicities ranging from 2 to 4.
Focusing on triangulations with 8 unique faces, I found the following:
- These graphs
with this set of tetrahedra (drawn now by a Mathematica program; all vertex invariants follow the pattern in 1-2-3-4):
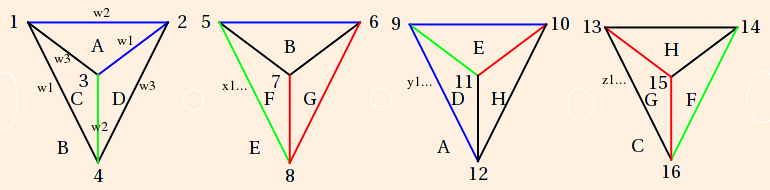
Another Mathematica program produced the following hub graphs:
from which this cusp neighborhood was constructed:
The gluing relations and the usual longitudinal and meridianal holonomies produced the following consistency equations:
- w1 w32 x1 x3 y2 y3 z12 z2 ≡ 1,
- x2 x3 y1 z2 z3 ≡ 1,
- w1 w2 x2 y1 y2 ≡ 1,
- w2 x1 y3 z3 ≡ 1,
- z2 y2 z1 x1 w3 w3 ≡ w2 y1 and
- x1 y2 w3 ≡ z3.
- w = 0.404256+0.254426i,
- x = 0.419643+0.606291i,
- y = 0.228155+1.115143i and
- z = 1.419643+0.606291i,
(0.352201 + 1.72143 i) matches m036 (again using the acute angle).
- These graphs
and this set of tetrahedra (as above):
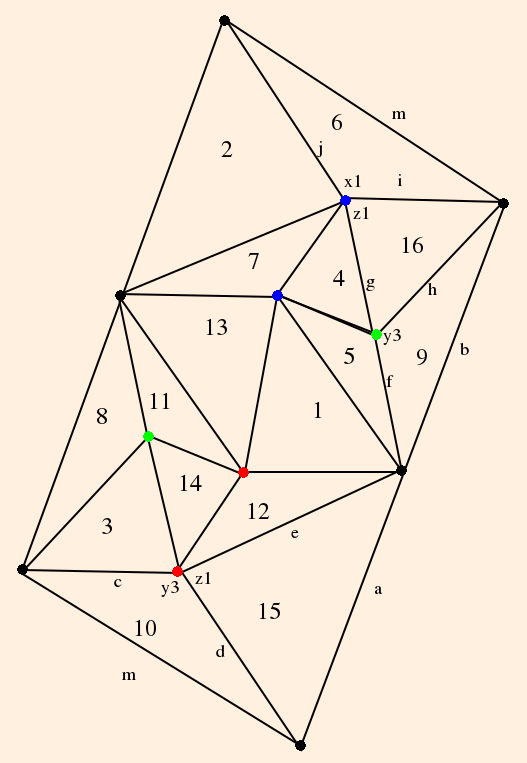
which yielded the hub graphs:
- w1 w2 x22 x3 y12 y2 z2 z3 ≡ 1,
- w3 y2 y3 z1 z2 ≡ 1,
- w1 w3 x1 x3 z1 ≡ 1,
- w2 x1 y3 z3 ≡ 1,
- y2 w3 w1 ≡ x1 x3 and
- x3 z2 x2 w2 y1 y1 ≡ y3 z1.
- w = 0.823899 + 0.860717i,
- x = -0.771845 + 1.11514i,
- y = 1.41964 + 0.606291i and
- z = 0.228155 + 1.11514i,
from which this cusp neighborhood was constructed:
The gluing relations and the usual longitudinal and meridianal holonomies produced the following consistency equations:
which yields a volume of 3.17729 and a Chern-Simons invariant (below) of 0.28427 (equivalent to -0.21573). The geometrically precise cusp neighborhood is
The cusp shape is 0.352201 + 1.72143i so this also seems to be census manifold m036.
- These graphs

and this set of tetrahedra (as above; original vertices were 1-2-3-5, 1-3-4-5, 2-3-5-6 and 2-5-6-9):
which yielded the hub graphs:
- w1 w2 x2 x3 y1 y22 z1 z32 ≡ 1,
- w3 x1 x2 z1 z2 ≡ 1,
- w1 x1 y3 ≡ 1,
- w2 w3 x3 y1 y3 z2 ≡ 1,
- x3 w1 y2 x2 y1 ≡ z22 and
- w3 z1 ≡ x3 z1 y1 x3.
- w = 0.21508 +1.30714i,
- x = -0.662359+0.56228i,
- y = 1.87744+0.744862i and
- z = 0.337641+0.56228i,
- These graphs
and this set of tetrahedra (as above; original vertices were 1-2-3-5, 1-2-5-6, 1-3-4-5 and 3-4-5-8):
which yielded the hub graphs:
- w1 w2 x22 x3 y2 y3 z12 z2 ≡ 1,
- w3 y1 y2 z2 z3 ≡ 1,
- w1 w3 x1 x3 y1 ≡ 1,
- w2 x1 y3 z3 ≡ 1,
- x3 y1 y2 ≡ z2 z3 and
- z2 w1 z1 y3 x22 ≡ x1 w3.
- w = 0.823899+0.860717i,
- x = -0.771845+1.115143i,
- y = 0.228155+1.115143i and
- z = 1.419643+0.606291i,
- w = 1.6623589786223791 + 0.5622795120623022i,
- x = -0.8774388331233477 + 0.7448617666197448i,
- y = 0.6623589786223767 + 0.562279512062306i and
- z = 0.7849201454990266 + 1.3071412786820455i,
- w12 x2 x3 y1 z1 z3 ≡ 1 (black)
- w22 w3 x2 y2 y3 z2 z3 ≡ 1 (red)
- w3 x1 y2 z1 ≡ 1 (blue)
- x1 x3 y1 y3 z2 ≡ 1 (green)
- z2 w2 / (z2 w2 z3 y3) w3 ≡ 1 (longitude)
- w2 / (y2 x2) w3 / (z3 x3) ≡ 1 (meridian)
- w = 0.8951233822596538 + 1.5524918200618698 i
- x = -1.5041083641507362 + 1.226851637746575 i
- y = 0.1738497938368023 + 1.0690718998757216 i
- z = 0.04331543043531902 + 0.6411996580569997 i
- (1/z3) y1 /(x2 w2 y3) z1/w2 ≡ 1 (longitude)
- (z3 /y2) (x2/z3) w2 ≡ 1 (meridian)
- f / Sin(Arg(w1)) == b / Sin(Arg(w3))
- b / Sin(Arg(z1)) == c / Sin(Arg(z3))
- c / Sin(Arg(w2)) == e / Sin(Arg(w1))
- c / Sin(Arg(w2)) == d / Sin(Arg(w3))
- d / Sin(Arg(x1)) == g / Sin(Arg(x3))
- g / Sin(Arg(y1)) == h / Sin(Arg(y2))
- a / Sin(Arg(y3)) == h / Sin(Arg(y2))
- h / Sin(Arg(x1)) == k / Sin(Arg(x3))
- k / Sin(Arg(z3)) == l / Sin(Arg(z2))
The holonomies are (following the arrows, as before, starting with a vector pointing up and a vector pointing to the left, respectively)
The solution is
Using the Law of Sines (for a Euclidean triangle, if a, b and c are the lengths of the sides and α, β and γ are the opposite angles, a / Sin(α) = b / Sin(β) = c / Sin(γ)), we find that
This gives, for the ratio of the lengths of the longitude to the meridian,
L/M = (a + b + c + d) / m =
Using the acute angle θ = Arg(x3) + Arg(y3), we multiply the ratio times ei θ and find the homological cusp shape to be -0.490245 + 2.97945 i. This agrees with SnapPy's result.Csc(Arg(y2)) Csc(Arg(z3)) Sin(Arg(y3)) Sin(Arg(z1)) + Csc(Arg(z1)) Sin(Arg(z2)) + Csc(Arg(x2)) (Sin(Arg(x3)) + Csc(Arg(z3)) Sin(Arg(x1)) Sin(Arg(z2)))
= 3.01951.
from which this cusp neighborhood was constructed:
The gluing relations and the usual longitudinal and meridianal holonomies produced the following consistency equations:
which yields a volume of 2.82812 - the volume of the 5_2 knot complement! Also the volume of the (-2,3,7) pretzel knot complement. But as its Chern-Simons invariant is 0.236537, in fact it seems to be the (-1,2) Dehn fill of census manifold m206.
Once one has computed the vertex invariants, it is a simple matter of adding up all the interior angles around the perimeter to determine if the corresponding manifold is open or closed (does or does not have a cusp). In this case, the sum is 1440 degrees, corresponding to a 10-sided polygon:
nsides = (Σinterior angles θi) / 180 + 2.
Since our primary interest is in knot complements, which are by definition open, we will ignore closed manifolds in the sequel.(angles measured in degrees)
Oddly enough, it tiles the Euclidean plane.
from which this cusp neighborhood was constructed:
The gluing relations and the usual longitudinal and meridianal holonomies produced the following consistency equations:
which is again m036, with y and z interchanged.
All of the remaining unique triangulations with 8 color-distinct faces were closed or degenerate (the solutions to the gluing and holonomy conditions were real).
I then modified the program to try all possible identifications of one or two of the individual triangles shown in the set of 15 above (adding a third identification found no additional vertex mappings). This increased the number of vertex identification rules to 12,316, and the total number of triangulation attempts to 48,428,482,560. This version found 49 more distinct triangulations. All had positive cyclic orientation of the vertex invariants (as above), and the ones I examined had 8 distinct face types. Unfortunately, all were either closed or degenerate. One, however, is worth comment as a cautionary tale.
I could have sworn this was m015 (volume = 2.82812, Chern-Simons = -0.15320, the same manifold as the 5_2 knot complement); but after checking the interior angles, I found it was an irregular octagon; probably it is m070(1,4), with orientation opposite to SnapPy's.
Having still not discovered a triangulation yielding the volume and Chern-Simons values I was seeking, I decided to try a different tactic.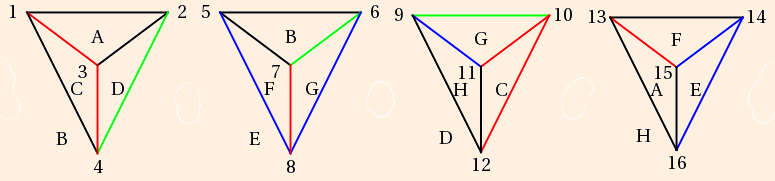
(In this welded hub image, vertices connected by light gray lines or curves are identified.)
First, primarily for the programming exercise, I ran the program to look for 4 identifications of triangles (which found no more vertex mapping rules), and then 5 identifications. That last is a bear; running 24x7 on a water-cooled 24-processor i9-12900K for about a half a year got through somewhat less than half of the possible mappings. Some new mappings were found, but none seemed productive.
So what do you do while waiting for a year-long, basically brute-force, computation to finish? You go back and re-read some of the texts that you only partially understood the first time, hoping to pick up on something that will lead to a more analytical solution to the problem.
And lo and behold, I found it. While working through Thurston's notes, I found in section 3.4, during his discussion of the Borromean Rings, the mention of a gear-like rotation of polygons yielding the correct face-matching. After working through his example closely, I realized there was something that I had never really understood: that there is a method to face-matching where before I had only seen a "trial and error" approach. The only other reference in which I found mention of this was Purcell, exercise 1.5. This method appears to work only for alternating knots. So far, all the knot complements I had worked on were from alternating knots (the figure 8 knot, the Whitehead link complement, the Borromean rings complement and the the 5_2 knot complement). So I re-did them all with gear-motions, and was successful every time (with some slight but easily-corrected missteps along the way). This work will appear in my next (and probably last) monograph.
So I started afresh with 6_1. The first thing to do was add the edges so that every edge pair leads from an overpass to the corresponding underpasses:
As you can see, this restricts us to only two edge colors at this stage (so that the bigons can all be collapsed). Note the gray background to face "C"; after collapsing the bigons, we have
and we see that face "C" is surrounded by faces "A", "B" and "D". When setting up for gear rotation, one shades the faces like a checkerboard, so that any two adjacent faces are shaded differently. For the 6_1 knot, the above shading is the only one in which a shaded face ("C") is adjacent to all unshaded faces (if we shaded any of the others, we would have two shaded faces adjacent).
Rotating the edges of the shaded faces clockwise, and those of the unshaded faces counterclockwise yields the gear-like rotation:
The clockwise rotation of face "C" moves the red edge between vertices 3 and 4 (top left) to the red edge between vertices 8 and 9 (bottom left). Similarly the counterclockwise rotations of the remaining faces. In numbering the vertices on the back side of the knot (bottom left), I simply added 6 to every corresponding vertex on the top side (top left) and identified corresponding vertices of the pentagon "D".
The triangulation of the two pentagons is still a bit of trial and error. This process was aided by a Mathematica program I wrote which identifies groups of 4 unique tetrahedra, given a set of edge colorings. Since we know that 6_1 is built of 4 tetrahedra, we expect 8 faces and 4 edge colorings. After trying all possible triangulations and colorings of the two pentagons, it found groups of tetrahedra with face-type frequencies of {2,2,4,4,4} and {2,2,4,4,2,2}. Choosing to start with the latter because it had more unique face pairs, and taking a hunch that a blue and a green edge would triangulate each pentagon, I tried the edge assignments on the right (above) and obtained the tetrahedra
Renumbering the vertices and adding vertex invariant assignments gives
The anticyclic vertex assignments on the right-most tetrahedron was necessary in able to complete a consistent cusp neighborhood in which every triangle has cyclic vertex invariants:
The shading shows my first attempt at building a complete cusp neighborhood. In the following, that was redrawn within a rectangle in order to compute holonomies:
The gluing relations and holonomy equations are
(curved lines denote angles, bold straight lines denote angles of 180 degrees)
whose geometrically correct neighborhood (within the bounds of my artistic ability) is
I used the first set of solutions to draw this figure, which yielded holonomy equations consistent with that solution:
These solutions give a volume of 3.16396 and a Chern-Simons invariant of 0.155977, both matching the 6_1 knot complement. Using the Law of Sines:
I found that the ratio of the lengths of the longitude to the meridian ((f + e) / (a + l)) was 1.55603. Using the acute angle (86.1353 degrees), I computed a cusp shape of 0.205659 + 0.0281599 i.
I was less than happy to find that SnapPy gives a value of -0.17326172174 + 2.56479863223 i. Knowing now that choice of basis can vary greatly, I found the magnitude of SnapPy's shape was 2.57064. Using my acute angle yielded a cusp shape of 0.339759 + 0.0465217 i. Still not happy. But dividing that last shape by my shape yielded the real number 1.65205, which I take as a confirmation that our cusp shapes are different only in choice of basis.
Geometrization Conjecture
- For the following, X is a connected and simply connected space,
G is the maximal Lie Group of diffeomorphisms
acting transitively on X, H0 is the compact identity component of the isotropy group of G,
and there exists a compact manifold M and a discrete subgroup Γ of G such that
M = X / Γ. (Borisenko, p. 11, 16, 20, 22)
So X is the universal cover of M, and π1(M) = Γ.
Thurston conjectured that every oriented closed prime 3-manifold has a torus decomposition such that its components have one of the following geometric structures. It was proved by Perelman in 2003.X S3 H3 E3 H2 ⊗ R S2 ⊗ R SL(2,R)~ Nil Sol G SO(4) PSL(2,C) R3 ⊗ SO(3) OPS Isom H2 ⊗ Isom E1 OPS SO(3) ⊗ Isom E1 SL(2,R)~ ⊗ R (1) (2) H0 SO(3) SO(3) SO(3) SO(2) SO(2) SO(2) SO(2) {e} ds2 dθ12 + sin(θ1)2 dθ22 + sin(θ1)2 sin(θ2)2 dφ2 (dx2 + dy2 + dz2) / z2 dx2 + dy2 + dz2 dx2 + cosh2x dy2 + dz2 dθ2 + sin(θ)2 dφ2 + dz2 dx2 + dy2 - dz2 dx2 + dy2 + (dz - x dy)2 e2z dx2 + e-2z dy2 + dz2 isometry group O(4) Moeb(E2) O(3) ⊗ R3 Isom(H2) ⊗ R O(3) ⊗ R SL(2,R)~ ⊗ R Nil ⊗ S1 Sol topologically = H2 ⊗ R R3 R3 bundle structure nontrivial S1 over S2 trivial S1 over T2 trivial S1 over surface g > 1 S1 over S2 nontrivial S1 over surface g > 1 nontrivial S1 over T2 nontrivial T2 over S1 Bianchi class IX V, VII I III (none) III, VIII II VI topological invariants e ≠ 0 e = 0 e = 0 e = 0 e ≠ 0 e ≠ 0 R 6 -6 0 -2 2 0 -1/2 -2 Ra bRa b 12 12 0 2 2 0 3/4 4 X "round" T3 H3 H3 ds2 (ra - c2 rb + c2 c3 rc)2 dc12 + (rb - c3 rc)2 / (1 - c22) dc22 + rc2 / (1 - c32) dc32 dx2 + dy2 + dz2 - Σ xi xj dxi dxj / (1 + r2) dr2 + cosh2 r dx2 + sinh2 r dθ2 R 2 c3 (ra - 2 c2 rb + 3 c2 c3 rc) / (rc (-rb + c3 rc) (ra - c2 rb + c2 c3 rc)), < 0 -6 -6 Ra bRa b (2 c32 (ra2 - 3 c2 ra rb + 3 c22 rb2 + 4 c2 c3 ra rc - 8 c22 c3 rb rc + 6 c22 c32 rc2)) / (rc2 (-rb + c3 rc)2 (ra - c2 rb + c2 c3 rc)2), > 0 12 12 (bundle structure Anderson, p. 185)
(curvature invariants from Koehler)- "~" denotes the Universal Cover.
- Nil = 3-dimensional Heisenberg Group (matrices of the form {{1,x,y},{0,1,z},{0,0,1}}).
In the above coordinates, geodesics beginning in the x-y plane lift into the z direction; similarly with the x-z and y-z planes. In the x and z directions, straight lines are geodesics, but not in the y direction.
- Sol = Lie Group with topology R ⊗ R2 such that (t,(x,y))→(etx,e-ty); isotropy group is trivial.
In the above coordinates, geodesics in the x-z or y-z planes stay in those planes; geodesics in the x-y plane do not. Straight lines in the z direction are geodesics, but not in the x or y directions.
- "OPS" denotes Orientation Preserving Subgroup.
- The OPS of Moeb(E2) is PSL(2,C), or Projective SL(2,C) (scalar multiple are identified).
- (1) semidirect product of X with S1, acting by rotations on the quotient of X by its center.
The center of a group is the set of all members which commute with every member of the group.
- (2) extension of X by an automorphism group of order 8.
- e denotes the Euler number of the associated Seifert bundle.
- For T3, the ri parametrize the radii of curvature (with ra > rb + rc and rb > rc) and the ci the cosines of the angles for each of the S1 factors.
d g(t) / dt = -2 Ric(g(t)) + λ(t) g(t)
to approach the singularities and then excise them. To get a feel for how it works, consider Einstein metrics, which are "fixed points" of the flow. For metrics of positive curvature, the flow contracts the metric (to a point in finite time, unless the flow is volume-normalized); for metrics of negative curvature, the flow expands the metric forever. The Ricci Flow preserves isometries since it is diffeomorphism invariant, so the geometric structure is valid arbitrarily close to each singular region. Perelman showed that for an arbitrary 3-manifold, only a finite number of surgeries are required to decompose the manifold into sub-manifolds, each of which has one of the eight geometric structures above. (Anderson, p. 185-9, 191-2)S3, E3, SL(2,R)~, Nil and Sol are unimodular Lie groups. (Scott, p. 464, 468, 470, 478)
Classification
- Any metric of curvature +1 on a spherical 3-manifold is unique up to isometry. (Borisenko, p. 13)
- If M is a smooth manifold, the mapping torus of a diffeomorphism φ: M → M is the manifold
obtained from M ⊗ I by identifying the ends of the cylinder via φ.
Every closed Euclidean 3-manifold is the quotient of T2 ⊗ R by the action of a discrete group Γ:
- T3, the mapping torus of T2 by a translation
- the mapping torus of T2 by the cyclic group of order 2 (C2)
- the mapping torus of T2 by C3, C4 or C6, each of which have two forms distinguished by handedness
- Γ = C2 * C2, acting as rotations around perpendicular axes
The remaining manifolds are not orientable:
- Γ = C2 * C2, acting as glide-reflections in a plane, of index 2 or 4
- Γ = C2 * C2, acting as one screw motion and one reflection, in orthogonal planes,
with two possible spacings
Three of these are Klein bottle bundles over circles. (Weeks (Shape), p. 248)
(Thurston, pp. 159, 233-238)
All 10 closed Euclidean 3-manifolds are finitely covered by the 3-torus. (Scott, p. 448)
- Every elliptic 3-manifold is orientable.
Every elliptic 3-manifold is either a lens space, or the quotient of RP3 by one of the following groups:
- the product of the dihedral group (D2n of a regular n-gon), the tetrahedral group (order 12), the octahedral group (order 24) or the icosahedral group (order 60), with a cyclic group of order relatively prime to the order of the first factor
- a subgroup of index 3 in the product of the tetrahedral group and the cyclic group C3m, m odd
- a subgroup of index 2 in the product C2m ⊗ D2n, n even and m and n relatively prime (D is the dihedral group)
(Thurston, pp. 243, 250)
- There are seven manifolds with S2 ⊗ R structures: S2 ⊗ R and two line bundles over P2 (noncompact); two S2 bundles over S1, P2 ⊗ S1 and P3 # P3 (compact). The latter is the only closed 3-manifold with a geometric structure that is a non-trivial connected sum. (Scott, p. 457)
- M has a Sol structure iff M is either a bundle over S1 with fiber the torus or Klein bottle, or is the union of two twisted I-bundles over the torus or Klein bottle. (Scott, p. 477)
- A closed 3-manifold possesses a geometric structure other than H3 or Sol iff it is a Seifert fiber space.
3-manifolds with geometries E3, H2 ⊗ R or S2 ⊗ R are, up to finite covers, trivial circle bundles over oriented surfaces of genus g, with g = 1, g > 1 or g = 0, respectively.
3-manifolds with geometries S3, SL(2,R)~ or Nil are, up to finite covers, nontrivial circle bundles over oriented surfaces of genus g, with g = 0, g > 1 or g = 1, respectively.
These are also twisted line bundles over S2, H2 and E2, respectively. (Weeks (Shape), p. 253, 254)
A closed 3-manifold possessing Sol geometry is finitely covered by a torus bundle over S1 with holonomy given by a hyperbolic automorphism of T2 (an element of SL(2,Z) with distinct real eigenvalues). (Borisenko, p. 29) - For H3/Γ,
- The minimum dimension of the Teichmuller space of a 3-manifold that admits a hyperbolic structure is -6 χ. (Thurston Notes, p. 88)
- if the manifold is compact, Γ is infinite, has no subgroup of finite index that is abelian, nilpotent or solvable, and does not have a normal, infinite cyclic subgroup;
- if the manifold is noncompact with finite volume, Γ does not have a normal, infinite cyclic subgroup.
(Thurston, pp. 281, 283)
Link Complements
- Every orientable 3-manifold can be obtained from Dehn surgery, cutting a tubular neighborhood of a knot or a link
and gluing it back together with a different identification.
A knot is a simple closed curve.
A knot complement has a cusp along each link component. (Gukov, p. 17)
A link is a union of disjoint knots. - Every compact 3-manifold contains a simple closed curve whose complement admits a noncompact hyperbolic structure of finite volume.
Every noncompact hyperbolic 3-manifold of finite volume can be decomposed into a finite number of ideal hyperbolic tetrahedra. (Callahan et al., p. 321)
The toral cross-section of a cusp can be seen as the open tubular neighborhood of the link components strung along the edges of an ideal tetrahedron. (Weeks)
- The measure of the dihedral angle of an ideal vertex is determined by the link (triangle → π/3, square → π/2, etc.).
Suppose a manifold is constructed from a set of regular ideal polyhedra with
their sides identified in pairs. If the original set had n edges, and the manifold has m, the manifold is complete if n/m times the dihedral
angle = 2π. (Ratcliffe, p. 441)
The link of a cusp (topologically a torus or a Klein bottle) is triangulated by the links of the vertices with appropriate identification.
If the first homotopy group is generated by {xi} and the product of the vertex invariants along each x is Zi, the holonomy along a path aixi is Ziai (implicit summation). If the manifold is complete, the holonomy is trivial.
(Ratcliffe, section 10.5)
- The Dehn filling of a 3-manifold M with torus boundary
is the gluing of a solid torus to the boundary of M.
Dehn fillings are parametrized by H1(∂M, Z) (without regard to orientation). The class parametrizing the
filling is called the slope. (Dunfield, p. 419)
(p,q)-Dehn surgery is a Dehn filling where the meridian wraps p times around the meridian and q times around the longitude (p and q relatively prime, q ≠ 0).
The meridian is the homotopy generator of "shorter" radius (if the torus is filled, it bounds an embedded disc). The longitude is the homotopy generator of "larger" radius (orthogonal to the meridian, intersecting it once).
(p,q) and (-p,-q) surgeries produce the same manifold.(p,q) Dehn surgery on a hyperbolic manifold will produce another hyperbolic manifold except in finitely many (at most 12) cases. (Marden, section 4.10)
The result of Dehn surgery always has a cyclic fundamental group. (Thurston Notes, p. 2)Every 3-manifold can be obtained from Dehn filling of a finite-degree covering space of the Borromean Rings: they are a universal link.
The Whitehead link and the 946 knot:
(Thurston Notes, p. 57, 61) (Thurston, p. 131) (Thurston How..., p. 2569) (Hilden)
are also universal. In fact, every rational knot or link which is atoroidal is universal. (Hilden 2, p. 5)
A rational knot or link is defined as follows. Any rational number can be expressed as a continued fraction:
q / p = 1 / (a1 + 1 / (a2 + ... + 1 / an))
such that- q ≠ 1 mod p (eliminating torus links),
- 1 < q < p / 2,
- n ≥ 2,
- ai > 0,
- a1 ≥ 2 and
- an ≥ 2.
A rational knot (or 2-bridge knot) is formed by alternating horizontal and vertical twists of ai crossings. Its canonical cusp neighborhood will have hubs of valance 2(ai+2). (Sakuma and Weeks, section II.2) (Purcell, section 10.1)
J(2,5) is a twist knot with 2 crossings at the top and 5 crossings at the bottom:
The limit of the J(2,n) knot complements as n→∞ is the Whitehead link complement:
As n→∞, n-twist regions produce complements converging to a link with an unknot circling the former twist region. (Purcell, p. 10)
Oddly, the limit of the double-cusp groups (1,n) as n→∞ is also related to the Whitehead link complement. (Mumford et. al., p. 345)
The J(p,q) twisted knot complements can be obtained by Dehn-filling one of the Borromean ring sisters. (Purcell, p. 132)
- The homology groups of any two knot complements with (p,q) and (p',q') Dehn fillings are the same if p = p'.
(Meyerhoff, p. 47)
π1(knot complement) = Z iff the knot is trivial. (Thurston Notes, p. 2)
- (p,q) is the Dehn surgery invariant of an incomplete manifold M.
For the figure 8 knot complement, the generator of translations in the meridianal direction is (from the link diagram above)
w1 / z3
and the generator of translations in the longitudinal direction is the product of the longitudinal holonomy generator with the square of the meridianal holonomy generator:= w1 (1 - z1)
w22 w32 z14 z22 z32 * (w1 (1 - z1))2
The gluing (completeness) conditions for (p,q) Dehn surgery can then be written as= z12 (1 - z1)2.
(which by the gluing consistency conditions is equal to the result we obtained above.)- p ln|w (1-z)| + 2q ln|z (1-z)| = 0 and
- p arg(w (1-z)) + 2q arg(z(1-z)) = 2π.
where z = z1 is the vertex invariant of the first tetrahedron and w = w1 of the second.
(Ratcliffe, p. 497)
Consider the (1,2) Dehn twist of the figure 8 knot complement. We find z and w by requiring both that the original gluing condition be satisfied and that the product of one meridian traversal and two longitude traversals gives the identity:
- w (1-w) z (1-z) = 1
- w z4 (1-z)5 = 1
There are 16 solutions to these equations; only one satisfies the Dehn surgery gluing conditions and produces zi and wi in the interval (0,π):
- z = -0.243106 + 0.560237i and
- w = 1.35334 + 0.70357i.
Adding all of the interior angles in the torus boundary of the removed vertex, we obtain 1440 degrees. Therefore the torus is described by a 10-sided polygon:|z1| arg(z1) |z2| arg(z2) |z3| arg(z3) |w1| arg(w1) |w2| arg(w2) |w3| arg(w3) 0.61071 113.458 2.23268 42.2824 0.733397 24.2599 1.5253 27.4688 0.516168 35.8646 1.27014 116.667 (arg values in degrees)
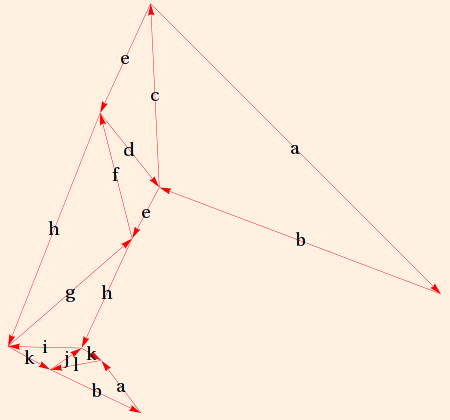
Traversal of a meridian results in the length of a vector increasing by a factor of |w1 (1 - z1)| = 2.07978 and a rotation of arg(w1 (1 - z1)) = 3.20887 degrees counterclockwise; traversal of a longitude results in the length of a vector decreasing by a factor of |z12 (1 - z1)2| = 0.693412 and a rotation of arg(z12 (1 - z1)2) = 178.396 degrees:
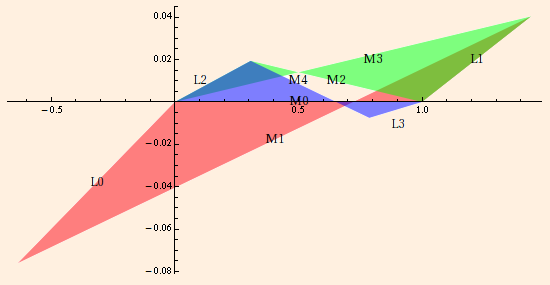
Each "twisted quadrilateral" is a slice of the Dehn-filled cusp, with meridian and longitude edge labeling indicating traversal along two longitudes (red to green and green to blue) and one meridian (blue back to red). Since the manifold is now complete and compact, the red and blue quadrilaterals share a meridian edge (M0): traversal along one meridian and two longitudes brings you back to where you started. (See Weeks.)
- For a square-free integer d > 0:
- PSL(2, Od) is a discrete subgroup of PSL(2, C). Let Γ be a torsion-free subgroup of finite index in PSL(2, Od). Then H3 / Γ is an oriented hyperbolic 3-manifold of finite volume.
- Let D = d if d is 3 mod 4, otherwise D = 4 d.
- Let (-D n) be defined by
- (-D n) = Πprime factors p (-D pi)
- (-D 1) = 1
- (-D 2) = 1 if -D is 1 mod 8, -1 if -D is 5 mod 8
- (-D p) = 0 if p is a factor of D
- (-D p) = 1 if -D is some square mod p, otherwise -1
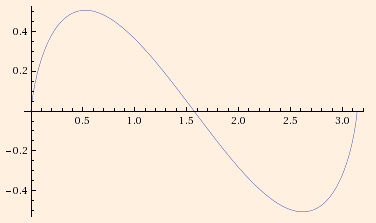
- The Lobachevsky function Π(θ) =
- ∫0θ ln |2 sin u| du
- The volume of H3 / Γ = (D / 12) Σk mod D (-D k) Π(π k / D) times the index of Γ in PSL(2, Od)
The volume of an ideal tetrahedron with dihedral angles α, β and γ (in radians) is Π(α)+Π(β)+Π(γ). (Thurston Notes, pp. 160, 167-169)
- The volume of the figure 8 complement
is 6 Π(π/3) = 2.02988321282... (since an equilateral tetrahedron has dihedral angles of π/3 and there were two tetrahedra).
The volume of the (1,2) Dehn-filled figure 8 complement is
Π(z1) + Π(z2) + Π(z3) + Π(w1) + Π(w2) + Π(w3)
= 1.3985088842...
- The volume of the Whitehead link complement is 8 Π(π/4) (two infinite cones with square link and total angle π each).
The volume of the Borromean Rings complement is twice that of the Whitehead link complement because it is made from two octahedra.
(Thurston Notes, p. 165)
The volume of the 5_2 knot complement is 2.82812208833076.
- For the simple k-linked "closed" chain Ck (in which k S1s are
linked, each to the next and the last to the first), let α =
cos-1 (cos (π/k) / √2) and β = π - 2α.
Then the volume of the complement for k > 1 isv(S3 - Ck) = 2 k (2 Π(β/2) + Π(α + π/k) + Π(α - π/k))
(Thurston Notes, p. 147, 167) - The Weeks manifold, of volume 0.9427, appears to be the unique closed orientable hyperbolic 3-manifold of smallest volume. It is formed by a (2,1) Dehn fill on the "figure 8 sibling" (census manifold m003). (Gabai, Meyerhoff and Milley)
- Let M be a hyperbolic manifold formed by (p,q)-Dehn surgery on a knot complement. The volume of M is less than the volume of the
original (cusped) complement, approaching it in the limit p2 + q2 → ∞.
Here are the volumes produced by (p,q) surgery on the figure 8 knot complement for p,q ≤ 20. Note that for (p,q) = (1,1), (2,1), (3,1) and (4,1), the resulting manifolds are not hyperbolic. The minimum volume (0.981369) is for the (5,1) surgery; the maximum volume shown (2.02326) is for (19,20) surgery; the limiting volume is 2.02988.
- πk > 1 = 0 for any knot complement in S3. (Lickorish, p. 114)
Hyperbolic Manifolds
-
A manifold M is atoroidal if every map of a torus which injects
its fundamental group into M is homotopic to a map to a torus boundary component of M.
An atoroidal manifold contains no essential tori. If a manifold contains an essential torus (or an essential disc), it cannot be hyperbolic (Purcell, pp. 153,4)
Every closed irreducible atoroidal 3-manifold with infinite fundamental group is hyperbolic, (π1 contains no Z⊗Z subgroup).The interior of every compact irreducible atoroidal 3-manifold with boundary is hyperbolic.
(Marden, section 6.3)
- Finite volume manifolds and Mostow Rigidity - If N and N' are 3-manifolds carrying complete hyperbolic metrics of finite volume, and their fundamental groups
are isomorphic, then N and N' are diffeomorphic. This implies volume is a topological invariant.
(Borisenko, p. 13)
Drilling out a geodesic increases the volume of a finite-volume hyperbolic manifold. (Marden, section 4.10)
The volumes of complete hyperbolic manifolds are indexed by countable ordinals in subsets (numbers in parentheses are SnapPy identifiers for orientable manifolds):- volumes of manifolds resulting from Dehn-filling the smallest manifold with 1 cusp (the figure 8 knot complement (m004) or its sibling (m003));
- volumes of manifolds resulting from Dehn-filling the next-smallest manifold with 1 cusp (m006 or m007);
- (continue for all manifolds with 1 cusp);
- volumes of manifolds resulting from Dehn-filling the smallest manifold with 2 cusps (m125 or m129);
- volumes of manifolds resulting from Dehn-filling the next-smallest manifold with 2 cusps (m202 or m203);
- (continue for all manifolds with 2 cusps);
- (etc. for all manifolds with 3, 4, ... cusps).
Geometrically, a cusp is a region isometric to the psuedosphere: the t → ∞ end of the surface of revolution of (x,y) = (t - tanh t, sech t) (parameterized in two dimensions as ds2 = tanh2(u) du2 + sech2(u) dv2, u ∈ [0,∞), v ∈ [0, 2π]):
(Thurston Notes, p. 38, 116, 129, 139) (Thurston How..., p. 2559, 2563)
It is topologically T2 ⊗ [0,∞), has finite surface area (2π) and (interior) volume (π/3), and constant negative curvature; the hyperbolic radian is taken to be unit distance. Note that the surface is not extensible at the t=0 end; the tangent with respect to t is infinite there. The limit surface of the bounding torus is a horosphere (isometric to R2).
For a nonorientable cusp, substitute a Klein bottle for the T2. (Ratcliffe, p. 445)
The first integral betti number of a hyperbolic 3-manifold with cusps must be ≥ the number of cusps. (Callahan et al., p. 329)
Topological invariants of a cusped manifold include:
- the volume of the largest cusp;
- the length of the shortest parabolic translation in the boundary of the maximal cusp;
- the ratio of the complex translations corresponding to the lifts of the meridian and longitude of the link component associated with a cusp: the homological cusp shape;
- the ratio of the lengths of the two shortest linearly independent (complex) parabolic isometric translations: the geometrical cusp shape.
The homological cusp shape of a knot complement M can be heuristically computed from a potential function V for some knots. Consider three of the knots we analyzed above:
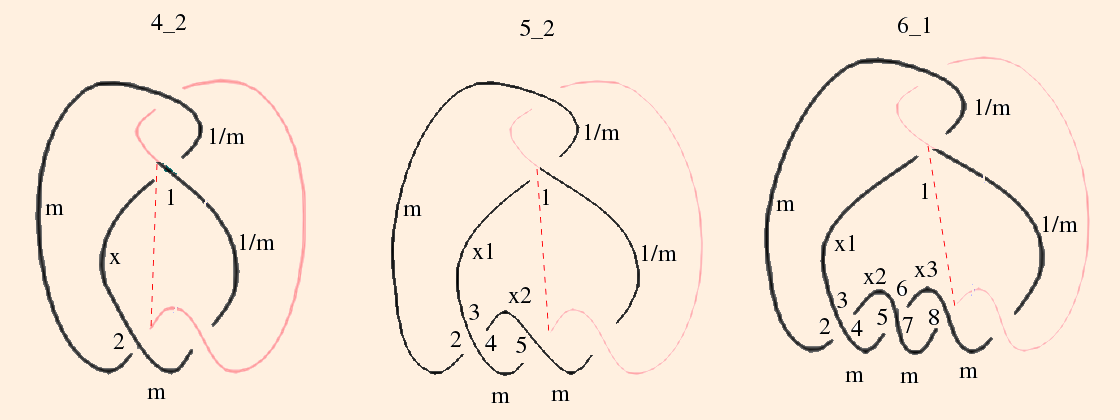
- First we remove one external strand from one overpass to one underpass (the solid pink lines).
- Then we draw a line dividing the removed strand from the rest (the dashed red line).
- Every remaining external strand to the left of the dashed line is labeled with an "m", and every remaining external strand to the right of the dashed line is labeled "1/m".
- The remaining internal strands are labeled xi.
- Each internal angle has been numbered. From the following angle perspectives, the potential function includes a
dilogarithm function (the "Li2") and a term proportional to π2/6:
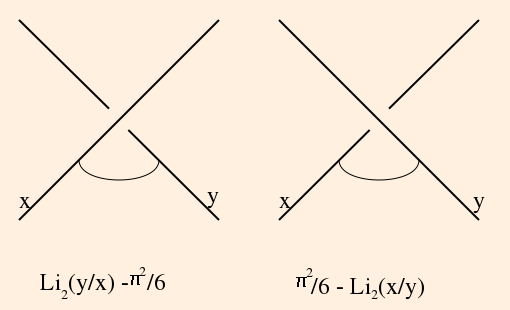
Li2(z) ≡ - ∫0z 1/u ln (1-u) du.
- Add one final term of the form 2 ln(m) (Σall strands ± ln(strand label)), where the sign is,
starting from the removed overpass and continuing along the strands, positive if that labeled strand ends in an overpass,
and negative if it ends in an underpass. Thus the potential functions are:
- 4_2: -Li2(x1/m) + Li2(m/x1) + 2 ln(m) (ln(m) - ln(1/m) + ln(x1) - ln(1/m) + ln(m))
- 5_2: -Li2(m x1) + Li2(m/x1) - Li2(x2/x1) + Li2(m x2) + Li2(1/(m x2)) - π2/6 + 2 ln(m) (ln(1/m) - ln(x1) + ln(1/m) - ln(m) + ln(x2))
- 6_1: -Li2( x1/m) + Li2(m/x1) - Li2(x2/x1) + Li2(m x2) + Li2(1/(m x2)) - Li2(x3/x2) + Li2(m x3) + Li2(1/(m x3)) - π2/3 + 2 ln(m) (-ln(x2) + ln(x1) - ln(1/m) + ln(x3) + ln(m))
- We next find the solutions of the equations xi ∂V/∂xi ≡ 1 for each xi, and evaluated at m = 1. V evaluated at those solutions will include one whose value is cs(M) + Vol(M) i mod π2. We call that the geometric solution.
- Designating m as x0, we then construct matrices
Mi,j = xi xj ∂2 V / ∂xi ∂xj,
where i and j run from 0 through all the x, andNi,j = xi xj ∂2 V / ∂xi ∂xj,
where i and j run from 1 through all the x. - The cusp shape is then ±det(M) / (2 det(N)) at the geometric solution.
Comparing this value to SnapPy's typically requires you tell SnapPy to "set_peripheral_curves("shortest")".
(Many thanks to Sam Nead for pointing this out).
The Chern-Simons invariant is defined modulo 1/2 for orientable manifolds. It changes sign with a change in orientation, so if there is an orientation reversing homomorphism of the manifold, the Chern-Simons invariant must be 0 or 1/4 mod 1/2. It is an obstruction to conformal immersion of the manifold in Euclidean space.
(Callahan et al., p. 329) (Coulson et. al., p.138)
Define
- the Roger's dilogarithm function
Rdf(z) ≡ ½ ln(z) ln(1-z) - ∫0z ln(1-t) / t dt
- R(z;p,q) ≡ Rdf(z) + ½ π i (p ln(1-z) + q ln(z)) - π2/6
- cs(M) = - Σ Ri(z;p,q) + i V(M),
Given a triangulation of a manifold into tetrahedra with vertex invariants {x,y...}i, gluing conditions gi and holonomy conditions hi, first substitute (for each x, y, ...)
- x1 → e±p π i,
- x2 → e±q π i and
- x3 → e± (-1-p-q) π i,
A physicist would say that the xi have acquired a phase
For n tetrahedra, we have n equations ln(gi) = - 2 π i and 2 equations ln(hi) = 0. This is n+2 equations in 3n variables. If by setting the "p"s to zero, these relations provide values for the "q"s, cs(M) should then be real (up to computational precision). If we divide cs(M) by 2 π2, we should arrive at the value given by SnapPy, modulo 1/2.If (α,β) Dehn filling has been performed, cs(M) has an additional term
-i π/2 (γ ln(h1) + δ ln(h2)),
wheredet ((α,β),(γ,δ)) ≡ 1,
the hi are the original holonomy conditions before substitution, and of course, due to the Dehn filling,ln(hi) = 0 becomes ln(α h1) + ln(β h2) = 0.
(Neumann, sections 2, 3, 14 and 15) (Coulson et. al., section 5A)
-
Any complete hyperbolic 3-manifold M is the quotient of H3 by a Kleinian group G, with
π1(M) isomorphic to G.
A Kleinian group is a discrete torsion-free group of isometries of H3 (and is therefore a discrete subgroup of Moeb(E2)), which acts properly discontinuously (the inverse image of any compact set is also compact). The latter implies that a discrete group has a countable number of elements. Kleinian groups are usually taken to be nonelementary - they leave an infinite number of fixed points on the sphere at ∞ (the dimension of the limit set dim(Λ) > 0).
∂M(G) = Ω(G) / G, and is the union of a finite number of hyperbolic Riemann surfaces with at most a finite number of punctures (arising from parabolic fixed points) and conical points (arising from elliptic fixed points). If g is the genus of the surface, n is the number of punctures and ri is the order of the ith cone point (ri finite and ≥ 2), each boundary component is constrained byΛ(G) of a Kleinian group in H3 is on the sphere at ∞, and the regular set is tiled by solids whose vertices meet Λ(G) at ∞ (the surface tiles we discussed above are the faces of the solid tiles where they meet the sphere at ∞). If the solid tiles of a Kleinian group only touch the sphere at ∞ at ideal vertices, Λ(G) is the entire sphere. The figure 8 knot complement is an example of such a group; the solid tiles have infinitely many sides. (Mumford et. al., ch. 12)
2 g + n - 2 + Σ (1 - 1 / ri) > 0 (see area formula above).
If G has no elliptic elements (as we will usually assume), 3g + n -3 ≥ 1, and the deformation (Teichmuller) space has complex dimension 3g + n - 3. The boundary surfaces have finite area 2π (2g + n - 2) > 0, so the boundary components can be:- a sphere with 3 or more punctures,
- a torus with at least 1 puncture, or
- any higher-genus Riemann surface with zero or more punctures.
If G has N generators, Σ gi ≤ N. If G is purely loxodromic, ∂M(G) has ≤ N/2 components.
Every closed geodesic in M(G) is the projection of a loxodromic axis (connecting the fixed points of the loxodromic element) which is independent of any elliptic elements of G.
The fixed point of a parabolic map is on the sphere at ∞. There are an infinite number of horospheres tangent to the fixed point which are left invariant by the map. A horoball is the union of a horosphere with its interior.
The projections of the universal horoballs of the group G into M(G) are mutually disjoint; there is one for each parabolic fixed point.
If the fixed point is not also fixed by an elliptic map, its stablizer is either cyclic or abelian with rank 2. If cyclic, the quotient of H3 by the stablizer is homeomorphic to a solid cusp cylinder (a solid infinitely long cylinder with its axis removed). If rank 2, the quotient is homeomorphic to a solid cusp torus (a solid torus with its core curve removed, having finite volume and surface area). The boundary of either surface is incompressible.π1 of the cusp torus injects into π1(M).
The (mutually disjoint) ε-thin parts of M are disjoint from the universal horoballs and are eitherThe process of Dehn-filling a cusp of a finite-volume hyperbolic manifold described above follows the removal of the interior of a solid cusp torus. The removal gives M a torus boundary component but does not change π1(M).
Think of the construction of the figure 8 knot complement; the removal of the vertex (necessary to make the object a manifold) removes the core curve of the torus, making it a solid cusp torus. The knot (in general, link) is the removed axis of the solid cusp torus (in general, tori).
A solid pairing tube is a finite cylinder with its axis removed, joining small discs around two punctures associated with a rank one cusp. (Think of a pairing tube as a "pinch" joining two ε-thick parts of M, with the pinch stretched out slightly so that each puncture is on one thick part.)
- tubular neighborhoods of short geodesics,
- solid cusp cylinders associated with rank 1 cusps or
- solid cusp tori associated with rank 2 cusps.
M is geometrically finite iff it is compact except for a finite number of cusps, and any rank 1 cusps correspond to pairs of punctures, each determining a solid pairing tube.
If the volume of M is finite, Λ(G) is S2, ∂M is empty, there are no rank 1 cusps and at most a finite number of rank 2 cusps.
M does not contain any essential annuli. (Purcell, p. 153)
- If M is geometrically finite, 0 < dim(Λ) < 2.
- If Λ is an S1, dim(Λ) = 1.
- If Λ is a quasicircle, dim(Λ) > 1.
- If Λ is totally disconnected, dim(Λ) < 1.
- For a singly degenerate G (which is geometrically infinite), dim(Λ) = 2.
(Series, p. 1, 2, 5, 7) (Marden, sections 2.2, 2.3, 3.1 - 3.4, 3.6, problem 3.20, 4.9, 4.10)
- A Geodesic Lamination Λ is a subset of H2 containing a closed set
of mutually disjoint geodesics. Each component is called a leaf; two leaves may have a
common endpoint on ∂H2, but no leaf can end at a puncture.
The components of H2 - Λ are called
gaps and are ideal polygons; if there are no punctures, the gaps are ideal triangles.
The projection of a measured lamination Λ to R = H2 / G is a set of simple closed geodesics. The space formed by projecting out scalar multiplication is homeomorphic to S6g+2n-7 (for n punctures). That projective space is the boundary of the Teichmuller space of R; the resulting closure is homeomorphic to B6g+2n-6.
(Marden, sections 3.9, 5.11)
-
If E2 is the sphere at ∞ of H3, the
convex hull boundary of G is the smallest convex set in
H3 which meets ∞ in Λ(G). It is the union of hemispheres whose
(B2) boundaries contain Ω(G) and intersect Λ(G) in at
least 3 points.
(Mumford et. al., ch. 12)
The quotient of the convex hull by G is called the convex core of M(G). It is a subset of the interior of M. Every closed geodesic in M(G) lies in the convex core (the convex core is the smallest convex set containing all closed geodesics of M(G)).
The boundary components of the convex core are incompressible iff Λ(G) is connected.
The convex core has finite volume iff G is geometrically finite. If G is geometrically finite without rank 1 cusps, all rank two cusps have solid cusp tori contained in the convex core.(Marden, section 3.11)
-
The compact core of a hyperbolic manifold M(G) with G finitely
generated is a compact, connected submanifold of the interior of M(G)
whose fundamental group is isomorphic to π1(M(G))
and whose boundary components are the full boundaries of noncompact components of the
interior of M(G). For a given M(G), all compact cores are isomorphic.
M(G) can be separated into a "non-cuspidal part" Mnc(G) and a finite set of solid cusp cylinders and solid cusp tori. The ∂Mnc(G) is either a component of ∂M(G) or a doubly infinite cusp cylinder or a cusp torus.
(Marden, section 3.12)The relative compact core Crel is defined similarly to the compact core, but has additional boundary components: a closed incompressible annulus which intersects each solid cusp cylinder, and the (also incompressible) cusp tori.
π1(Crel) is isomorphic to π1(M).
- Mostow rigidity implies that if hyperbolic manifolds of finite volume (n ≥ 3) M(G) and M(H) are diffeomorphic, then there is an isomorphism relating G and H. (Marden, section 3.13)
-
An end of M(G) corresponds to an ideal boundary component
(on the sphere at ∞) of the compact
core of M(G). A relative end of M(G) corresponds to a non-annulus
boundary component of the relative compact core of M(G). Thus M can be decomposed into a
compact core and a set of ends.
And end of M(G) (or Mnc) is geometrically finite if it has a neighborhood which does not intersect the convex core of M(G). Otherwise, it is geometrically infinite, and the convex core extends into the end.
(Marden, section 5.5)
- All hyperbolic manifolds M(G) (with G finitely generated) are tame: the interior of M(G) is homeomorphic to the interior of a compact manifold, and every (relative) end has a neighborhood V which is homeomorphic to S ⊗ [0,∞) where S is ∂V (S is essentially the shape of the end at ∞). There are no simple loops in ∂M(G) which bound an essential disc in the interior of M(G). (Marden, section 5.6)
- An ending lamination is a (unique) geodesic lamination of S whose geodesics "exit" the (∞) end. Every simple closed geodesic in S crosses the lamination. Any geometrically infinite end is completely characterized by its ending lamination. (Marden, section 5.7)
-
The hyperbolic Laplace-Beltrami operator in the unit ball model is
Δhu = ((1 - r2)2 / 4) (Δu + (2r/(1 - r2)) ∂u/∂r,
where Δu is the Euclidean laplacian.If G is nonelementary and M(G) has infinite volume,
- λ0 = 0 and d = 2 iff G is geometrically infinite,
- λ0 = 1 iff G is geometrically finite and d ≤ 1, and
- 0 < λ0 = d(2-d) < 1 iff G is geometrically finite and 1 < d < 2,
where λ0 is the lowest eigenvalue of the hyperbolic Laplace-Beltrami operator on M(G) and d is the Hausdorff dimension of Λ(G) of G. (Marden, section 5.15)
-
To summarize:
- A hyperbolic manifold M can be constructed as the quotient of H3 by a Kleinian group G (which is discrete, and we will assume it has no elliptic elements). Its limit set Λ(G) lies on the S2 at ∞.
- If G has n generators and no parabolic elements, Λ(G) is totally disconnected, and the quotient ∂M(G) of its regular set Ω(G) by G is a Riemann surface of genus n (possibly with twists).
- Such a surface has 3g-3 loops (which divide ∂M(G) into 2g-2 pairs of pants) which can be pinched by parabolic elements in G. Each parabolic element generates a cusp puncture in ∂M(G) corresponding to a solid pairing tube.
- When Λ(G) is a quasicircle, for each additional equivalence class of parabolic elements, one component of Ω(G) will break up into an infinite set of tangent discs.
- Non-degenerate groups are geometrically finite.
- Each degenerate component of Ω(G) has zero area (it is filled by Λ(G), which has dimension 2).
- If G is maximally degenerate, all of Ω(G) has zero area and Λ(G) is the S2 at ∞.
- Each cusp in a degenerate group corresponds to either a solid cusp cylinder (for a rank 1 cusp, which makes the volume of M infinite), or a solid cusp torus (for a rank 2 cusp, which makes M geometrically infinite but with finite volume).
- Each solid pairing tube is characterized by a (homotopy) winding number.
- Each solid cusp torus is characterized by a pair of winding numbers (for each homotopy generator of the torus).
- Each degenerate end of M(G) corresponding to a solid cusp cylinder is characterized by its ending lamination, which can be thought of as the irrational winding number of the infinite end.
- π1 of each cusp injects into π1(M(G)).
- Further manifolds can be created by Dehn filling solid cusp tori.
Orbifolds
An orbifold is a Hausdorff space M which is the quotient of a geometric space X by a discrete subgroup Γ of the similarities of X which do not necessarily act freely (Γ contains elliptic elements). In particular:- If a cone angle is irrational, Γ is not discrete and the object is then called a cone manifold.
- Tha analog of the covering map is the developing map, which "unrolls" the orbifold in H3. The corresponding holonomy map sends π1((M - cone axes) / elliptical elements) to the group of Moebius transformations generated by the elliptical elements.
- If two cone manifolds are homeomorphic with corresponding cone angles equal (and at most π), the two manifolds are isometric.
- A singular point is a point whose stabilizer is of order > 1.
- If X is Sn, Rn or Hn, X / Γ and X / Κ are isometric iff Γ and Κ are conjugate in the isometry group of X.
- The link of a cusp point of a complete hyperbolic 3-orbifold has trivial holonomy.
- Dehn surgery invariants of a hyperbolic 3-orbifold need not be relatively prime (d is the greatest common divisor).
- A complete 3-orbifold is homeomorphic to a manifold obtained from (p/d, q/d) Dehn surgery on a knot complement.
- A 3-orbifold is topologically a manifold; higher dimensional orbifolds are not necessarily manifolds.
On Knots
If you're going to play with knots, I recommend building a jig; tying knots without something to hold the crossovers in place can be very difficult. I simply cut a square piece of laminate and hammered 25 nails into it. Knot 63 (from the standard tables) is shown here:
- S1 is the unknot.
The crossing number of a knot is the minimum number of crossings for all planar projections of the knot. It is an isotopy invariant.
An isotopy is a homotopy between embeddings (making it a homeomorphism).
For an oriented link, we can assign a value to each crossing of different components:
The linking number is half of the sum of those crossing numbers, and is also an isotopy invariant.- +1 if rotating the overstrand in a counterclockwise direction will align it with the understrand;
- -1 if rotating the overstrand in a clockwise direction will align it with the understrand.
For a projection of an oriented link, the writhe is the sum of the crossing numbers for all crossings. It is not an isotopy invariant.
A knot which can be separated into nontrivial sub-knots, each of which can be enclosed in a sphere intersected by only two arcs, is composite (denoted as K1 # K2). If such a decomposition is not possible, the knot is prime.
The number of prime knots with each crossing number up to 15 have been computed:
A knot which is isotopically equivalent to its mirror image is amphicheiral.3 4 5 6 7 8 9 10 11 12 13 14 15 1 1 2 3 7 21 49 165 552 2176 9988 46972 253293 Of the knots up to 9 crossings, the only achiral knots are 31, 63, 83, 89, 812, 817 and 818.
A sub-knot whose planar projection intersects a surrounding circle four times is a tangle.A knot formed by rotation or inversion of a tangle is a mutant.
An alternating knot is a knot whose crossing signs alternate as the knot is traversed in a given direction.
A knot which can be invertibly mapped to the surface of a torus is a torus knot.
A (p,q)-torus knot wraps around the meridian p times and around the longitude q times. A (9,2) torus knot:

If a knot is embedded in an unknotted solid torus, and that solid torus is then knotted, the resultant embedded knot is a satellite knot. (Adams, pp. 2-3, 8-9, 15, 19, 41, 49, 108, 115, 152) (Lickorish, p. 6)
A connected sum (composite) knot is always a satellite knot. (Purcell, p.15)
A prime alternating knot is either a (2,q)-torus knot or is hyperbolic. (Purcell, p.230) - If K1 # K2 is an alternating knot, their crossing numbers are simply additive. (Adams, p. 69)
- A (p,q)-torus knot is also a (q,p)-torus knot.
The crossing number for a (p,q)-torus knot is min (p (q - 1), q (p - 1)). (Adams, pp. 110-111)
- A (p,q)-torus knot can be parametrized on a torus of radius 1/4 by
- x(t) = cos (p t) + cos (p t) cos (q t ) / 4
- y(t) = sin (p t) + sin ( p t) cos ( q t) / 4
- z(t) = sin ( q t) / 4
There are similar expansions for Lissajous knots and the knots 31, 41, 51 and 819. (Kauffman (Fourier), p. 366) (Trautwein, pp. 355-356, 359, 361)
- Torus knots and satellite knots are not hyperbolic. All other knots are.
A hyperbolic knot is a knot whose complement can be given a metric of constant curvature -1.
(Adams, pp. 119-120) - If two knot complements share an orientation-preserving homomorphism, the knots are equivalent. (Purcell, p. 2)
Polynomials
- The HOMFLY polynomial P(l,m) is defined by the following skein relations between three links L+,
L- and L0, which differ by only one crossing:
- Punknot = 1
- l PL+ + l-1 PL- + m PL0 = 0
PL for an arbitrary link is constructed recursively from polynomials for simpler links.
PL is an isotopy invariant. (Lickorish, p. 168)
- Pdisjoint union of L1 and L2 = -(l + l-1) m-1 PL1
PL2
PL1 # L2 = PL1 PL2
PL is unchanged by mutation of L.
PL is invariant under reversal of orientation of all components. (Lickorish, p. 179, 180)
- The Jones polynomial VL (t) = PL (i t-1, i (t-1/2 - t1/2).
The Alexander polynomial ΔL (t) = PL (i, i (t1/2 - t-1/2). (Lickorish, p. 180)
- If U is the 0-crossing planar projection of the unknot, and defining the following diagrams:
The Kauffman polynomial F(a,z) = a- writhe Λ (a,z) is defined by the following skein relations:
- ΛU = 1
- ΛL = a Λ0
- ΛD+ + ΛD- = z (ΛD0 + ΛD&infin)
F(a,z) is an isotopy invariant independent of P(l,m). (Lickorish, p. 174)
-
Fdisjoint union of L1 and L2 = ((a + a-1) z-1 - 1) FL1 FL2
FL1 # L2 = FL1 FL2
FL is unchanged by mutation of L.
FL is invariant under reversal of orientation of all components. (Lickorish, p. 179, 180)
References
- Abikoff, W., "Kleinian groups - geometrically finite and geometrically perverse", in Geometry of Group Representations, AMS (1988)
- Adams, C. C., The Knot Book, AMS (2001)
- Adams, C., Hildebrand, M. and Weeks, J., "Hyperbolic Invariants of Knots and Links", Trans. of the AMS 326 (1991)
- Alexandroff, P., Elementary Concepts of Topology, (1932), Dover (1961)
- Anderson, M. T., "Geometrization of 3-Manifolds via the Ricci Flow", Notices of the AMS 51 184-193 (2004)
- Averett, M., "An introduction to the classification of manifolds, with the Poincare conjecture as an example"
- Besse, A. L., Einstein Manifolds, Springer (1987)
- Borisenko, A., "An Introduction to Hamilton and Perelman's work on the conjectures of Poincare and Thurston"
- Bott, R. and Tu, L. W., Differential Forms in Algebraic Topology, Springer (1982)
- Callahan, P. J., Hildebrand, M. V. and Weeks, J. R., "A Census of Cusped Hyperbolic 3-manifolds", Mathematics of Computation 68 321-332 (1999)
- Christenson, C. O. and Voxman, W. L., Aspects of Topology, Marcel Dekker (1977)
- Coulson, D., Goodman, O., Hodgson, C. and Neumann, W., "Computing Arithmetic Invariants of 3-Manifolds", Experimental Mathematics 9 127-152 (2000)
- Dunfield, N. M. and Thurston, W. P., "The virtual Haken conjecture: Experiments and examples", Geometry and Topology 7 399-441 (2003)
- Edelsbrunner, H. and Harer, J., Computational Topology: An Introduction (2008)
- Eguchi, T., Gilkey, P. B. and Hanson, A. J., "Gravitation, Gauge Theories and Differential Geometry", Physics Reports 66 213-393 (1980)
- Gabai, D., Meyerhoff, R. and Milley, P., "Mom technology and volumes of hyperbolic 3-manifolds", "Minimum volume cusped hyperbolic three-manifolds", and Meyerhoff, R. and Milley, P., "Minimum volume hyperbolic 3-manifolds", in preparation.
- Goldberg, S. I., Curvature and Homology, (1962), Dover (1982)
- Gray, B., Homotopy Theory, Academic Press (1975)
- Greenberg, M. J. and Harper, J. R., Algebraic Topology, a First Course, Revised, Benjamin Cummings (1981)
- Gukov, S., "Three-Dimensional Quantum Gravity, Chern-Simons Theory, And the A-Polynomial"
- Haskins, C. N., "On the Invariants of Quadratic Differential Forms", Transactions of the American Mathematical Society 3, 71-91 (1902)
- Henle, M., A Combinatorial Introduction to Topology, W. H. Freeman (1979)
- Hilden, H. M., Lozano, M. T. and Montesinos, J. M., "The Whitehead Link, The Borromean Rings and the Knot 946 are Universal", Collect. Math. 34, 19-28 (1983)
- Hilden, H. M., Lozano, M. T. and Montesinos, J. M., "On Knots That Are Universal", Topology 24, 488-504 (1985)
- Hirsch, M. W., Differential Topology, Springer (1976)
- Hodgson, C., Issa, A. and Segerman, H., "Non-geometric veering triangulations", arXiv.org/math:1406.6439 (2014)
- Hu, S.-T., Homotopy Theory, Academic Press (1959)
- Karlhede, A., "A Review of the Geometrical Equivalence of Metrics in General Relativity", General Relativity and Gravitation 12, 693-707 (1980)
- Kauffman, L. H., On Knots, Princeton (1987)
- Kauffman, L. H., "Fourier Knots", in Ideal Knots, World Scientific (1998)
- Koehler, K. R., Computations in Riemann Geometry (2005)
- Koehler, K. R., "Drifting in and out of Teichmuller Space" (2020)
- Kramer, D., Stephani, H., Herlt, H. and MacCallum, M., Exact Solutions of Einstein's Field Equations, Cambridge (1980)
- Lickorish, W. B. R., An Introduction to Knot Theory, Springer (1997)
- Lyndon, R. C. and Ullman, J. L., "Groups Generated By Two Parabolic Linear Fractional Transformations", Canadian Journal of Mathematics 21 1388-1403 (1969)
- Marden, A., Hyperbolic Manifolds, Cambridge (2016)
- Meyerhoff, R., "Geometric Invariants for 3-Manifolds", The Mathematical Intelligencer 14 37-53 (1992)
- Milnor, J. W. and Stasheff, J. D., Characteristic Classes, Princeton (1974)
- Mumford, D., Series, C. and Wright, D., Indra's Pearls, Cambridge (2008)
- Neumann, W., "Extended Bloch group and the Cheeger-Chern-Simons class", Geometry and Topology 8 413-474 (2004)
- Percell, J. Hyperbolic Knot Theory (2010)
- Ratcliffe, J. G., Foundations of Hyperbolic Manifolds, Springer (2006)
- Sakuma, M. and Weeks, J., "Examples of canonical decompositions of hyperbolic link complements", Japanese Journal of Mathematics 21 393-439 (1995)
- Scott, P., "The Geometries of 3-manifolds", Bulletin of the London Mathematical Society 15 401-487 (1983)
- Series, C., "A Crash Course on Kleinian Groups", ICTP Trieste, June 2005
- SnapPy, by Culler, M. and Dunfield, N., a Python interface to SnapPea, by Weeks, J.
- Takahashi,M., "On the Concrete Construction of Hyperbolic Structure of 3-manifords", Tsukuba Journal of Mathematics 9 41-83 (1985)
- Tao, T., "Compactness and Compactification" (preprint)
- Thurston, W. P., Notes: "The Geometry and Topology of Three-Manifolds"
- Thurston, W. P., Three-Dimensional Geometry and Topology, Princeton (1997)
- Thurston, W. P., "How to See 3-manifolds", Classical and Quantum Gravity 15 2545-2571 (1998)
- Trautwein, A. K., "An Introduction to Harmonic Knots", in Ideal Knots, World Scientific (1998)
- Wald, R. M., General Relativity, Chicago (1984)
- Weeks, J., "Computation of Hyperbolic Structures in Knot Theory", in Handbook of Knot Theory, Elsevier (2005)
- Weeks, J., The Shape of Space, 2nd ed., CRC Press (2002)
- Yokota, Y., "On the cusp shape of hyperbolic knots", Journal of Knot Theory and Its Ramifications 25,5 World Scientific (2016)
©2022, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
- if G is a parabolic group of rank two (a and b are both parabolic) operating on mutually tangent paired curves (as below) with Tr(abAB) = -2, ∂M is a surface of genus two with three punctures, equivalent to a pair of triply-punctured spheres: