Algebraic Computation without Mathematica

The only real purpose of programming algebraic computations in a traditional language is efficiency. As noted previously, tensor operations involving large numbers of contractions do not scale well in a truly general-purpose environment such as that provided by Mathematica. We begin then by narrowing the scope of what we intend to accomplish to something that can be represented and manipulated easily and quickly.

As an example, consider the Kerr-Newman Metric. It can be parameterized as

g_{r r} = -f / (2 h r)
g_{θ θ} = -f / q
g_{φ φ} = -a⁴ q / f + 2 a² h q² r / f -
2 a² q r² / f - q r⁴ / f
g_{φ t} = a e² q / f - 2 a M q r / f
g_{t t} = -a² c² / f - e² / f + 2 M r / f - r² / f

with

f = a² c² + r²
h = (a² + e² + r (-2 M + r)) / (-2 r)
q = c² - 1

By reducing the class of problems of interest to those that can be represented as polynomials with real coefficients and integer exponents, we

simplify the storage and multiplication of terms, and parameterization functions and their derivatives can be pre-computed for easy chain-rule differentiation;

make most computations integer, which are far faster than floating point;

reduce memory requirements by the sparse storage of terms on linked lists (the lists are doubly-linked to facilitate insertion and removal).

This approach has several potential problems:

The parameterization of fractional exponents can be awkward, but is tractable:
1 / ( 1 + k / r³ ) ^{( 1 / n )} = 1 / q ->
qⁿ = 1 + k / r³

so that, for instance,
n q ^{( n - 1 )} dq / dr = - 3 k / r⁴
and
dq / dr = - 3 k / ( n q^{( n - 1 )} r⁴ )

Constants must be handled as such: a, M, e, I need to have zero derivatives.

Recurring fractions are most efficiently handled through the definition of additional constants; this also reduces floating point representational error.

Ansatze are also awkward: if u(r) is not known at computation time, neither are its derivatives, so we parametrize them as well:
u'(r) = v(r) and
u''(r) = w(r)
Only two derivatives are needed as long as any computations only involve the Christoffel Symbols and the various curvature tensors.

Implementation in C or C++

What follows is a series of suggestions, most of which apply to any programming project.

Sanity checks are an important part of any algorithm, especially one as general as we are attempting:

Class members should be protected as much as possible.

All unused or freed pointers should be set to NULL.

Make sure classes or structures are unlinked from lists before freeing or deleting them.

Abort on any unsuccessful malloc or new.

Use magic numbers for each class or structure, and check them at each reference. Invert them when the structure is freed (A magic number is a unique constant identifier for each structure type).

All indices should be checked for bounds violations before using them.

Inter-process message tracing is necessary for debugging sequencing problems.

Use
#ifdef debug
to allow some sanity checking to be easily turned off when the application is "stable".

A number of optimizations are also possible:

Inlines can be used to speed procedure calls, although they can make debuggers crazy.

Check for factors of 1 or 0 to avoid unnecessary computation.

Free all unused memory as soon as possible.

Linked lists are good for processing nonzero components, but lookups are expensive even with good hashing. For that reason, maintain a non-sparse array for each tensor with pointers to components to enable fast location of a component with specified indices.

When raising or lowering flat-space lorentz indices, use the fact that the operation only reverses the sign of timelike indices and leaves the others unchanged.

Precompute (once) and keep ε matrices in memory (make sure that their sum is zero to check consistency). ε components can be stored as
(index value) << (4 * index number) + ((value < 0) ? 1 << 50 : 0) in long longs.

If you are only contracting ε symbols with antisymmetric indices in pairs, you will need 2^{D / 2} fewer components (the consistency sum should now equal (D/2)!).

Gamma matrices (and their antisymmetric products) can likewise be precomputed, but you need to differentiate tensor and spinor indices, and allow for values of +- I:
((spinor index) ? (index value) << (4 * number of spacetime indices + 8 * spinor index number) :
(index value) << (4 * spacetime index number)) +
((value < 0) ? 1 << 50 : 0) + ((value = +- I) ? 1 << 51 : 0)

Software metrics are also a very good idea for any algorithm of this complexity:

Record the number of entries into procedures and execution timings for long operations.
Keep track of the maximum depths of hash overflows or searched linked lists.

Classes used in PTAH

A good set of data structures will make any program easier to code and debug. It is for this reason that C++ was chosen as the implementation language for PTAH (whose predecessor was written in C). The following classes are used in PTAH:

term:

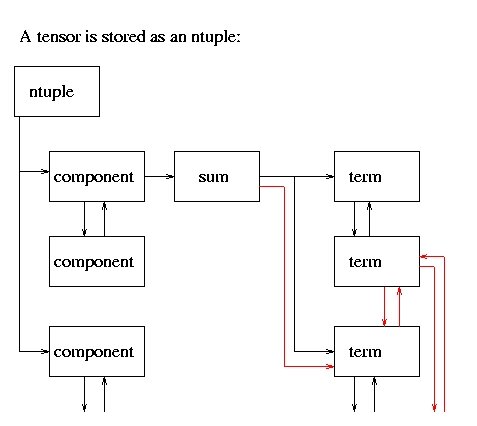
term contains

a long long coefficient and
an array of integer exponents, one for each coordinate, parameterization function, ansatz, constant and fraction denominator (like halves, thirds, etc.).
Before adding terms, one must be sure that all powers, including those of fractions, are identical, and
before storing terms, one must cancel common factors of fractions with the coefficient (ie., 6 * 2^-1 should be replaced by 3 * 2⁰).

term is a subclass of element, which are linked into hash lists (see below).

sum:
A sum is a linked list of terms, each with a unique set of exponents. (ie., 2 r³ a + 3 r³ a should be stored as 5 r³ a). The list is actually split into an array of lists, and the exponents are hashed to select a particular list in the array on which to store any given term. During the development of PTAH, we chanced upon a novel hash algorithm which reduced collision frequency by O(10):
inline void hash_code (int* factor_powers_param) {
long product = size;
for (int i = 0; i < rank; i++) {
last_hash = factor_powers_param[i] * (i + 1) * ((int) variables[i]);
product = (product | last_hash) - (product & last_hash);}
last_hash = labs (product) % size; }

The hash size is in general a prime number (PTAH currently uses 293). Of course, when a collision occurs (two terms hashing into the same list), the list is searched linearly.
sum is a subclass of hash, where all operations involving linked list traversal, insertion and removal are collected.
Simplification of sums requires a little work. For instance,
if p = r² + a², we would like
( r⁴ + 2 a² r² + a⁴ ) / p³ -> 1 / p
We have found that polynomial division is most effective when simplifying from high to low values of the exponents, so:
- each parameterization function has an associated "sort" variable or constant;
- terms are sorted from the highest to lowest power of that variable;
- during simplification, each term is on one sort list for each function; all terms are placed over the greatest common denominator and all occurences of each function in the numerator are expanded; then for each function, we attempt to divide out all possible powers of the function.
Simplification has not proven very easy or effective, and is not used on scalar invariants during parallel runs because output is currently only collected at the end.
The sum class contains methods to zero, assign, search for, add and multiply sums, and to take partial derivatives, simplify and output sums.

component:
component is another subclass of element. Component indices are packed into a 64 bit quantity for faster comparison, as in the ε example above. This currently limits us to D = 12 and index values from 0 to 62. Just as there must only be one term in a sum with a particular set of exponents, there must only be one component with any given set of indices.
component contains a pointer to a sum, which in turn represents the value of that component.

ntuple:
ntuple is a subclass of hash, with components as elements. ntuple contains
the tensor rank,
flags for upper, antisymmetric (in pairs), symmetric (in pairs) and spinor indices (PTAH uses symmetry to avoid unnecessary computation, as in the previous Mathematica examples), and
a flag for metric tensors so the contraction process knows the final index structure; ie., we want
g^{a b}T_{b c} = T^a_c,
not T_c^a.

ntuple contains methods for sum-type operations, plus methods to raise and lower indices, contract indices, transpose indices, use symmetry to add components, take covariant derivative and compute the dual of a tensor.

These classes are connected as follows:

The red arrows indicate the links for the sort lists used during simplification.

PVM - Parallel Virtual Machine

PVM is the underlying MIMD cluster software chosen for PTAH. It was chosen primarily because it provides tools to build in fault tolerance. PVM provides procedures for interrogating the cluster configuration, spawning tasks, sending and receiving messages (both data and control) between tasks and providing notification when a task dies. PVM does not guarantee message ordering, so that must be done by hand.

Hybridization with Mathematica

PTAH provides Mathematica functions to write C++ header files for the exportation of tensors and parameters. C++ procedures in PTAH then build sums and ntuples from the information in the header files. PTAH output is formatted as Mathematica FullForm, providing easy importation into Mathematica for further analysis. PTAH also outputs the definition of a simplification function to replace parameterization functions by their definitions.

Here is a partial comparison of PTAH timings with Mathematica for the above analyses of Kerr^D (times are in seconds):

D Mathematica PTAH number of products computed by PTAH maximum PTAH working set (MB)

4 35 6 87328 7

5 89 17 119715 11

6 785 21 185787 18

7 1524 52 239144 28

8 5086* 106 336566 44

9 14348 309 427735 67

10 39482* 13323 827700 99

11 95367 3117 723598 142

* = does not include computation of the Euler Class due to the excessive time required

D	Mathematica	PTAH	number of products computed by PTAH	maximum PTAH working set (MB)
4	35	6	87328	7
5	89	17	119715	11
6	785	21	185787	18
7	1524	52	239144	28
8	5086*	106	336566	44
9	14348	309	427735	67
10	39482*	13323	827700	99
11	95367	3117	723598	142

These computations were performed on one 1533 MHz Athlon with 512 MB of DDR-266 RAM.

Table of Contents

Index:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Please send comments or suggestions to the author.