
| (prev) | (top) | (next) |
Think of the second factor as describing a "static standing wave", and the first factor as its time-dependent amplitude.
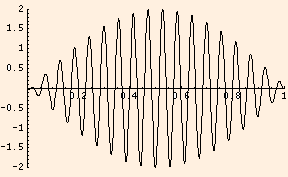
Here, the first factor describes the "envelope" and the second describes the oscillation inside; the picture shows one half of an envelope cycle,
which is heard as a single beat.
Superposition
A sin(k x - ω1 t) + A sin(k x - ω2 t + φ)
This solution, with ω2 = - ω1 (a superposition of a left mover and a right mover of equal frequency),
is a standing wave:
= 2A cos((ω1 - ω2) t / 2 + φ / 2)
sin(k x - (ω1 + ω2) t / 2 + φ / 2)
2A cos (ω1 t + φ / 2) sin (k x + φ / 2)
The value of the wave number is constrained by the boundary conditions. For a standing wave of length L:
2A cos((ω1 - ω2) t / 2 ) cos((ω1 + ω2) t / 2)
with beat frequency ω1 - ω2:
For constructive interference, the phase difference must be an even multiple of π.
For destructive interference, the phase difference must be an odd multiple of π.
| (prev) | (top) | (next) |
©2010, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.