Waves are oscillations in an elastic medium:
In all of the examples in the previous paragraph, the medium had a fixed length. This was determined by the tension in your vocal cords, the fingering of the musical instrument, the length of the air column or the distance between buildings. Waves in such a medium are called standing waves, and are sensitive to boundary conditions: whether the ends of the medium are fixed, or are allowed to freely vibrate.
If the ends of the medium are fixed at both ends, as occurs in your vocal cords, the stringed instrument or the radio waves between buildings, the wave is described by
If one end of the medium is fixed but the other is allowed to freely vibrate, as in the wind instrument, organ pipe or your nasal cavity, the wave is described by the same equation, but with
If both ends of the medium are allowed to freely vibrate, such as in your oral cavity, the wave is described by
Each value of n determines the mode of vibration:
n = 2 is the first overtone or second harmonic, etc.
For each mode, there are a number of nodes: values of x for which y is always 0. These nodes are located at integer multiples of π / k for sine waves and odd integer multiples of π / 2 k for cosine waves. For fixed boundary conditions at both ends, a wave of mode n has n + 1 nodes (counting the nodes at each end). For fixed boundary conditions at one end and free at the other, a wave of mode n has (n + 1) / 2 nodes. If the boundary conditions are free at both ends, a wave of mode n has n nodes.
For each type of wave there is a characteristic velocity
The frequency of the wave is a function of this speed, the length of the medium, the mode number and the boundary conditions. If the boundary conditions are the same at both ends, the frequency of a wave of mode n is
Since n is a free parameter in our discussion, it is obvious that a medium of a given length can oscillate at any of an infinite number of frequencies. Because our original equation for the harmonic oscillator is linear:
Linear waves are completely understood, due to their simplicity. Nonlinear waves, whose equation contains terms proportional to higher powers of x, are extremely difficult to analyze, and are at this point only partially understood. Examples of such nonlinear waves are breakers on the ocean surface or shock waves created by aircraft which exceed the speed of sound. The speed of a nonlinear wave is, perhaps obviously, a nonlinear function of the frequency, as well as of its amplitude.
This applet is a demonstration of the ideas we have discussed in this section, and should prepare you for our next set of problems. With it you can alter the boundary conditions of a string and superpose waves of differing modes and phase angles.
We are now ready to work some problems involving standing waves. You will be given the medium and its length, the type of wave and the mode number(s); from these you will compute frequencies, wavelengths and the number and locations of nodes. The wave will be graphed after you have answered the questions correctly.
The next section discusses the reflection, refraction and diffraction of traveling waves.
©2009, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
y(x,t) = A sin(kx) cos(ωt + δ),
where
k = n π / l,
n is an integer and l is the length of the medium. If the medium extends from x = 0 to x = l, the choice of sin (kx) for the x dependence guarantees that the displacement will be zero at the left end. The restriction on k does the same for the right end, by making sure that the argument of the sin function is a multiple of π at that end.
k = n π / 2 l,
where now n is restricted to be an odd integer. As before, this guarantees that the left end is fixed, but now forces the sin (kx) to be 1 or -1 at the right end, so that the cosine function determines the displacement there: this allows the right end to oscillate freely.
y(x,t) = A cos(kx) cos(ωt + δ),
where k and n are the same as when both ends are fixed. Here the choice of cos (kx) for the x dependence gives 1 at the left end, and the restriction on k means that the right end will be either 1 or -1, so that again the cos (ωt) determines the displacement and both ends may now vibrate freely.
n = 1 is called the fundamental or first harmonic,
The mode is equal to the number of half wavelengths which fit in the medium if the boundary conditions are the same at each end, or quarter wavelengths if they are different.
c = λ ν = ω / k
which is called the speed of the wave: the speed of sound (about 343 m/s in air at 20 degrees Celsius) or the speed of light (2.998 * 108 m/s in vacuum), which applies to radio waves as well.
For electromagnetic waves, c is 1 / Sqrt (μ ε). The relationship between the speed of light and the
electrical permittivity and
magnetic permeability was one of the first clues that light is an electromagnetic wave.
In the examples with which we began, the speed of the wave was quite variable: in your vocal cords and the stringed instrument, it depends on the tension and density of the medium and can be varied at will. The speed of vocal cord waves can vary from 3 to about 19 m/s; for guitar strings it is typically from 107 to 427 m/s.
νn = n c / 2 l.
If the boundary conditions are different at the ends of the medium, the frequency of a wave of mode n is
νn = n c / 4 l.
Since λ = c / ν, we see that the factor of 2 or 4 in the denominator corresponds to the half or quarter wavelengths which fit in the medium of length l. The units of ν are 1 / s, also called Hertz (abbreviated Hz).
Superposition
m a = - k x,
(where this k is the spring constant,) any superposition of waves of different modes is given by simply adding the waves together:
yn1,n2(x,t) = sin (k1x) cos (ω1t) + sin (k2x) cos (ω2t).
The following applet will play a superposition of two frequencies. The default frequency is 440 Hz, which is "concert A" below middle C.
The frequencies are adjustable from approximately four octaves below 440 (28 Hz) to four octaves about 440 (7040 Hz).
Be sure to check your speaker or headphone volume before playing the 3 second sample!
Try leaving frequency 1 at 440 and setting frequency 2 to 880; 660; 587; 550; and 528. What do you notice about these
particular superpositions? Do you recognize them? Why do you think they appeal (or not) to you as they do?
In this applet, the superposition as a function of time is
y(t) = sin (ω1 t) + sin (ω2 t),
which with the trigonometric identity
sin (a) + sin (b) = 2 cos ((a - b) / 2) sin ((a + b) / 2)
is equivalent to
y(t) = 2 cos ((ω1 - ω2) t / 2)
sin ((ω1 + ω2) t / 2).
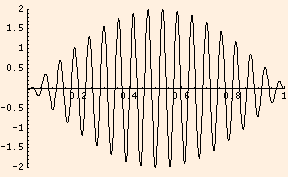
This superposed wave changes with two separate frequencies: the cosine function defines a sort of "envelope" inside of which the sine
function oscillates. The envelope amplitude has two maxima for each cycle, and these make the sine oscillation appear to waver in "beats"
with beat frequency Δ ω/2π. This waveform is a graph of a single beat: