
There are several obvious analogies between circulatory systems and electrical circuits. Current is analogous to the flow of blood, resistors dissipate energy just as viscosity does and batteries provide the energy for the movement of charge carriers in a rough analogy to the beating heart. Of course, batteries are a source of direct current, whose direction is constant corresponding to a constant potential difference. In contrast, the beating heart causes the flow of blood to be pulsatile: the blood pressure is a periodic function of time. This pulsatile flow persists throughout the arterial system, where the periodic voltage of alternating current provides a much better analogy. In the venous system, however, the flow of blood is nearly laminar, and we do not need alternating current to make our analogy with electrical circuits more precise.
We start by observing that the units of pressure are the same as the units of energy density: energy per unit volume. If we equate a volume of blood to a quantity of charge, we see that pressure is strictly analogous to voltage (energy per unit charge). The same correspondence means that flow is strictly analogous to current: volume per unit time corresponds to charge per unit time. The fluid analogy to resistance can then be seen if we solve Poiseuille's Equation for the ratio of pressure drop to flow, which is analogous to the ratio of voltage to current from Ohm's Law:
ΔP / F = 8 η l / (π r4).
The resistance of a length of wire is greater for a longer piece of wire, and less for a thicker piece of wire, just as the flow of water from a hose is less for longer hoses and greater for wider hoses. Thicker wires allow more charge carriers to flow simultaneously, while it takes more work to move the charge carriers a longer distance. This is all consistent with an equation you constructed two sections ago:
R = ρ l / A,where ρ is the resistivity, l is the length of the wire and A is its cross-sectional area. Comparing this equation to the one above, we see that if
ρ = 8 η / r2,the analogy is complete. If you have a network of veins like the following, with the pressures on the left all being (approximately) equal (a not unreasonable assumption):
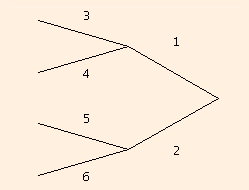
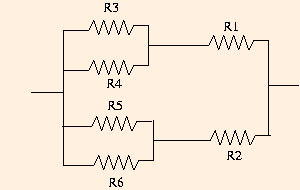
you can compute pressure drops and flows by replacing it with the electrical circuit on the right and equating currents to flows and voltage drops to pressure drops.
We can also see that Kirchhoff's Laws apply equally well to circulatory systems: if a vessel branches into two, or if two vessels join, the total flow through the two must equal the flow through the single vessel. What was conservation of charge is now conservation of matter (blood). Similarly, in a closed fluid system, the sum of the pressure drops must equal zero: the increased blood pressure at the entrance of the aorta from the heart at systole (the peak of the blood pressure increase during a heartbeat) is completely dissipated by the time the blood returns from the vena cava into the heart: the blood there is barely moving, and in fact requires help from the movement of surrounding muscles and a system of one-way valves. Of course, circulatory systems are not strictly closed: fluid can pass through the membranes of the blood vessels and, of course, the vessels themselves can be broken. But we can ignore these small and exceptional events in the analyses we are about to undertake.
In real circulatory systems, one vessel may split into two or two vessels may join into one. Hence while the entire system is a vastly complicated network of billions of vessels, flow problems ultimately come down to three vessels at a time. In this applet, you are given the characteristics of a small network of veins and will use your knowledge of electrical circuits to compute the total pressure drop and the flow through several of the veins.
It is important to recognize the limits of analogies such as the one we have drawn here between Ohm's Law and Poiseuille's Equation. When we discussed Ohm's Law, we mentioned that it
was analogous to the equation for heat conduction as well as to the one for diffusion. The physical basis for the latter
analogies is the fact that all three processes are diffusive: at their heart, they are random or stochastic processes. Molecules diffuse by random collisions, heat diffuses through
random motion of electrons and electrical current results from electron drift, which involves collisions with atoms and other electrons. But while a fluid at finite temperature does
experience thermal motion, the laminar flow described by Poiseuille's Equation is essentially a deterministic process: each "parcel" of fluid is pushed along the pipe
in largely linear motion under the influence of pressure. So while the formal analogy between Ohm's Law and Poiseuille's Equation is valid and extremely useful in solving a wide class
of problems, it is not based on common underlying physics.
The next section introduces the simple harmonic oscillator and wave kinematics.
©2013, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.