
Suppose that we repeat our diffraction experiment but only allow one photon at a time to approach the slitted surface. The applet below illustrates the results of this experiment, displaying the changing intensity as more and more photons hit the screen:
As you can see, the same interference pattern which was created by a beam of light is produced over time by the sequence of photons. Yet the existence of the interference pattern was explained by Huygens' Principle as due to each slit acting as a coherent source. This implies that each photon passed through both slits, and the resulting phase difference at any point on the screen correlates with the number of photons which eventually hit there: no photons hit where the interference is destructive, and many photons hit where the interference is constructive. Hence we conclude that traveling quanta of the electromagnetic field behave as traveling waves do.
In what is perhaps the most amazing experiment in modern physics, we find that electrons and other elementary particles do exactly the same thing! We will therefore think in terms of an electron field, made up of tiny oscillators at every point in space, just as with the electromagnetic field. This implies that a traveling electron has an associated wavelength, which we call the de Broglie wavelength:
This relationship gives us our first clue to the length scale by which particles are measured. Setting the scale using the speed of light for the velocity we find the Compton wavelength of an electron to be about 2.42 * 10-12 m, while for a proton it is 1.32 * 10-15 m. These represent minimum sizes, since velocities are always less than the speed of light.
If traveling particles share the wave characteristics of field quanta, what does this tell us about electrons bound to nuclei in an atom? Here, the appropriate model is the standing wave: it has no well-defined position or momentum, but it does have a well-defined wavelength and frequency. Consider the Hydrogen atom. Since it exists in three dimensions, we envision the electron as a sort of spherical standing wave surrounding the nucleus. Because the wave must be continuous as we travel around the sphere, we should think of it is having the same boundary conditions at both "ends". This implies that the circumference of the sphere must be equal to an integer times the wavelength:
λ = h / m v.
Bound Electrons
2 π r = n h / m v.
Rearranging this equation so that both sides have units of angular momentum, we obtain
m v r = n h / 2 π:
the angular momentum of the electron relative to the nucleus is quantized. This is known as the Bohr quantization condition.
It turns out that an electron bound to an atom has four distinct quantum numbers:
The images below are plots of the amplitude of the electron wave function for the Hydrogen atom. Because the atom is three dimensional, we have shown the intersection of the electron with the x-z plane. Each plot is labeled by the quantum numbers n, l and m; the spin quantum number does not affect the appearance of the wave function.
The first three are spherically symmetric because l is zero:
Note the nodes (black rings) in the amplitude for n = 2 and n = 3. Just as in the case of the one dimensional standing wave with fixed boundary conditions at both ends, these waves have n - 1 nodes. These electrons are called 1s, 2s and 3s, respectively, by chemists.
For nonzero l, the wave functions are no longer spherically symmetric, but pick up lobes:
These are the 1p, 2p and 3p electrons. Larger values of l produce more, narrower lobes:
These are the 3d, 4d and 4f electrons. The magnetic quantum m labels the orientation of the wave functions:
These are all 2p electrons.
The following applet will show you a full three dimensional plot of the wave function for one or two electrons in a Hydrogen atom
(for a single electron, set "n2" to zero). Push the "replot"
button to redraw the plot. The scroll bars allow you to change n, l and m for each electron. Electron 1's wave
function is plotted in magenta, and electron 2's wave function is plotted in cyan. The two colors add to blue or white where the wave
functions overlap. To change the perspective, drag the mouse across the window; to zoom, turn the scroll wheel.
This applet comes with a caveat: when plotting the wave function for two electrons, the mutual interaction of the electrons has been ignored.
This is an unfortunate necessity caused by the complexity of the equations of quantum mechanics: the applet only knows solutions in closed form for
individual electrons in a single-electron atom. But the plots still exhibit the essential qualities of the electron wave functions that interest us.
The scales appropriate to bound electrons are determined by the nature of the Coulomb attraction as well as by their mass. The length scale is set by the Bohr radius:
The average radius of a spherical electron wave function is












Please be patient: each plot requires the evaluation of each wave function at over 3.5 million points! The
"Replot" button will be labeled with ellipsis while the evaluation process is taking place.
a0 = 5.29 * 10-11 m,
which is about half an Angstrom. This value can only depend on the electrical attraction between the electron
and the nucleus, the mass of the electron, and Planck's Constant, and is derived from dimensional considerations
(see the problem below).
n2 a0 / Z,
where Z is the atomic number: the number of protons in the nucleus. The energy scale is set by the Rydberg energy:
E0 = 2.18 * 10-18 J.
This value can be derived from the sum of the kinetic energy (through the Bohr quantization condition) and the
electrical potential energy of the electron.
Physicists often express atomic energies in a more convenient unit called the electron Volt, or eV:
1 eV = 1.6 * 10-19 J,
so that
E0 = 13.6 eV.
The energy of an electron is approximately
En = - E0 Z2 / n2,
which neglects the effects of angular momentum and interactions between electrons. It essentially corresponds to an atom with an arbitrary number of protons but only one electron. The energies of electrons at various levels are negative, because they are bound. This reflects our choice of zero potential energy as corresponding to a free electron with zero velocity. As n becomes very large, the difference between two succeeding energy levels becomes vanishingly small:
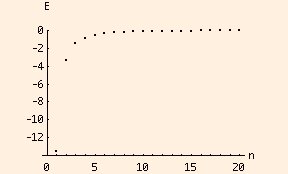
In the limit of n approaching infinity, the energy spectrum (set of levels) becomes continuous. This is called the classical limit, since classical energies are not quantized but can be any real number. A basic tenet of the quantum theory is that as n approaches infinity, the equations (ie., for energy) should become equivalent to their classical (macroscopic) counterparts. This idea is called the correspondence principle.
Is there a smallest length or a shortest time? In fact, one can construct length, mass, energy and time scales using only three fundamental constants: Newton's Constant, Planck's Constant and the speed of light. These are called the Planck length, mass, energy and time:
The Planck mass and energy are not minimums; rather, they are the mass and energy of a black hole whose size is of the order of the Planck length. A black hole is an object which has collapsed to such a massive density that even light is not fast enough to escape its gravitational attraction. Because these values involve Newton's Constant, they are relevant to Quantum Gravity: the still sought-after theory which unites quantum theory with General Relativity.
Now you have an opportunity to construct expressions for the various scales we have discussed in this section. Of particular use in some of these problems are the ratios G/c2 and e2/ε. Work out their units to figure out why they are so useful!
Notice the relationships between the Planck mass and energy, and between the Planck energy and time. These are useful in constructing energy and time scales for any particle.
For multielectron atoms, it is almost always too complicated to find exact wave function solutions; this has only been done for Hydrogen and Helium.
Instead, we must resort to approximations and numerical computer analyses. The Bohr model holds for one
electron atoms; for larger atoms, successively higher level electrons "see" successively lower values of Z due to charge screening
of the nucleus by the inner electrons. The n = 1 electrons see the actual Z, while the outermost electron of a neutral atom sees Z = 1
(assuming n is large and l is zero).
The Hartree Approximation predicts the order of electron quantum numbers which correspond to successive energy states,
taking into account charge screening and the dependence
of the energy on angular momentum (which was ignored in the Bohr model). Since larger l values indicate that more of the electron wave
function is away from the nucleus, the screening is not spherical; the order is:
The Periodic Table is based on the observation that an element's chemical properties depend on the number of electrons in its outer
(valence) shell. Without repeating quantum numbers, we can "populate" the allowable energy states using the order from the table
above, noting that for any given values of n and l, there can only be 2 * 2l +1 pairs of electrons, corresponding to the
allowable values of m and ms. For each of the pairs in the table above, you can count to see how many electrons are in the outer
unfilled shell. Elements with the same number go in the same column of the Periodic Table. When the shell is full, the element goes in the
(rightmost) "inert" column, since it does not easily react with a filled valence shell. The next element goes into the leftmost column
(for those elements with only one electron in their outer shell).
Note that the energy levels used in constructing the Periodic Table are ground states (states of minimum energy).
With sufficient energy (see the next section), any electron can "jump" to any level.
So can you never get out of a black hole no matter what you do?
To answer this question, we need to understand two new ideas: light cones and event horizons.
Every particle, at each point in its trajectory, has a future light cone and a past light cone:
A black hole is created by an object which has undergone gravitational collapse to an infinitesimal size (which means its
density approaches infinity!). The laws of General Relativity cannot predict the final state of the collapsed
object; it simply does not produce meaningful answers at those length scales. But it does predict the existence of a
boundary around the collapsed object, the event horizon, which is an imaginary surface that defines the black hole.
As anything (even light) approaches the event horizon, the gravitational attraction toward the collapsed object
becomes so great that its future light cone is tipped further and further toward the object. As it crosses the
event horizon, one direction on its future light cone is parallel to the horizon, and the rest is pointing into the
black hole. So their is NO escape once you cross the event horizon!
Let's assume for a moment that you are falling into a black hole feet first.
What you experience until you cross the horizon depends on how much mass the collapsed object has. Larger objects have horizons
which are so far away from the object that the gravitational force is essentially constant over the length of your body.
Smaller objects have horizons which are much nearer, so that the gravitational pull on your feet is much larger
than the pull on your head, resulting in significant (and perhaps fatal!) stretching.
But even if you survive to reach the horizon, regardless of the mass of the collapsed object, it's all
over. The future light cone of your feet is pointing into the center of the black hole, so no nerve impulses can
reach your head from there. When your heart crosses, no blood can flow from it to your head. And when your head
crosses the horizon, the parts of your brain cannot communicate with each other and your
consciousness ceases.
You may have heard that black holes can evaporate. While this phenomenon has not been experimentally observed, quantum mechanics
tells us that black holes can emit Hawking Radiation (named after physicist
Stephen Hawking, who first came up with this idea).
Hawking Radiation is a thermal emission which causes the collapsed object to lose mass. Eventually, the object and everything
it has swallowed disappears. But that doesn't help you if you've crossed the horizon: all of your
mass has been converted into energy and radiated off, but that thermal radiation contains none of the
structure that defined you.
There is another more important consequence of the one-way nature of the event horizon: since nothing
(except perhaps Hawking Radiation) can leave
the interior of the black hole, no information about it can ever be communicated to the outside. The interiors
of black holes are not subject to experiment! Therefore, in a very real sense, the interiors of black hole
event horizons, including the ultimate fates of the collapsed object and anything else which falls inside, lie
outside the realm of science.
In the next section we see how the transitions of electrons between energy levels is the basis for all that we see.
©2008, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.
. . .
Each of the (n, l) pairs is called an "electron shell".
In fact, the energies depend not only on n and l, but to a much smaller degree on m and ms as well,
which means the above list is only approximately correct.
n, l 1,0 2,0 - 2,1 3,0 - 3,1 4,0 - 3,2 - 4,1 5,0 - 4,2 - 5,1 6,0 - 4,3 - 5,2 - 6,1 7,0 - 5,3 - 6,2
. . .
So your future light cone contains all of your possible future paths, and your past light cone contains all that you could know
from the past.